Оглавление:




Концентрации напряжений
- Концентрация напряжений. Как мы уже видели, расчет… Расчет переменного поперечного сечения осуществляется таким же образом, как, в принципе, расчет стержней постоянного поперечного сечения, если изменение поперечного сечения достаточно плавное. Предполагается, что в поперечном сечении существуют только нормальные напряжения, они равномерно распределены. Он также предполагает, что продольное сечение параллельно оси§ 31]
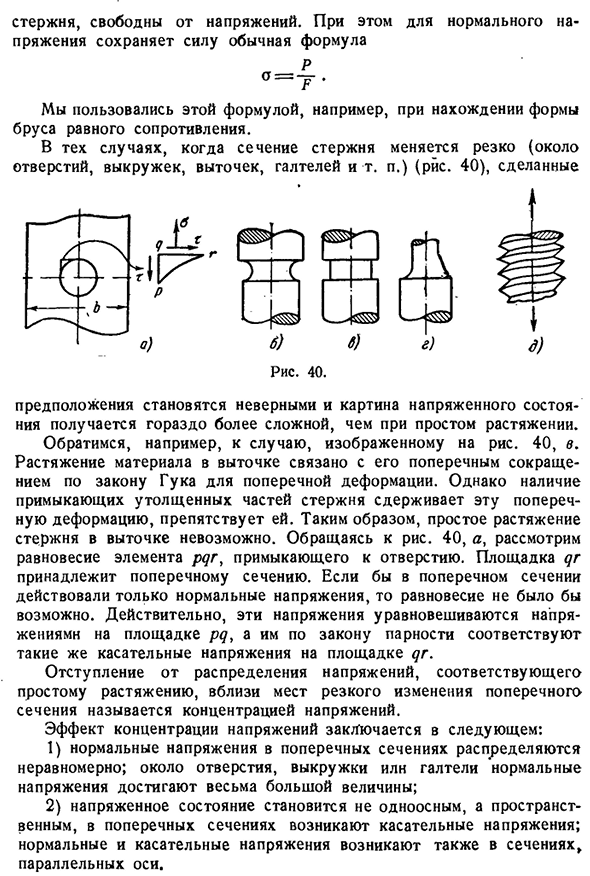
концентрация напряжений 67 Бар, свободный от давления. В то же время при нормальном напряжении, обычная формула остается в силе П A-F Например, эта формула использовалась при нахождении формы стержня равного сопротивления. В таких случаях поперечное сечение сердечника резко меняется (вокруг отверстия, скругление, подрез, скругление и др.).(Рез. 40), сделанный Предположения становятся неточными, и картина стрессовых ситуаций гораздо сложнее, чем с простыми растяжками. Обратимся, как показано на рисунке, к примеру. 40 дюймов
Натяжение материала в углублении связано с его боковой усадкой, согласно закону крюка о поперечной деформации. Людмила Фирмаль
Однако наличие соседних утолщенных частей стержня сдерживает эту поперечную деформацию и предотвращает ее. Поэтому простое растягивание стержня в углублении невозможно. Обратимся к рис. 40, а рассматривает равновесие элементов pqr, прилегающих к отверстию. QR pad принадлежит к разделу. Если в поперечном сечении имеется только нормальное напряжение, то равновесие невозможно. Фактически эти напряжения уравновешиваются напряжениями участка pq и соответствуют закону четности тех же касательных напряжений на участке qr.
Отклонение от распределения напряжений, соответствующее простому растяжению вблизи места внезапного изменения площади поперечного сечения, называется концентрацией напряжений. Влияние концентрации напряжений заключается в следующем: 1) нормальное давление поперечного сечения распределено неравномерно; вблизи отверстия нормальное давление скругления или галтеля очень велико. 3 * 68 натяжение-сжатие [Глава II Для определения закона распределения напряжений в концентрационных условиях следует отметить, что точных решений задачи полной концентрации напряжений экспериментально не существует, ни методом теории упругости, ни для модели плоских изделий из прозрачных материалов.
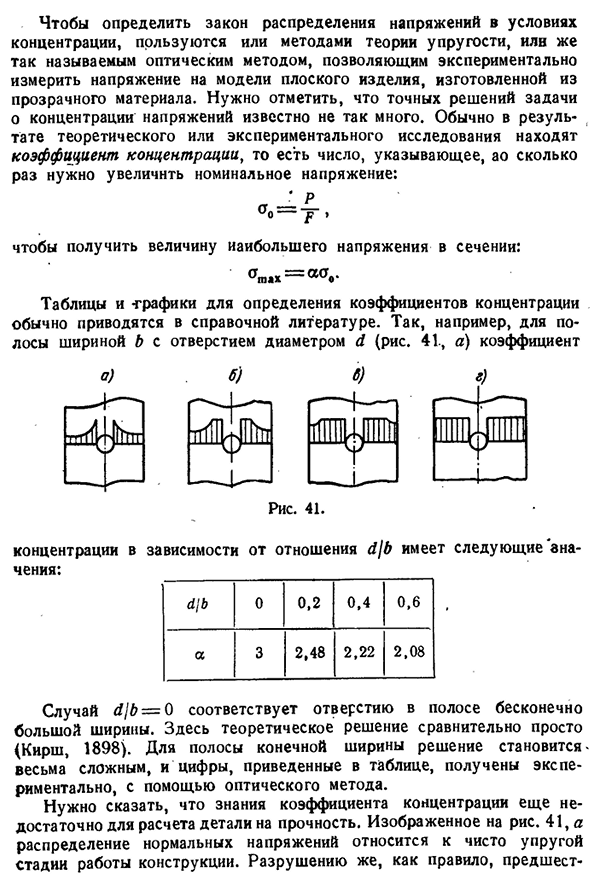
- Обычно в результате теоретических или экспериментальных исследований находят коэффициент концентрации, указывающий, во сколько раз необходимо увеличить номинальное напряжение, то есть число: Определить величину максимального напряжения в поперечном сечении: < * max=a < V таблицы и графики для определения коэффициентов концентрации обычно указываются в библиографии. Например, для полосы шириной B с отверстием диаметром d(рис. 41, а) коэффициент * 7 Если Dlb=O, то это соответствует отверстию в полосе с бесконечно широкой шириной.
Теоретическое решение здесь относительно простое (Kirsch, 1898). В случае полосы конечной ширины решение становится очень сложным, и численные значения, приведенные в таблице с использованием оптических методов, получены экспериментально. Надо сказать, что знания коэффициента концентрации недостаточно для расчета прочности детали. Как использовать 41, так и распределение нормальных напряжений относится к чисто упругой стадии строительства. Разрушение же, как правило, предварительно § 31) концентрация напряжений 69 В результате возникает пластическая деформация. Как мы увидим позже, при переменных нагрузках в упругой области может произойти разрушение, но для того, чтобы судить о прочности, знания нормального напряжения только поперечного сечения недостаточно,
поэтому принимать расчетное напряжение oft x=ao0;было бы неверно. Людмила Фирмаль
Проблема расчета прочности по концентрации требует более детального изучения и рассматривается в главе XVII. Для пластических материалов проблема прочности при концентрации напряжений также не является простой. Если перед разрушением происходит значительная пластическая деформация в месте, где напряжение считается особенно высоким, то материал переходит в пластическое состояние и образуется пластическая зона. Для ее изучения необходимо решить пространственную задачу теории пластики, что возможно лишь в небольшом числе случаев. Экспериментальный метод определения напряжений в пластической области очень сложен, и соответствующие измерения незначительны.
Поэтому первая трудность заключается в том, чтобы найти величину напряжения при переходе за предел упругости. Вторая трудность заключается в установлении критерия прочности в сложном пластическом напряженном состоянии. До сих пор мы возвращались к этим вопросам в главе XVII, где ранее рассматривались общая теория напряженных состояний и общие законы пластичности, а пока попытаемся сформулировать теорию, основанную на основном выражении. Напряжение плоскости, параллельной оси стержня, и касательное напряжение игнорируются, а напряженное состояние считается одноосным.
Если только нормальное напряжение действует в каждой точке поперечного сечения, пластическое состояние возникает, когда это напряжение равно пределу текучести. В идеальной пластичности напряжение не может быть больше Ат, поэтому дальнейший рост силы показывает упругость с увеличением напряжения остальных частей, а также диаграмму распределения напряжений по сечению, соответствующую величине силы с постоянным постепенным увеличением напряжения. Сорок один Для риса. На рисунке 41 показано распределение упругих напряжений. 41, В и 41, С-упругопластические зоны с разной степенью развития.
Как использовать 41, g показывает распределение напряжений в момент, когда полное поперечное сечение переходит в пластическое состояние. Соответствующая сила разрушительна, и ее величина: Здесь F-площадь ослабленного участка.70 растяжение-сжатие [гл. II Применяя принцип расчета допустимой нагрузки, мы создаем следующие условия прочности: Л л Но^=[a], и таким образом, Это обычная формула для расчета прочности, и концентрация напряжений в ней не отражается. Поэтому при расчете прочности стержня из пластического материала под действием статических нагрузок концентрация напряжений не учитывается.
Смотрите также:
| Напряжения при ударе | Нелинейные задачи на растяжение — сжатие |
| Распространение упругих волн в стержнях | Напряжения на косых площадках при растяжении |

