Разложение функций в степенные ряды

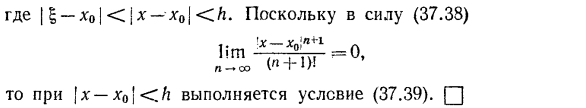
Разложение функций в степенные ряды

Разложение функций в степенные ряды. Различные способы записи остаточного числа формулы Тейлора. Определение 4.Определите функцию в окрестности x0 и получите производные всех порядков в этой точке. Затем линия называется ряд Тейлора/в x0. если x0 = 0, то ряд (37.24) также называется рядом Маклорина функции} (x). Как известно, все аналитические функции в точке x0 бесконечно дифференцируемы в некоторой окрестности этой точки, и в этой окрестности они равны сумме их Тейлора series. In в общих чертах получается, что обратное неверно. Примером такой функции является функция для χΦ0 эта функция имеет производные всех порядков, которые легко вычисляются.

Есть функции, которые не могут быть представлены в ряду Тейлора, потому что они бесконечно дифференцируемы, но не аналитичны. Людмила Фирмаль

• И вообще Где Pn (l / x) многочлен в некоторой степени относительно μ/(где n-степень многочлена, а не порядковый номер).То есть f (x) (x) это линейная комбинация терминов в виде Это может быть легко подтверждено induction. By внесение изменений、 1 уравнение в x-0(37.26). Ноги/ = 4г. Применения правила Лопиталь, чтобы найти предел упругости предел формулы x (37.26) равен нулю, n = 0, 1, 2,… из уравнения η= 0 и η= 1 (37.27) видим результат, так как функция / непрерывна в точке 1 = 0 и поэтому т/ ’(x)= 0 Раздел 11.2 теоремы 3, Часть 3) / ’ (0) существует и/’(0)= 0.By индуктивный метод, он может быть легко проверен таким же образом, как f (n) (0)= 0, n = 0, 1, 2. Итак, поскольку все члены ряда Тейлора (37.25) функции при x0 = 0 равны нулю, сумма всех x также равна нулю, и поэтому не соответствует самой функции/.

Также обратите внимание, что согласно теореме 37.3 5 функция (37.25) не может расширяться до любого степенного ряда(потому что она, по-видимому, ближе к Тейлору, если это возможно). Упражнение. 6.Is можно ли расширить функцию f (x)= e〜1 / x, x 0 в интервале[0, 1]ряда Маклорена? Поскольку мы можем определить функцию 6 (x) e〜1 / x *для x = 0, мы докажем, что в результате получаем бесконечно дифференцируемую функцию по числовой оси. Заметим, что если функция расширяется в окрестности некоторой точки степенного ряда, то такой ряд уникален(см. теорему 5 или теорему 7) и его ряд Тейлора. Однако один и тот же степенной ряд может быть рядом Тейлора различных функций. Таким образом, мощность равна нулю Коэффициент,^ Oh», подобен функции ряда Тейлора Он будет равен нулю на всей числовой оси. / (x) = 0, ряд функций Тейлора в точке x = 0(37.25).

• Это вопрос. Когда ряд Тейлора (37.24) функции f (x) сходится к f (x) на определенном интервале? Чтобы исследовать эту проблему, напишите формулу Тейлора функции/(см.§ 13.1). В этом виде он действителен для n = 0, 1, 2. Мул rn (x) указывает на остаток серии Тейлора, а не на остаток серии Тейлора. Это связано с тем, что оставшаяся часть ряда не может быть обработана до тех пор, пока не будет определено, что ряд будет сходиться-только в этом случае Косет уравнения Тейлора будет соответствовать остатку ряда Тейлора. Предположение Перепишите выражение формы (37.28) Где 8n (x) N-я частичная сумма ряда Тейлора. Это связано с тем, что функция/будет равна сумме рядов Тейлора в рассматриваемом интервале, т. е. Пз » (x)= [(x）、 Для всех x из этого интервала остаточный член в Формуле Тейлора стремится к нулю.

В этом случае из уравнения (37.29) видно, что модульный член формулы Тейлора rn (x) также является суммой M-го модуля ряда Тейлора (37.24). Теорема 8.Определите функцию/и сделайте ее непрерывной со всеми производными до N4-1, включая интервал (x0-H, x0 + H), H0.Тогда все XE (10-H, x0-{H) оставшегося члена rn (x) в этой формуле Тейлора (37.29) могут быть записаны в следующих 3 формах: Где / принадлежат интервалу, заканчивающемуся в точках x0 и x, и Уравнение (37.31) называется модулем интегральной формы Тейлора, формула (37.32) Лагранжевой формой, а формула (37.33) формой Коши. Доказательство. Из основной теоремы производной (и 29.3, см. теорему 4)、 Частичное интегрирование правого интеграла выглядит следующим образом Для некоторых из основных, мы предполагаем, что это уже доказано Частично закрепить последний срок еще раз. Замените это выражение на (37.34).

Здесь, как и выше, он находится в интервале, который заканчивается в точке x. Людмила Фирмаль

• В результате мы получили выражение (37.34), которое заменило m на m +1. Итак, формула (37.34) доказывается индукцией всех m> n. для m = n вид остаточного члена равен (37.31). Здесь мы применяем первую теорему интегрального среднего значения к интегралу (37.31) и берем производную/ («+1) вне знака интеграла » (см. результаты теоремы 28.2 1). Где|находится в интервале до конечной точки x0 и x. Формула (37.32) была доказана. Если мы применим теорему среднего значения интеграла к интегралу к интегралу (37.31) и получим среднее значение всего подынтегрального выражения по знаку интеграла (см.§ 28.2).

Смотрите также:

Предмет математический анализ

Аналитические функции.	Разложение элементарных функции в ряд Тейлора.
Действительные аналитические функции.	Множества. Операции над множествами.