Оглавление:






Классификация сверхзвуковых течений по Христиановичу
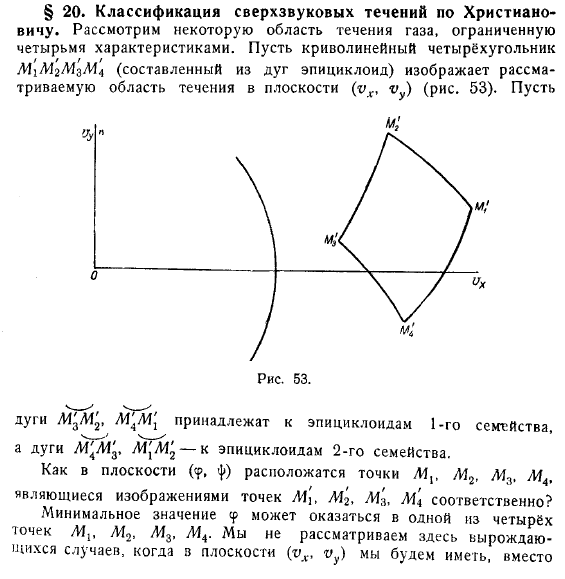
Классификация сверхзвуковых течений по Христиановичу. Рассмотрим некоторую область течения газа, ограниченную четырьмя характеристиками. Пусть криволинейный четырехугольник (составленный из дуг эпициклоид) изображает рассматриваемую область течения в плоскости (рис. 53). Пусть дуги принадлежат к эпициклоидам 1-го семейства, а дуги к эпициклоидам 2-го семейства.
Как в плоскости расположатся точки являющиеся изображениями точек соответственно? Минимальное значение может оказаться в одной из четырёх точек. Мы не рассматриваем здесь вырождающихся случаев, когда з плоскости мы будем иметь, вместо четырёхугольника, дугу характеристик 1-го или 2-го семейства. Эти случаи полностью были разобраны раньше (см. § 12). Рассмотрим все четыре возможных случая.
Смотрите также:
Решение задач по гидромеханике
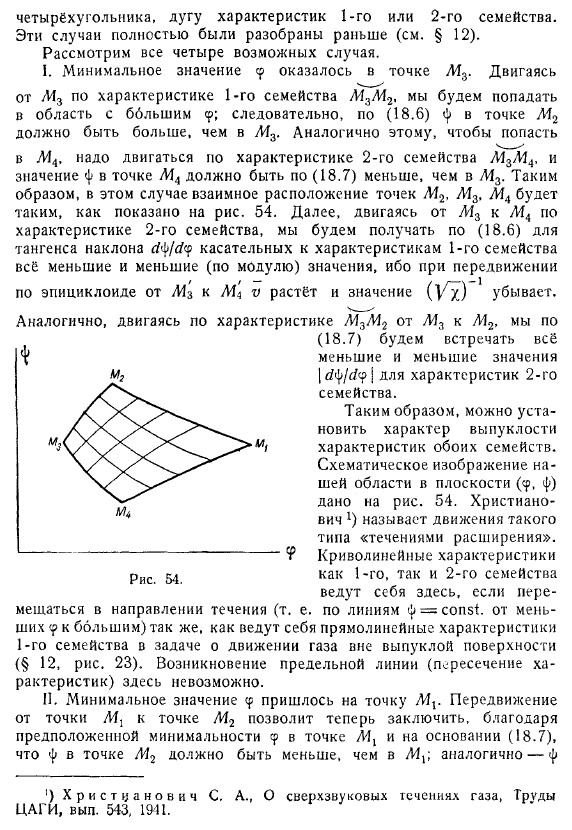
I. Минимальное значение 9 оказалось в точке. Двигаясь по характеристике 1-го семейства, мы будем попадать в область с большим ср; следовательно, по (18.6) в точке М2 должно быть больше, чем в М3. Аналогично этому, чтобы попасть в М4. Надо двигаться по характеристике 2-го семейства М3М4, и значение ф в точке М4 должно быть по (18.7) меньше, чем в М3.
Таким образом, в этом случае взаимное расположение точек М2, М3, Мл будет таким, как показано на рис. 54. Далее, двигаясь от М3 к Л14 по характеристике 2-го семейства, мы будем получать по (18.6) для тангенса наклона касательных к характеристикам 1-го семейства всё меньшие и меньшие (по модулю) значения, ибо при передвижении по эпициклоиде растёт и значение убывает. Аналогично, двигаясь по характеристике, мы по (18.7) будем встречать всё меньшие и меньшие значения для характеристик 2-го семейства.
Таким образом, можно установить характер выпуклости характеристик обоих семейств. Христианович называет движения такого типа «течениями расширения». Людмила Фирмаль
Схематическое изображение нашей области в плоскости дано на рис. 54. Криволинейные характеристики как 1-го, так и 2-го семейства ведут себя здесь, если перемещаться в направлении течения так же, как ведут себя прямолинейные характеристики 1-го семейства в задаче о движении газа вне выпуклой поверхности (§ 12, рис. 23). Возникновение предельной линии (пересечение характеристик) здесь невозможно.
Смотрите также:
Переход через скорость звука. Предельные линии. Примеры точных решений
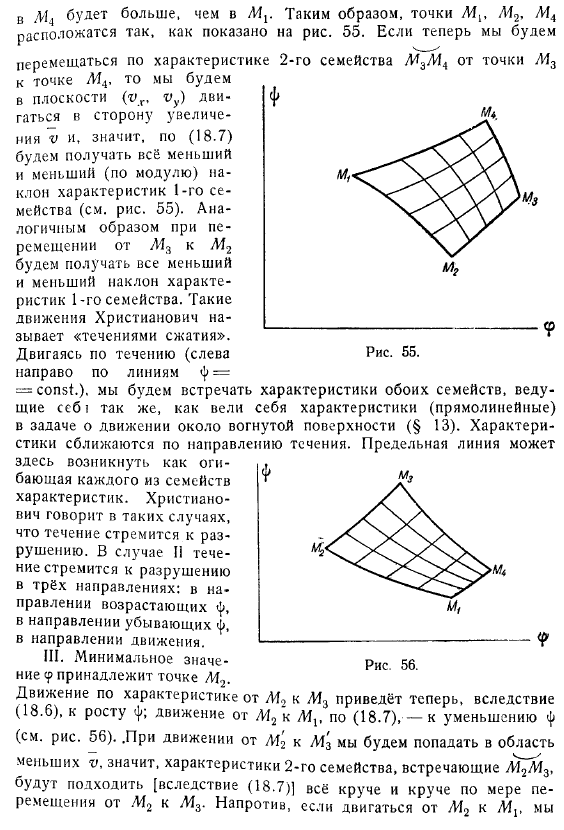
П. Минимальное значение пришлось на точку. Передвижение от точки к точке позволит теперь заключить, благодаря предположенной минимальности в точке и на основании (18.7), что в точке М2 должно быть меньше, чем в М3; аналогично для четырёхугольника, дугу характеристик 1-го или 2-го семейства. Эти случаи полностью были разобраны раньше (см. § 12). Рассмотрим все четыре возможных случая.
III. Минимальное значение ср принадлежит точке М2. Движение по характеристике от М2 к М3 приведёт теперь, вследствие (18.6), к росту; движение от М2 к М3, по (18.7) — к уменьшению (см. Рис. 56). .При движении от М2 к М3 мы будем попадать в область меньших v, значит, характеристики 2-го семейства, встречающие М2М3, будут подходить [вследствие (18.7) ] всё круче и круче по мере перемещении от М2 к М3 . Напротив, если двигаться от М2 к М3, мы будем встречать вей менее и менее наклонённые характеристики 1-го семейства .
Наконец, как и в предыдущих случаях, при перемещении по любой характеристике мы будем иметь монотонное изменение тангенса наклона этой же характеристики (неизменность знака кривизны). Такое решение стремится к разрушению в направлении убывающих, но в направлении течения оно может не претерпевать разрушения — разрыв может и не возникнуть, ввиду того, что характеристики разных семейств ведут себя здесь по-разному .Этот тип можно назвать «смешанным».
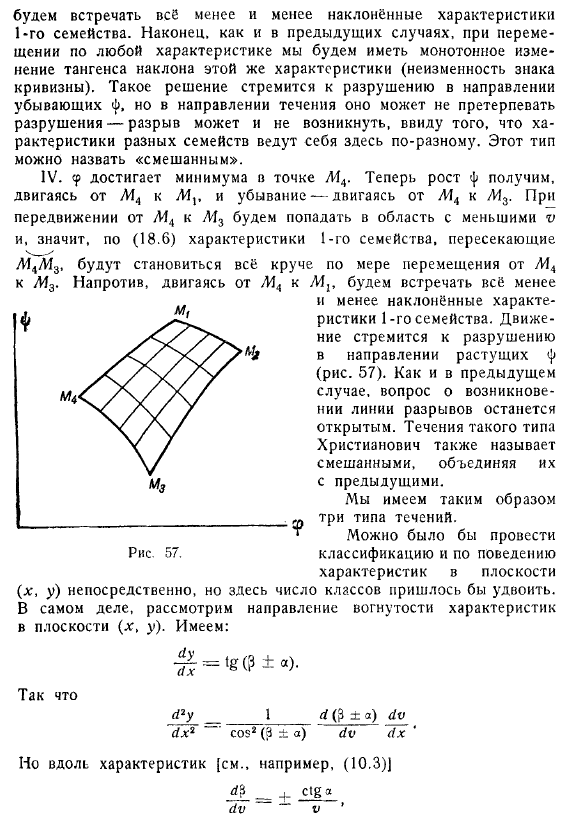
IV .ф достигает минимума в точке М4. Теперь рост ф получим, двигаясь от М4 к M1 и убывание — двигаясь от М4 к М3 .При передвижении от М4 К М3 будем попадать в область с меньшими v и значит, по (18.6) характеристики 1-го семейства, пересекающие М4М3, будут становиться всё круче по мере перемещения от М4 к М3. Напротив, двигаясь от М4 к М1, будем встречать всё менее и менее наклонённые характеристики 1-го семейства .
Движение стремится к разрушению в направлении растущих (рис . 57) .Как и в предыдущем случае, вопрос о возникновении линии разрывов останется открытым. Течения такого типа Христианович также называет смешанными, объединяя их с предыдущими. Мы имеем таким образом три типа течений. Можно было бы провести классификацию и по поведению характеристик в плоскости непосредственно, но здесь число классов пришлось бы удвоить .
Смотрите также:
В самом деле, рассмотрим направление вогнутости характеристик в плоскости (х, у) . Такие точки перегиба на характеристиках отчётливо видны, например, на рис. 49 и рис. 51 там, где наши характеристики пересекаются с линиями. Таким образом, классифицировать пришлось бы отдельно для М<М0 и М > М0.
Посмотрим теперь, к какому классу движений принадлежит движение, получающееся сразу же за «переходной линией» в сверхзвуковой области. Отправляемся на этот раз от уравнений (9.2) и условия отсутствия вихрей. Вводя величину скорости v и угол ф, так что мы можем переписать наши уравнения в виде Чтобы выяснить, что будет происходить около линии v= 1, рассмотрим сперва произвольную линию v = const.
Пусть Р — точка на этой линии. Обозначим длину, отсчитанную по луге от точки Р вдоль линии v = const, через S . Нормаль в Р к линии v — const, обозначим буквой n. Направив ось Ох по касательной, а ось Оу по нормали к линии v = const, в точке Р, мы можем переписать уравнения (20 .1). Исключив из этих уравнений, мы получили следующее равенство, связывающее .
Особенно простой вид получит формула (20.3), когда наша линия v = const, есть линия перехода. Заметим, что если нормаль направлена в сторону сверхзвуковой зоны, то будет dv/dn > 0, и таким образом db/ds > 0. Отсюда мы получаем важное следствие: если перемещаться по линии v = 1, то угол между направлением скорости и направлением касательной к линии v=1 будет меняться монотонно и именно так, что если при нашем перемещении сверхзвуковая скорость остаётся слева, то вектор скорости будет вращаться против часовой стрелки.
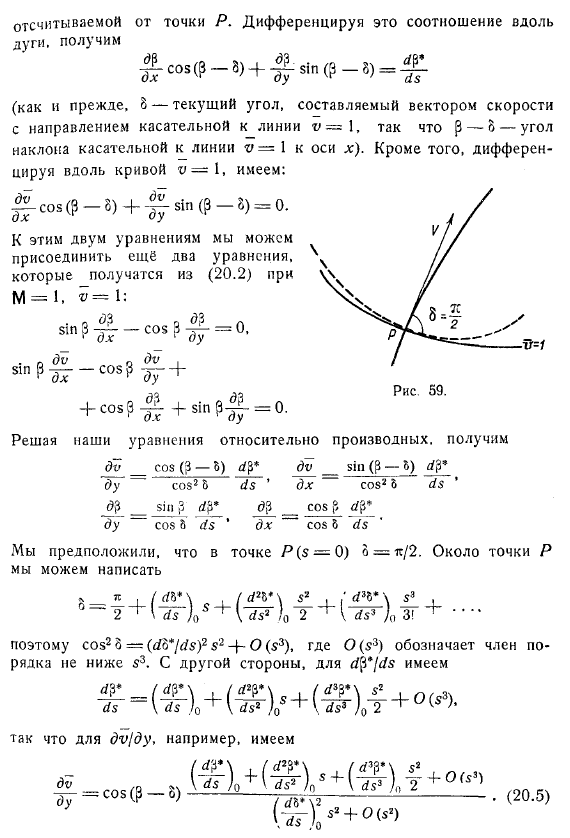
Может ли получиться бесконечное ускорение уже на самой линии v= 1 ? Согласно (20 .4) может представиться два случая. Если, то вектор скорости ортогонален в точке Р к переходной линии. Так как при вектор скорости должен быть ортогонален к характеристикам . Значит характеристики будут касаться в Р переходной линии (рис . 59) . Пусть Р = Р* (s) — значения угла на линии v=1 в функциях от длины дуги S, отсчитываемой от точки Р .
Дифференцируя это соотношение вдоль дуги, получим. Кроме того, дифференцируя вдоль кривой, имеем. К этим двум уравнениям мы можем присоединить ещё два уравнения, которые получатся из (20 .2). Решая наши уравнения относительно производных, получим .Мы предположили, что в точке. Около точки Р мы можем написать поэтому, где обозначает член по рядка не ниже .С другой стороны, для имеем.
Таким образом, для возможности непрерывного перехода от дозвуковой скорости к сверхзвуковой в том случае, когда в некоторой точке линия перехода ортогональна к вектору скорости (например, на оси симметрии сопла Лаваля), необходимо выполнение специальных условий относительно равномерности потока около этой точки. Людмила Фирмаль
- Если линия v = 1 сама является характеристикой (или во всех точках касается характеристик), то для непрерывности движения условие (20 .6) должно выполняться во всех точках этой линии, т . е .должно быть и линия перехода должна быть простой прямой .
В противном случае на всей линии перехода мы будем иметь бесконечные значения наших производных, т. е. бесконечные ускорения, и тогда движение нельзя продолжить за линию перехода (сама линия перехода будет предельной линией) и всё решение не будет иметь физического смысла. Простейшим примером такого решения может служить аналог источника или стока в несжимаемой жидкости.
Именно, если в цилиндрических координатах, то, так как по уравнению Бернулли, а вследствие уравнения неразрывности, мы можем написать: Если r — радиус того круга, на котором v обращается в единицу, то постоянная интегрирования будет . Мы можем, казалось бы, представить себе движение таким: на бесконечности v = 0, всюду vr < 0 — жидкость устремляется по радиусам к центру; скорость движения монотонно растёт по закону (20.7) и на окружности достигает критического значения.
Однако вдоль окружности будет так что (20.6) не выполняется. С другой же стороны, как нетрудно убедиться, написав уравнения характеристик в цилиндрических координатах, все характеристики должны касаться окружности. Движение наше не может быть продолжено внутрь круга радиуса самом деле, знаменатель (20 .7) имеет максимум, и следовательно, г имеет минимум в точности при v= 1.
Этот пример может служить иллюстрацией к сказанному в начале предыдущего параграфа о невозможности в сжимаемой жидкости осуществления таких течений, которые в жидкости несжимаемой давали бы бесконечные скорости. Вместо источника, или стока в начале координат, которые получаются в несжимаемой жидкости, мы имеем здесь ядро в виде круга радиуса, внутрь которого течение нельзя продолжить.
Вернёмся теперь к общему случаю, когда о (см. рис. 60). Нетрудно убедиться, что движение, возникающее в сверхзвуковой области сразу за линией перехода, будет принадлежать к типу смешанных течений по Хрнстиановичу. Действительно, найдём изменение 9 при перемещении по характеристике. Полная производная по х при перемещении по характеристике будет. Продифференцируем (20 .8) ещё раз по и определим эту производную на линии перехода.
Таким образом, если мере передвижения от какой-либо точки Р переходной линии по характеристике 1-го семейства ф будет расти, то при перемещении or Р по характеристике 2-го семейства ф будет убывать. Ясно, что это может быть лишь в случае смешанного течения (рис .об и 57). Итак, за переходной линией действительно может возникнуть предельная линия, в чём мы и имели случай убедиться на конкретных примерах § 19 .

