Определение несобственных интегралов

Определение несобственных интегралов

Определение несобственных интегралов. Неограниченная функция на отрезке не интегрируется по Риману на нем (теорема 1,§ 27.2).Если функция определена в бесконечном интервале, то определение интеграла применяется только к функции, определенной в интервале, поэтому его нельзя объяснить о его Интеграле Римана. В этом разделе обобщается понятие интеграла как для случая функции, определенной с неограниченным интервалом, так и для случая неограниченной функции, определенной с ограниченным интервалом. Определение 1.Функция [конечный или бесконечный полупериод[a, b), co a 6. = Определяется ^ + 00 и считается интегрируемым по Риману в любом интервале[a, r|], a> r / 6.

Это делается с переходом к пределу, в дополнение к пределу, на котором вводится интеграл Римана. Людмила Фирмаль

• Если он существует Mn (x) Yx, функция/называется интегрируемой в несоответствующем » В замкнутом смысле интервалов[a, b) указанный предел называется его неправильным интегралом、 Но… Итак (рис. 130)} (x) yx ^ Fri] {(x) yx. (33.1） Если предел (33-1) существует(и поэтому конечен)、 Также неправильный Интеграл Иначе она будет расходиться. В отличие от неправильных интегралов, обычный Интеграл Римана иногда называют его собственным интегралом. Наличие неправильного интеграла§ / (x) xx эквивалентно Наличие неправильного интеграла / / (x) х ce (a, b). фактически, Интеграл/(x) cx отличается от интеграла Святой Грааль^ {(x) dx (для e m]&) не зависит от [M]на конечном Граале、 Количество^ /(х) ух. Таким образом, для x\ * Интеграл$и 5 являются Или если нет предела и есть Из неверных интегральных определений(33.1) и (33.2).

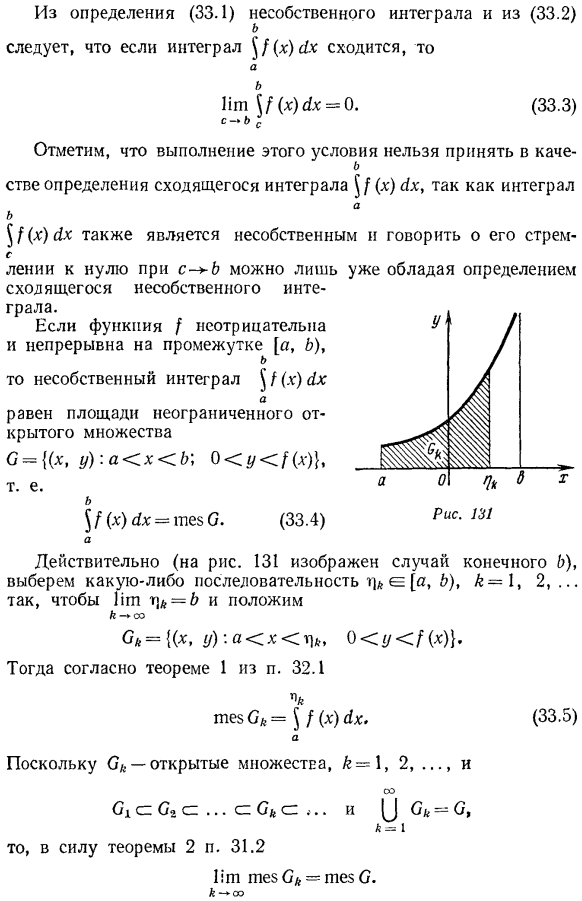
Если Интеграл^ {(x) xx сходится、 Заметим, что интеграл не может быть принят в качестве определения конвергентного интегрирования (x) χ. §/(х) ух неуместен、 если вы исчезаете до нуля как c + b, у вас может быть только неадекватное определение сходящихся интегралов. Если функция/неотрицательна и непрерывна на интервале[i, b)、 Тогда несобственный Интеграл$ /(х） Равняется площади неограниченного открытого множества Действительно (если конечный b показан на рисунке 131), выберите несколько последовательностей ck e [x, b).k= 1, 2, … Итак, тгr \ K = B и положим Тогда, согласно теореме§ 32.1 1 K 1, 2, потому что Ok-это открытый набор.

• Тогда по теореме 2. 31.2 Согласно определению неправильного интеграла Итак, когда мы достигнем предела эквивалентности k °°(33.5), мы получим (33.4). Неправильное интегральное определение (33.1） § / (х) DX [я, б） Только если функция[не ограничена какой-либо окрестностью точки x = b, то есть любым интервалом (b-e, b) (0 e& i). она может быть интегрируемой по Риману на любом интервале[i, m}], A ^ r] Cb + oo (для удобства отображения), и все функции, ограниченные полуинтервалом[i, b), являются Он интегрируется Риманом, и сечение[i, b]относительно расширения в точке x = b кроме того, Интеграл Римана функций, определенных таким образом, равен пределу (33.1) и поэтому не зависит от выбора дополнительных значений функции x = b. In этот смысл, Интеграл Римана является частным случаем неправильного integral.

So, остальные веса представления имеют смысл только в том случае, если функция определена с бесконечным интервалом или конечна, а в последнем случае они неограниченны(рис.132). Упражнение. 1.Функция (полуинтервал[a, разделенный b) является co a b + oe и делает Интеграл Римана возможным на любом интервале [a, d), и t] b. In в этом случае предел тm \ {(x) c1x всегда равен Если функция / существует и функция / определена произвольно для x = b, то этот предел равен интегралу Римана интервала / [a, b \от указанной функции. 2.

Значение здесь понимается в том смысле, что для ограниченного подынтегрального выражения, определенного в ограниченном интервале, теорема, доказанная ниже, тривиальна или доказана ранее. Людмила Фирмаль

• Пример неотрицательной функции a 非> 1, она неограничена в любой окрестности+с функцией+, и неправильный Интеграл сходится Если функция^определена в полуинтервале вида (a, b] 9 ao a b + co и Римана интегрируемы во всех сегментах kax [ ^ , b], то неправильный Интеграл Делается это по формуле Однако, если функция/определена в интервалах (a, b)、-°°= ^-（-°°、 и для выбора точек ce (a, b) Неверный Интеграл (/(x) хχ (значение (33.6)))) и ^ 1 (х) DX (значение (33.1)) по определению、 Кроме того, существование и значение интеграла Из выбора точек ce (a, b). фактически, в рассматриваемом случае функция / явно интегрируема по Риману в любом отрезке [ / Где правая сторона-предел функции 2 переменных.

Смотрите также:

Предмет математический анализ

Работа силы.	Формулы интегрального исчисления для несобственных интегралов.
Вычисление статических моментов и центра тяжести кривой.	Несобственные интегралы от неотрицательных функций.