Свойства меры открытых множеств

Свойства меры открытых множеств

Свойства меры открытых множеств. Теорема 1 (монотонность меры). 0 и гамма плоские открытые множества、 Доказательство. Как упоминалось выше, набор квадратов ранга м, расположенном вместе с границами набор O и T, соответственно, представлен компанией » 3М » (6) и 3М (Т).m= 1, 2,…И условия(31.5) являются Откуда Если множество 8m (0) и 5m (T) состоит из конечного числа квадратов, это связано с тем, что площадь заключающего многоугольника не меньше площади заключенного многоугольника, и что по крайней мере одно из множеств 3m (0) и (D) содержит бесконечно много квадратов-от 3m до 3m до 3M. Если мы перейдем το к пределу неравенства (31.7)、 (31.3) получаем неравенство (31.6). Ноль Теорема 2. O и Ok, k = 1, 2,…

В этом случае каждое множество является ограниченным замкнутым множеством, поэтому оно является компактным множеством. Людмила Фирмаль

• Давайте попробуем полностью открыться Множество, Ah = C2. •* СД СД Си… И 0 = y ок, то Если в некотором k0 mes Ok = + oo, то в соответствии с теоремой 1 для всех k> ko mes0k = + c «;в этом случае равенство (31.8) означает meso = + oo. Сначала докажите лемму. Лемма 1. Ck (k = 1, 2,…(Раскройте) плоский набор и после этого、 E-это компакт、 Тогда существует следующее число k0: Доказательство леммы. Из (31.10) и (31.11), система{Ok}, k-1, 2,…Образуют открытую крышку множества E. следовательно, согласно теореме об открытой крышке компактного множества (см. теорему 18.3 4), существует конечная крышка| C,…А набор е по К0, К… указывает максимальное количество kt. By условие (31.9), становится равным Т.

Доказательство теоремы 2.Во-первых, условие Ox c. C2 c … Ч. К. А… Следуя ей (см. теорему 1） Таким образом, последовательность 0k, k = 1,2,…всегда ограничена конечным или+ω. Рассмотрим 2 случая. 1.Весь набор 3m (0), m-0, 1,…Допустим, квадрат состоит из конечного числа squares. In Поэтому для леммы 1, для любого числа m, существует следующее число m: В этом случае выберите kt и установите для него значение kt kt. Это можно сделать в любое время, например: число k1.К2…. kt-1 выбирается в соответствии с Леммой 1 для множества zm(0), если множество Cn найдено следующим образом.

• Затем он показывает натуральных чисел, как КТ КТ КТ-1 и КТ ^ п \с КТ, то 0pa0ct, так что ТТ(0) С. 0ct. Таким образом, построенная последовательность km, m-1, 2,…является подпоследовательностью последовательности натуральных чисел. Здесь множество всех внутренних точек множества ct (0) обозначается ct (0).Очевидно, что 3m(0) является открытым множеством, а 3m(0) azt (0) aOct. Таким образом, по теореме 1 Окао позже, к-1, 2,…, По той же теореме 1 Он получается путем объединения неравенств (31.16) и (31.17). Если вы пройдете этот предел неравенства, м-+ ОО、 Последовательность{cc}является.

Конечные или бесконечные пределы, следовательно, совпадают с пре Поэтому проблема его подпоследовательности Г. е. Равенство (31.8). 2.Мы предполагаем, что существует агрегат 3m (0), содержащий бесконечно много квадратов. Потом ПЛ. 3m (0)= + co, следовательно, в этом случае、 предположим, что e 0 задано и ct © состоит из бесконечного множества квадратов. Площадь каждого квадрата ранга м Исправьте положительное целое число n на n / 102t e、 5 M (0) n квадратов на выбор. Обозначим через B множество их точек. Так как множество B является многоугольником (объединением конечного числа квадратов), то ограниченное замкнутое множество, то есть компактное, и далее Благодаря Лемме существует следующее число k.

Примером неограниченной плоской области с бесконечными измерениями является полоса. Людмила Фирмаль

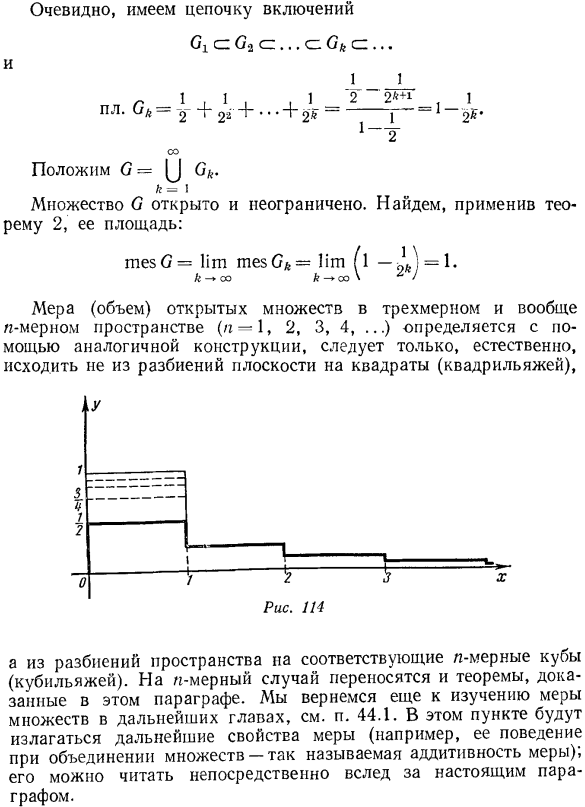
• Согласно теореме 1 и формулам (31.19) и (31.20), многоугольник B Из B показывает множество внутренних точек. (31.13) по всем k ’ ^ k Это означает достаточность условий (31.18). Тс Например, квадрат 1-го ранга включается бесконечно、 Чтобы построить пример неограниченной области с конечной площадью, выполните следующие действия: 2-единичный квадрат. Поставь В общем Каждый набор нормально работает(почему? это не. Формирование множества Ok можно представить следующим образом: Cx-квадратная половина 2; чтобы получить C2, возьмите другую половину квадрата 2 и примените ее правильно к O и получите O2.

In кроме того, половина оставшейся части квадрата 2 уже применяется к С3 (рис.114) и так далее. Очевидно, существует цепочка включений С = г 0К. Набор C открыт и неограничен. Применив теорему 2, можно увидеть ее площадь. 3-мерное и вообще n-мерное пространство (i= 1、2、3、4、…Измеренное значение (объем) открытого набора определяется с использованием аналогичной структуры. 、 А от раздела пространства к соответствующему-объединить кубики (как кубики).Доказанная теорема также переносится в случае размерностей.

Смотрите также:

Предмет математический анализ

Интегралы от вектор-функций.	Вычисление площадей.
Определение меры (площади) открытых множеств.	Объем тел вращения.