Оглавление:



Определение интеграла по Риману
Определение интеграла по Риману. Разбиение X интервала [a, b], точки x, -, r-0, 1, 2,…напомним, что k-произвольная конечная система (см.§ 16.5). Кроме того, записывается m = {x;}‘^.Каждый сегмент[ху. * «]、 1 = 1, 2,…, k называется сегментом раздела M, его длина Dx, Ax = x! X, 1 = 1, 2,…6 февраля. Значение Степень детализации разбиения называется m. Раздел x в сегментах[a, 6]называется После раздела m (или после раздела m) в том же сегменте, и если каждая точка в разделе m также является точкой в разделе m, она называется в разделе m. In другими словами, если каждый сегмент раздела m является частью сегмента раздела m (m ’также называется улучшенной версией раздела). В этом случае они пишут t’T или эквивалентный t-Zt’. Вся секция всех секций в данном сегменте имеет следующие свойства: 2°.Для любых х и Х2, х например, Х ^-ХХ и Х ^-Х2 существует.
Определение интеграла может быть сформулировано по-разному, так что определение предела функции может быть сформулировано двумя эквивалентными способами с помощью ограничения последовательности и с помощью языка эпсилон-дельта. Людмила Фирмаль
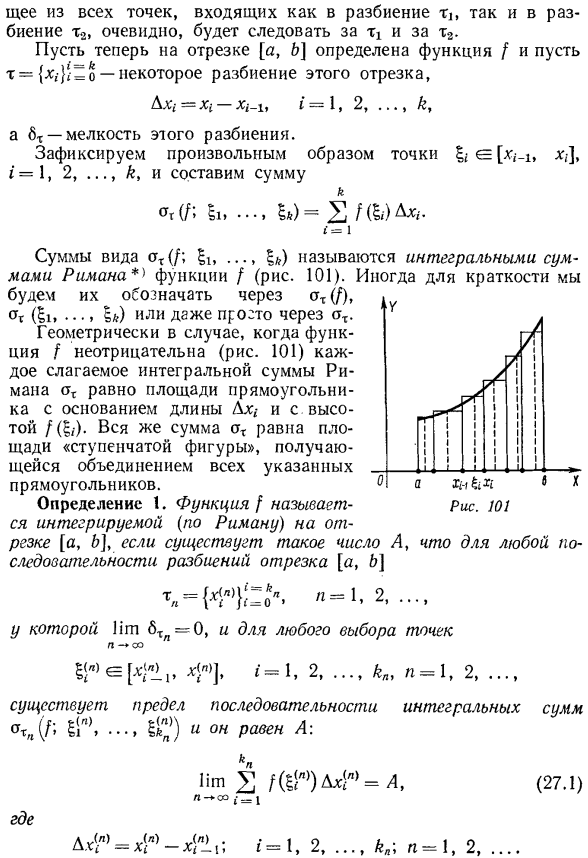
- Фактически, первое свойство выводится из того факта, что условие x3 e-x2 означает, что каждый сегмент раздела x3 включен в некоторый сегмент раздела m2, и что каждый сегмент раздела Xx включен в некоторый сегмент раздела Xx в соответствии с условием x2> Xx.; следовательно, все сегменты раздела x3 находятся в определенном сегменте раздела Xx. это x3b-xxЧтобы доказать 2-ю характеристику раздела, если указаны 2 раздела xx и x2, раздел m равен Из всех точек, содержащихся как в разделе x1}, так и в разделе m2, четко следует Tx и m2. Определить функцию/с интервалом[a, b], m = {x.} » =o-некоторое разбиение этого отрезка、 И-тонкость этой перегородки. Точка e [x; x, x в любом случае;]、1 = 1、2、…зафиксируем K и настроить сумме ( / ; у… сумма форм интегрального Римановой суммой функции/, Калифорния) называется Интеграл риманова сумма*(рис. 101).
Чтобы быть кратким, ЭЛТ (/), ЭЛТ(| х,…1k), или может быть просто представлен ЭЛТ. Если это работает геометрически! Неотрицательный (рис. 101), член Римановой интегральной суммы oX, основание и высота длины Ax/(?Площадь прямоугольника (.).Общая площадь ah будет равна площади «ступенчатой фигуры», полученной путем объединения всех этих прямоугольников. Определение 1.Функция/называется интегрируемой (по Риману) в интервале[a,&].Если число A присутствует для последовательности разбиения интервала[a, b] Она существует. Предел последовательности.| * , i)) и°n равно A Интегральная сумма Куда? Если золото 8Ty = 0, и если вы выбрали любую точку.
- При этих условиях число а называется (Риманом. По некоторому интегралу от/на интервале[a, b]、 ^ / (x) встречается в yx. Выражение§ / (x) yx читается как»интеграция из a в b /(x) yx». иксИнтервал[a, b] называется интервалом интегрирования. Подобный этому Где последовательность xn такова, что Hm 6 ^ = 0. Для простоты, в этом случае мы напишем: Определение 2.Число A называется определенным интегралом функции на отрезке[a, b], если для любого e 0 существует b = b (e) 0, а разбиение m = {;}.Каким бы ни был интервал[a, b] o, его тонкость меньше 6T 6, а точки$, e [x, x.], неравенство Упражнение 1.Докажите, что 2 Данные за пределами определения конкретного интеграла эквивалентны. Из определения I неотрицательная функция b Для 6x-0 определенный интеграл§ / (x)) x является пределом.
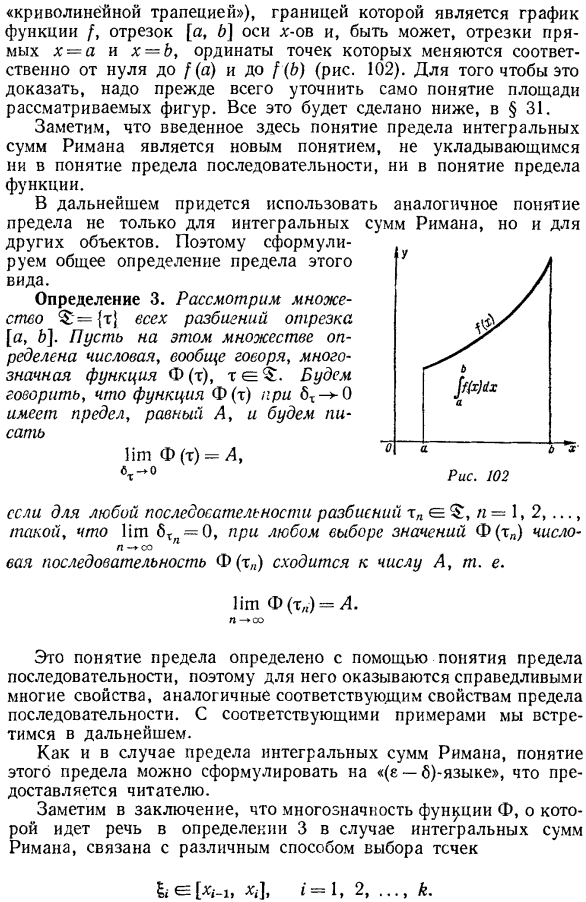
Ряд областей с соответствующими ступенчатыми формами. Таким образом, мы видим, что он естественным образом связан с понятием площади. То есть она будет равна площади фигуры «( * Термин «геометрия»хорошо известен в базовой геометрии и используется везде в смысле»плоского множества«. «Криволинейная трапеция»), ее границей является граф функции/, отрезок оси x[a, b]и, возможно, отрезок прямой x-a и x = b, а ордината этой точки находится от 0 до [(a) и 102 f (b) соответственно (рисунок).чтобы доказать это, мы должны сначала уточнить понятие области рассматриваемых чисел. Все это будет обсуждаться позже в§ 31.
Заметим, что введенное здесь понятие предела Римановой интегральной суммы является новым понятием, не укладывающимся ни в понятие предела последовательности, ни в понятие предела функции. Людмила Фирмаль
- В дальнейшем необходимо использовать понятие аналогичного ограничения не только для интеграла Римана, но и для других объектов. Поэтому мы формулируем общее определение этого вида ограничения. Определение 3.Все разбиения в множестве φ= {m / интервал[a, b]. в этом множестве мы предполагаем, что числовая многозначная функция Φ (τ) определена в общих терминах. Он говорит, что функция Φ (τ) в 8X-0 имеет предел, равный A.
Смотрите также:

