Оглавление:
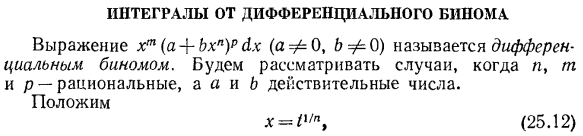



Интегралы от дифференциального бинома
Интегралы от дифференциального бинома. Формула xm (a + bxn) P xx (af 0, bΦ0) называется дифференциальным биномом. рассмотрим случаи, когда n, m и p-рациональные числа, а a и b-вещественные числа. Поставь Следовательно, Интеграл Подстановка (25.12) уменьшает тип до целого числа Где P и Q-рациональные. Если на стадии рассмотрения Первый случай. п-целое число. 7=^, где r и 5-целые числа. По результатам.
На этот раз подстановка приводит к интегралу рационального числа. Людмила Фирмаль
- В терминах 25.2 в этом случае подстановка r = / / $сводит Интеграл(25.14) к интегралу рациональной дроби. 2-й случай. d-целое число. Теперь пусть p = r / 5, r и 5-целые числа. Согласно результатам пункта 25.2, в этом случае дается Интеграл (25.14). Присваивая R =(a + b)$Интегралу рациональной дроби. 3-й случай. Р + 7-это целое. пусть p = R / a и 5-целые числа. Для наглядности опишите Интеграл (25.14) в несколько иной форме. Опять же, существует Интеграл того типа, который мы рассматривали в том же разделе 25.2. Итак, в 3 случаях.
- Если либо число p, q, либо число p + 7 является целым числом, то Интеграл (25.14) с указанными выше подстановками будет Интегралом рационального числа. Применительно к интегралу (25.13) этот результат равен Следующим образом. Если любое из чисел p, 1 или—+ P является целым числом, то Интеграл (25.13) является интегралом От рационального человека number. In кроме того, если p-целое число, это сокращение выполняет подстановку.
П. Л. Чебышев показал, что интеграл (25.13) не выражается в элементарных функциях для показателей m, n и p, которые не удовлетворяют приведенным выше условиям. Людмила Фирмаль
- Где число 5 является знаменателем дроби, т. е.=〜;. если when-целое число, если является-знаменатель дроби P, т. е. P = R. Если > / P-целое число, то заменить Где число 5 также является знаменателем дроби р. Пиар и меры. Рассмотрим Интеграл Где m-2, n =-2, p = ^ u-1; 2-й случай. Отсюда Сделайте вышеуказанную замену. И так оно и есть.、 Где r представлен x в соответствии с формулой (25.15). * ’П. Л. Чебышев (1821-1894) русский математик.
Смотрите также:

