Обучение младших школьников решению логических задач - Понятие "логическое мышление" и условия его развития у младших школьников в процессе обучения математике

Оглавление:

Мыслительные процессы всегда были одним из самых сложных предметов для изучения. На протяжении тысячелетий человек изучал окружающий его мир во всем его многообразии, пытаясь заполнить пробелы в своих знаниях, используя опыт предыдущих поколений. Современная наука прошла долгий путь в изучении мира, но изучение самого человека до сих пор представляет собой нерешенную проблему.

Чтобы познать мир, недостаточно просто заметить связь между явлениями, необходимо установить, что эта связь является общим свойством вещей. На этой обобщенной основе человек решает конкретные когнитивные задачи. Логическое мышление дает ответ на такие вопросы, которые не могут быть решены путем непосредственного, чувственного размышления.

В соответствии с вышесказанным, проблема данной работы заключается в исследовании наиболее продуктивных способов развития логического мышления учащихся средних классов на уроках математики. Благодаря развитию навыков индивидуального мышления дети способны правильно ориентироваться в окружающем мире, применяя ранее полученные обобщения в новой, конкретной обстановке.

Развивая логическое мышление, мы способствуем работе интеллекта, а интеллект — это гарантия личной свободы человека и независимости его судьбы. Чем больше ребенок использует свой интеллект для анализа и оценки происходящего, тем менее он восприимчив ко всем попыткам манипуляций извне.

Как показывает практика, систематически решая логические задачи, головоломки, ребусы и т.д., неоднократно меняя и усложняя упражнения, ум ребенка оттачивается, он становится более находчивым и сообразительным. Меняется их подход к решению проблем. Рассуждения студента становятся последовательными, доказательными и логичными, а язык — ясным, убедительным и продуманным.

Трудно переоценить роль развития навыков рассуждения у детей младшего школьного возраста. Он повышает интерес к предмету, формирует нестандартное мышление, умение анализировать, сравнивать, обобщать и применять знания в нестандартных ситуациях.

С переходом на новые государственные образовательные стандарты современные школы нацелены на личностное и когнитивное развитие учащихся, чтобы научить их умению учиться. Особенно это касается преподавания математики. Проблема развития мышления звучит очень актуально. Стандарт второго поколения в математическом образовании учащихся начальной школы не означает революцию. Она поддерживает традиции начального математического образования, но расставляет иные акценты и определяет иные приоритеты. Определяющим фактором постановки целей, отбора и структурирования содержания, условий его реализации является значимость математического образования в начальной школе для дальнейшего образования в целом и математики в частности, а также возможность применения знаний и умений при решении любых практических и познавательных задач. В стандарте указано, что в процессе освоения предмета студент должен уметь овладеть «основами логического и алгоритмического мышления, получения и выполнения алгоритмов».

Обучение младших школьников решению логических задач

Понятие «логическое мышление» и условия его развития у младших школьников в процессе обучения математике

O.K. Тихомиров в своей «Психологии мышления» определяет логическое мышление как «рассуждение и теоретическое мышление», которое «характеризуется использованием понятий, логических структур, существующих на основе языка, языковых средств». Он также называет это аналитическим мышлением, которое растянуто во времени, имеет четко определенные этапы и в значительной степени представлено в голове самого мыслителя.

Проблему развития мышления учащихся изучали многие зарубежные и отечественные ученые. Я. Гальперин, В.В.Давыдов, Д.Дьюи, А.Н.Леонтьев, В.К.Ягодовская, А.С.Пчелко, Н.С.Рождественский, И.Л.Никольская, Ж.Пиаже, С.А.Рубинштейн , А.А.Столяр , Д.Б.Эльконин , Ю.И.Шрейнер, Л.С.Выготский, И.Я.Яковлев. Лернер, Д. Н. Середа, М. Н. Скаткин и другие.

Они теоретически и экспериментально доказали, что нынешняя школа еще не обеспечивает своим выпускникам необходимый уровень развития мыслительной деятельности. По их мнению, для успешного изучения и понимания учебного материала студенты должны обладать тремя компонентами мышления:

1) высокий уровень элементарных мыслительных операций: Анализ, синтез, сравнение, обобщение, выделение существенного, классификация и т.д;

2) высокий уровень активности, раскованности мышления, проявляющийся в продуцировании большого количества различных гипотез, идей, появлении множества вариантов решения проблемы;

3) высокий уровень организации, проявляющийся в ориентации на существенное в явлениях, использовании обобщенных схем анализа явления.

Никто не будет отрицать, что любой учитель должен развивать логическое мышление учеников. Об этом говорится в методической литературе, в пояснениях к учебным программам. Практика преподавания показывает, что развитие мышления учащихся практически ставится как цель обучения по каждому предмету. Считалось, что при обучении математике логическое мышление развивается автоматически, без целенаправленной работы. Особое внимание роли математики в развитии логического мышления уделяли некоторые исследователи, например, Никольская И.Л.. , Ивин А.А. и др.

Опыт показывает, что целенаправленное, систематическое формирование логических понятий и действий может происходить на уроках математики, так как в силу своей специфики она содержит большой потенциал для развития логического мышления учащихся младших классов.

В настоящее время известно несколько специальных программ, направленных на развитие логического мышления. К сожалению, они не всегда реализуются на практике. В результате работа по развитию логического мышления учащихся проводится «в общем», без знания системы необходимых приемов, без знания их содержания и порядка формирования. Это приводит к тому, что развитие логического мышления происходит во многом стихийно, поэтому большинство учащихся не овладевают первыми приемами мышления. В результате не происходит полноценного развития ученика младших классов и формирования у него логических универсальных действий, что полностью противоречит требованиям нового образовательного стандарта.

Следует обратить особое внимание на такие мыслительные процессы, как индукция и дедукция. Индукция и дедукция — это способы получения выводов, которые отражают направление мышления от частного к общему или наоборот. Индукция подразумевает выведение общих суждений из частных, а дедукция — выведение частного суждения из общего.

Возрастные особенности развития логического мышления в младшем школьном возрасте

Мышление детей младшего школьного возраста значительно отличается от мышления детей дошкольного возраста. Для мышления дошкольников характерны такие особенности, как непроизвольность мышления, низкая контролируемость при постановке мыслительной задачи и при ее решении, они чаще и легче думают о том, что их интересует. Младшие школьники, когда речь идет о регулярном выполнении обязательных заданий, учатся контролировать свое мышление, думать, когда это необходимо, а не только когда это интересно, когда им нравится то, о чем они должны думать.

Конечно, в 6-7 лет понятийное мышление еще не сформировано, но зачатки такого мышления уже есть.

Л.С. Выготский начал изучать детское мышление и его развитие, особенно переход от практического к логическому мышлению. Он также обозначил основные пути и условия этого перехода. Эти исследования, продолженные А.А. Люблинской, Г.И. Минской, Г.А. Ганьковой, показали, что практическое действие остается «в резерве» даже на самом высоком этапе развития логического мышления у детей младшего школьного возраста. «Мышление руками» остается «резервом» даже у подростков и взрослых, когда они не могут сразу решить новую задачу вербально — в голове.

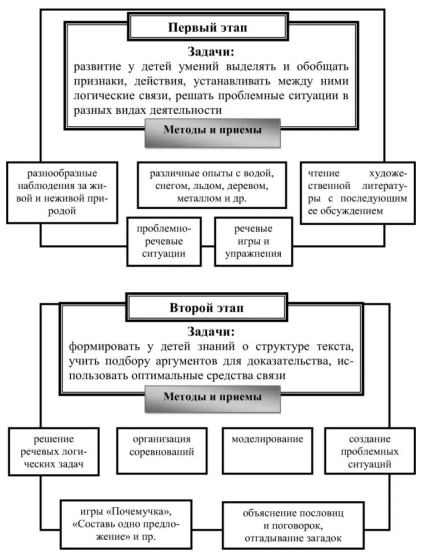
Концепция «постепенного мышления», разработанная P.Y. Гальперин основывается на понимании роли практической деятельности как начального этапа в развитии всех высших форм человеческого мышления. На первом этапе ребенок использует внешние материальные действия для решения проблемы. На втором этапе эти действия только представляются и вербализуются ребенком (сначала вслух, затем наедине). Только на последнем, третьем этапе внешнее предметное действие упрощается и переходит на внутренний уровень.

Когда мышление ребенка переходит на следующую, более высокую ступень развития, его первоначальные формы, особенно практическое мышление, не исчезают, но их функции в процессе мышления перестраиваются и изменяются. Например, высшее, вербальное мышление играет решающую роль в работе многих специалистов, чья работа связана с визуализацией и творчеством — архитекторов, художников и т.д. Однако такой специалист постоянно зависит от конкретных образов и практических действий.

По мнению А.А. Люблинской, логическое мышление обнаруживается прежде всего в ходе самого процесса мышления. В отличие от практического мышления, логическое мышление осуществляется только вербально. Человек должен рассуждать, анализировать и мысленно устанавливать необходимые связи, чтобы выбрать и применить соответствующие правила, приемы, действия для решения конкретной задачи, которая ему известна. Он должен сравнивать и устанавливать связи, которые он ищет, группировать то, что отличается, и различать то, что похоже, и все это делается только с помощью умственных действий. У детей младшего школьного возраста мы постоянно внимательно наблюдаем за вербальным способом проявления логического мышления: при решении задач на уроках математики, написании слов на уроках чтения и письма и так далее.

Операция сравнения имеет большое значение в учебной деятельности старшеклассника. В конце концов, большая часть обучения в младших классах основана на сравнении. Эта операция является основой для классификации явлений и их систематизации. Чтобы овладеть операцией сравнения, человек должен научиться видеть подобное в другом и другое в подобном. Исследования А.И. Кагальняка, А.Л. Савченко, Е.Н. Шиловой, Т.В. Космы и многих других убедительно показали, что ошибки в операции сравнения являются результатом неумения учащихся вырабатывать подходящее умственное действие для решения определенной задачи.

Понятие логической задачи в начальной школе

Признание выдающейся роли предмета математики в развитии логического мышления школьников неоспоримо. Причина такой исключительности в том, что это самая теоретическая из всех наук, изучаемых в школе.

Выдающийся русский математик А.Н. Колмогоров писал: «Математика — это не просто язык. Математика — это язык плюс рассуждения, это как язык и логика вместе. Математика — это инструмент для логических рассуждений. Она объединяет результаты точного мышления многих людей. В математике одно рассуждение может быть связано с другим. Кажущаяся сложность природы с ее странными законами и правилами, каждое из которых имеет свое очень подробное объяснение, на самом деле тесно связаны между собой. Однако, если вы не готовы использовать математику, вы не увидите, что логика позволяет вам переходить от одного к другому в этом огромном разнообразии фактов».

По сей день не существует единого определения термина «задачи». В Большой советской энциклопедии под задачей понимается один из методов обучения для проверки знаний и практических навыков учащихся, используемый в начальной, средней и старшей школе. Задача является средством развития логически правильного мышления учащихся и обязательно содержит четко выраженное или подразумеваемое условие и главный вопрос, решение которого является ответом.»

Одна из основных задач логики — определить, как от посылки перейти к заключению (правильное рассуждение) и получить истинное знание об объекте рассмотрения, чтобы глубже понять нюансы исследуемого объекта мышления и его связи с другими аспектами рассматриваемого явления.

Задача — это проблемная ситуация с явно выраженной целью, которую необходимо достичь; в более узком смысле задачей также называют саму цель, заданную в рамках проблемной ситуации, то есть то, что необходимо сделать. В первом значении задача может быть, например, ситуацией, в которой необходимо достичь очень высокого объекта; второе значение слышится в высказывании: «Ваша задача — достичь этого объекта». Несколько более жесткое понимание «задачи» предполагает, что не только цель, но и условия задачи, которая в данном случае определяется как преднамеренная проблемная ситуация с выделенными условиями (данными) и требованием (целью), являются явными и определенными.

В педагогической практике термин «задача» приобретает более узкое значение и обозначает упражнение, в котором целью является нахождение решения по известным данным с помощью определенных действий (рассуждения, вычисления, перемещения элементов и т.д.), соблюдая определенные правила выполнения этих действий (логическая задача, математическая задача, шахматная задача).

В начальном обучении математике под задачей понимается специальный текст, в котором изложена определенная житейская ситуация, характеризующаяся числовыми компонентами, между которыми обязательно существует определенная зависимость. Таким образом, текст задания можно рассматривать как вербальную модель реальной действительности.

Актуальность задачи интеллектуального развития личности, важнейшим компонентом которого является формирование логических способностей, обусловлена рядом причин. Качество обучения во многом зависит от уровня развития мышления учащихся: логически развитое мышление позволяет легче и шире усваивать различные знания.

В психолого-педагогических исследованиях и практике логического обучения детей младшего школьного возраста экспериментально доказано, что «младший школьный возраст чувствителен к усвоению обобщенных способов и средств умственной деятельности; содержанием логического обучения является формирование логических способностей в процессе обучения школьным предметам на всех его этапах…».

Логическая задача (Логическая задача)

Логическая задача (логическая задача) — это задача, решение которой обычно требует логического мышления, смекалки, иногда использования нестандартного мышления, а не специальных знаний на высоком уровне.

Логические задачи, как и математические, называют «гимнастикой ума». Но в отличие от математики, логические задачи — это веселая гимнастика, которая в увлекательной форме позволяет вам проверить и потренировать свои мыслительные процессы, иногда неожиданным образом. Для их решения требуется воображение, иногда интуиция, но не специальные знания. Решение задач по логике заключается в тщательном анализе условия задачи, распутывании клубка противоречивых связей между символами или объектами. Логические задачи для детей — это, как правило, целые истории с популярными актерами, к которым нужно просто привыкнуть, чтобы прочувствовать ситуацию, визуализировать ее и уловить связи.

Даже самые сложные логические задачи не содержат чисел, векторов, функций. Но именно здесь на помощь приходит математическое мышление: оно заключается в том, чтобы понять и осознать условия логической задачи. Самое очевидное, поверхностное решение не всегда является правильным. Но чаще всего, несмотря на запутанное состояние, решение логической головоломки оказывается гораздо проще, чем кажется на первый взгляд.

Разнообразие логических задач очень велико. Более того, в базовом курсе математики более удачной классификацией логических задач является классификация, предложенная Е.Ю. Выделяют классификацию логических задач по ходу действий, выполняемых в процессе решения, а для базового курса математики комбинаторные задачи также являются логическими, так как учащимся не даются общие правила и нормы решения этих задач:

Задачи на установление соответствий между элементами различных множеств;
Комбинаторные задачи;
контроллеры для установления соответствий между элементами множеств; * комбинаторные задачи; * задачи на упорядочивание элементов множеств.
для установления временных, пространственных и функциональных отношений; * для активного опробования вариантов.
активное перечисление отношений вариантов.

В педагогической и методической литературе также используются подобные классификации логических задач:

в соответствии с содержанием умственной операции, участвующей в процессе решения (это: Аналогия; сравнение; дедукция, классификация; анализ и синтез; абстракция; обобщение);
в зависимости от характера требований (поиск искомого объекта, конструирование или преобразование, поиск процесса).
методами процесса решения (с использованием обоснований, таблиц, диаграмм, блок-схем и т.д.).

Решение логических задач тренирует логику, память и мышление.

Логические задачи и задачи на логику рассчитаны на разные возрастные контингенты и подходят для решения: дошкольникам, младшим школьникам, старшим школьникам и взрослым.

Способность выполнять логические действия не является врожденной. По мнению многих авторов, мыслительная деятельность успешно активизируется и развивается, когда «учащиеся осознают новые вопросы, задаются целью найти на них ответы, сначала в сотрудничестве с учителем, а затем самостоятельно, постепенно переходя от простых вопросов к все более сложным».

Элементарная логическая задача — это задача, характеризующаяся наличием логической связи между составляющими ее элементами. Благодаря этому она может быть решена срочно, при первом же предъявлении, на основе мысленного анализа ее условий [Крушинский Л.В.].

На странице курсовые работы по педагогике вы найдете много готовых тем для курсовых по предмету «Педагогика».

Здесь темы рефератов по педагогике

Читайте дополнительные лекции: