Построение корреляционных плеяд - Корреляция и взаимосвязь величин

Оглавление:

Корреляционные диаграммы используются для визуального представления результатов корреляционного анализа. Это не самостоятельный статистический метод, а лишь способ графического представления корреляционных связей.

Прежде чем строить корреляционные плеяды, необходимо понять, что такое корреляция и каковы особенности использования корреляционного анализа в психологических исследованиях.

Использование метода корреляционных плеяд в рефератах по психологии делает работу более презентабельной и показывает более высокий уровень осведомленности студента-психолога.

Существует два основных способа построения корреляционных заявлений:

Рисование с помощью инструментов Word.
Конструирование с помощью специальных программ.

Если вам необходимо построить корреляционную плеяду в дипломной работе по психологии, курсовой работе или магистерской диссертации, вы должны следовать следующему алгоритму:

Если имеется всего несколько психологических параметров и корреляций между ними, лучше построить корреляционное дерево с помощью редактора Word.

Если психологических параметров и корреляций между ними достаточно много, лучше использовать программы построения графиков, например, Graphviz.

Корреляция и взаимосвязь величин

Корреляция (от лат. correlatio «связь»), или корреляционная зависимость — статистическая связь между двумя или более случайными переменными (или переменными, которые можно считать таковыми с некоторой степенью точности). В этом случае изменения значений одной или нескольких из этих переменных сопровождаются систематическим изменением значений другой или других переменных.

Математической мерой корреляции двух случайных величин является корреляционное отношение или коэффициент корреляции. Когда изменение одной случайной величины приводит не к закономерному изменению другой случайной величины, а к изменению какой-то другой статистической характеристики данной случайной величины, такая связь не считается корреляцией, хотя и является статистической.

Термин корреляция был впервые введен французским палеонтологом Жоржем Кювье в XVIII веке. Он разработал «закон корреляции» частей и органов живых существ, который можно использовать для реконструкции внешнего вида ископаемого животного, имея лишь часть его останков. В статистике слово «корреляция» было впервые использовано английским биологом и статистиком Фрэнсисом Гальтоном в конце XIX века.

Значительная корреляция между двумя случайными величинами всегда свидетельствует о существовании некоторой статистической связи в данной выборке, но эта связь не обязательно должна наблюдаться в другой выборке и быть причинно-следственной по своей природе. Часто заманчивая простота корреляционных исследований приводит исследователя к ложным интуитивным выводам о существовании причинно-следственной связи между парами переменных, тогда как коэффициенты корреляции устанавливают только статистические связи. Например, изучая пожары в определенном городе, можно обнаружить очень высокую корреляцию между ущербом, причиненным пожаром, и количеством пожарных, участвующих в тушении пожара, причем корреляция будет положительной. Однако из этого не следует, что «большее количество пожарных приводит к большему ущербу», равно как и не будет успешной попытка минимизировать ущерб от пожара путем ликвидации пожарных бригад. Корреляция двух величин может указывать на наличие общей причины, даже если сами явления не взаимодействуют напрямую. Например, обледенение приводит как к увеличению травм при падениях, так и к увеличению количества автомобильных аварий. В данном случае две переменные (травмы от падений пешеходов и дорожно-транспортных происшествий) коррелируют, хотя они не связаны причинно-следственно, а имеют только одну общую третью причину — обледенение.

В то же время отсутствие корреляции между двумя переменными не означает, что между ними нет связи. Например, зависимость может иметь сложный нелинейный характер, который корреляция не выявляет.

Некоторые виды коэффициентов корреляции могут быть положительными или отрицательными. В первом случае предполагается, что мы можем определить только наличие или отсутствие взаимосвязи, а во втором случае мы можем определить и ее направление. Если предположить, что между значениями переменных существует связь строгого порядка, то отрицательная корреляция — это та, при которой увеличение одной переменной связано с уменьшением другой. В этом случае коэффициент корреляции будет отрицательным. Положительная корреляция в данном случае — это связь, при которой увеличение одной переменной связано с увеличением другой переменной. Возможна также ситуация, когда статистическая связь отсутствует — например, с независимыми случайными величинами.

Корреляционный анализ

Корреляционный анализ — это метод статистической обработки данных, который измеряет степень взаимосвязи между двумя или более переменными. Корреляционный анализ тесно связан с регрессионным анализом (также часто используется термин «корреляционно-регрессионный анализ», который является более общим статистическим понятием); он используется для определения необходимости включения определенных факторов в уравнение множественной регрессии, а также для оценки полученного уравнения регрессии на предмет соблюдения выявленных взаимосвязей (с помощью коэффициента детерминации).

Ограничения корреляционного анализа:
Его можно использовать, когда имеется достаточное количество наблюдений, подлежащих изучению. На практике считается, что число наблюдений должно быть как минимум в 5-6 раз больше числа факторов (существует также рекомендация использовать пропорцию, которая не менее чем в 10 раз превышает число факторов). Когда число наблюдений превышает число факторов в десять раз, вступает в силу закон больших чисел, который обеспечивает взаимное затухание случайных флуктуаций.

Необходимо, чтобы совокупность значений всех характеристик факторов и исходов подчинялась многомерному нормальному распределению. Если объем совокупности недостаточен для формального теста на нормальное распределение, закон распределения определяется визуально с помощью корреляционного графика. Если существует линейная тенденция в расположении точек в этом поле, то можно предположить, что все исходные данные подчиняются закону нормального распределения.

Начальный набор значений должен быть качественно однородным.
Корреляция как таковая не означает, что переменная предшествует или вызывает изменение, или что переменные причинно связаны друг с другом, а не с третьим фактором.

Область применения
Этот метод статистической обработки данных очень популярен в экономике, астрофизике и общественных науках (особенно психологии и социологии), хотя сфера применения коэффициентов корреляции очень широка: контроль качества промышленной продукции, металлургия, агрохимия, гидробиология, биометрия и так далее. В различных прикладных отраслях приняты разные границы интервалов для оценки тесноты и значимости связи.

Популярность метода объясняется двумя причинами: Коэффициенты корреляции относительно легко вычисляются, и их применение не требует специальной математической подготовки. Простота применения коэффициента в сочетании с легкостью его интерпретации привели к его широкому использованию в области анализа статистических данных.

Корреляционный анализ для двух случайных переменных состоит из:

Построение корреляционного поля и составление корреляционной таблицы;
Вычисление коэффициентов корреляции выборок и корреляционных связей.
Проверка статистической гипотезы о значимости ассоциации.

Основной целью корреляционного анализа является выявление взаимосвязи между двумя или более исследуемыми переменными, которая рассматривается как общая, связанная вариация двух исследуемых характеристик. Эта изменчивость имеет три основные характеристики: Форма, направление и сила.

Корреляционная плеяда

Метод корреляционных плеяд предназначен для нахождения таких групп параметров или объектов — «плеяд» — если корреляционная связь, т.е. сумма модулей коэффициентов корреляции между параметрами одной группы (внутриплеядная связь) достаточно велика, а связь между параметрами из различных групп (межплеменных) невелико.
Согласно определенному правилу на матрице корреляции, объекты образуют граф рисунка, который затем подразделяется на подграфы с помощью различных техник. Элементы, соответствующие каждому из подграфов, образуют плеяду.

Таким образом, корреляционная плеяда — это фигура, состоящая из вершин и соединяющих их линий. Вершины соответствуют параметрам и обычно обозначаются цифрами — номерами параметров. Линии соответствуют статистически значимым ассоциациям и графически показывают знак, а иногда и уровень
уровень значимости взаимосвязи. Корреляционный набор может содержать все статистически значимые отношения корреляционной матрицы (иногда называемой корреляционным графом) или только их значимая часть (например, соответствующая фактору по результатам факторного анализа).

Правила построения корреляционных сеток: Когда число наблюдений превышает число факторов в десять раз, вступает в силу закон больших чисел, который обеспечивает взаимное ослабление случайных флуктуаций.

Необходимо, чтобы совокупность значений всех характеристик факторов и исходов подчинялась многомерному нормальному распределению. Если популяция недостаточна для формального теста на нормальное распределение, закон распределения определяется визуально с помощью корреляционной диаграммы. Если существует линейная тенденция в расположении точек на этом графике, то можно предположить, что все исходные данные подчиняются закону нормального распределения.

Существует несколько правил построения корреляции
плеяды.

поскольку в корреляционных исследованиях присутствие
корреляции показывает только взаимосвязь изучаемых параметров, но не причинно-следственную зависимость,
то не рекомендуется использовать односторонние стрелки, указывающие направление корреляции, при построении корреляционных плеяд. Либо используются двусторонние стрелки, или простые соединительные линии.
прямые и обратные зависимости обозначаются (маркируются) различными графическими свойствами линий:
Например, прямые линии обозначаются сплошной линией, обратные линии — пунктирной.
корреляционный анализ может включать достаточно большое количество параметров, между которыми может возникнуть большое количество взаимосвязей, между которыми может возникнуть большое количество отношений. Для того чтобы фигура, отражающая эти отношения была читаема, важно расположение элементов корреляционного дерева относительно друг друга.

Как правило, параметр с наибольшим количеством значимых связей помещается в центр корреляционного дерева, а параметры со спорадическими связями — на периферию. Иногда исследователю важно сосредоточиться на корреляции только одного параметра. Затем он помещается в центр фигуры, а связанные с ним параметры располагаются вокруг него (игнорируя существующие связи между другими параметрами). Во многих случаях (и особенно в сравнительных исследованиях) факты дают информацию не только о наличии ассоциаций, но и об их отсутствии. Картина становится наиболее ясной, когда изображаются все измерения, участвующие в исследовании, даже если между многими из них может не быть никаких связей.

Построение плеяд с помощью Word и специальных программ

Построение корреляционной плеяды с помощью инструментов Word.
Во-первых, необходимо рассчитать корреляции между психологическими параметрами.

Далее на черновом наброске следует нарисовать расположение параметров и взаимосвязи между ними.

Следующий шаг — начать рисовать:

В Word мы выбираем «Вставка», «Фигуры», а затем используем прямоугольники, овалы, круги по своему усмотрению.
Вставьте названия психологических показателей в нарисованные фигуры.
Выберите «Вставка», «Фигуры», «Линии» и перетащите между линиями, которые отражают характеристики корреляции (ее знак и уровень значимости).
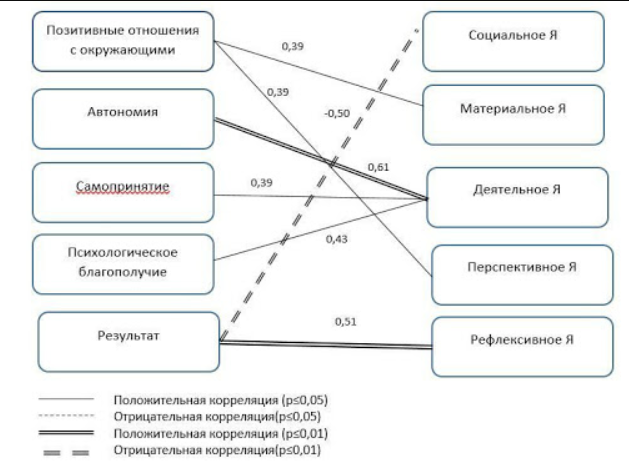
В качестве примера рассмотрим построение корреляционной родословной в исследовании корреляций между различными типами личностной идентичности с психологическим благополучием и смысложизненными ориентациями.

Рассчитываем коэффициенты ранговой корреляции Спирмена между показателями идентичности (измеряемой по методике Куна «Кто я») и показателями теста СЖО Д.А. Леонтьева и опросника «Шкала психологического благополучия» К. Риффа. Результаты значимых корреляций занесены в таблицу.
Поскольку в данном случае мы имеем два разных типа психологических показателей (с одной стороны, показатели идентичности, с другой — смысло-жизненные ориентации и показатели благополучия), логично противопоставить цифры с разными психологическими данными (см. рисунок).

Существуют следующие правила представления корреляций между психологическими параметрами на корреляционных плеядах в психологии ECD:

положительные корреляции — сплошная линия;
отрицательные корреляции — пунктирная линия;
Корреляции на уровне значимости 0,05 — простая линия;
корреляции на уровне значимости 0,01 — двойная линия.
Числовые значения корреляций должны быть написаны над линиями, соединяющими рисунки с обозначениями психологических показателей и отражающими связи между ними.

В приведенном выше примере психологических показателей и связей между ними не так много, а на рисунке с корреляционными плеядами четко видны корреляции. В ситуации, когда количество психологических показателей и корреляций между ними намного больше, становится трудно отображать их вручную. В этом случае для реализации метода корреляционных плеяд можно использовать специальные программы.

Построение корреляционного дерева с помощью специальных программ:

Существует несколько программ для построения корреляционных плеяд. Здесь корреляционные плеяды в строгой научной терминологии называются графами.

Графы — это набор некоторых объектов, связанных отношениями. В области психологии корреляционные связи между психологическими показателями представляются графически.

Суть программ построения графов заключается в том, чтобы в определенном редакторе в определенном формате задать психологические показатели и отношения между ними, а программа сама нарисует дерево корреляции в наиболее опт

На странице курсовые работы по психологии вы найдете много готовых тем для курсовых по предмету «Психология».

Здесь темы рефератов по психологии

Читайте дополнительные лекции: