Геометрический смысл частных производных и полного дифференциала

Геометрический смысл частных производных и полного дифференциала

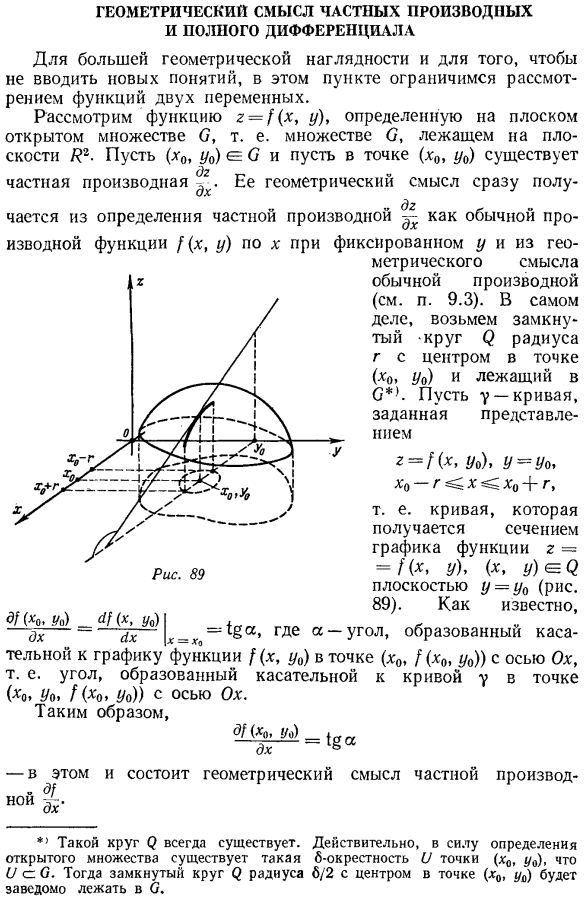
Геометрический смысл частных производных и полного дифференциала. Чтобы повысить геометрическую ясность и не вводить новые понятия, этот раздел ограничивается рассмотрением функций 2 переменных. Предположим, что функция r = f (x, y) определяется плоским открытым множеством O, то есть множеством O, расположенным на плоскости K2. (x0, y0) E 0 и заставить его существовать в точке (x0, y0) Частных производных. Его геометрический смысл сразу же становится полу Начинается с определения частной производной^как нормальной производной функции[(x, y) относительно X в фиксированном y и геометрического значения нормальной производной (см.§ 9.3).

тангенса угла наклона, образованного Касательная точек к кривой, полученной сечением графика функции Людмила Фирмаль

• Действительно, возьмем точку (x0, y0) в качестве центра и замкнутую окружность φ радиуса r, которая находится в точке 0 * K. То есть, кривой, полученной в раздел Графика функции Р = F (Х, У), (х, г)=плоскости у = У0 (рис. 89).Как вы знаете. касательная ((x, y0)) графика функции с осью l Ox (x0, f (x0, y0)), то есть угол, образованный касательной кривой y точки (*о） Подобный этому Это геометрия Значение частного производства * Такой круг 2 всегда есть present. In факт, по определению открытого множества, существует 6 соседей V точек (x0, y0), поэтому c. O. тогда замкнутый круг с радиусом 6/2, центрированный на точке (x0, yy), 01, явно находится в O. Геометрический смысл частной производной как r=} (x, y), (x, y) на плоскости х = х0, ось Оу.

• Что касается геометрического значения производной, то из формул (20.20) и (20.9), в данном случае, то есть, если n = 2. Уравнение Является уравнением плоскости, которая проходит через точку (x0, y0, r0) и не параллельна оси Og. As вы знаете, что коэффициенты A и B определяются однозначно из соотношения (20.39、 Итак, плоскость (20.40) однозначно определяется соотношением (20.39).Эта плоскость называется касательной плоскостью для графа функции 2= Таким образом, мы пришли к следующему определению: Определение 6.Плоскость, касательная к графу функции f (x, y) в данной точке такова, что разница между значением этого приложения и функцией f (x, y) бесконечно мала по сравнению с p из p〜0.

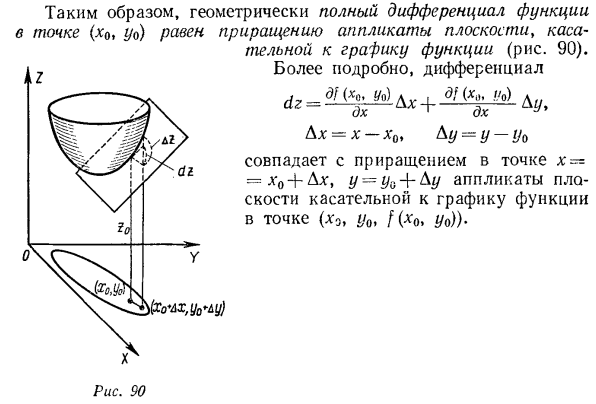
Таким образом, геометрически совершенный дифференциал функции в точке (x0, y0) будет равен приращению приложения плоскости касательной к графику функции. Людмила Фирмаль

• По (20.41) вид уравнений для этой касательной плоскости равен Будущее (т. 2, с. 50.4), мы знакомы с различными подходами к понятию лицевого контакта. Установите Ax = x-x0, Au = y-y0 и запишите правую часть уравнения (20.42) в виде: Это обычная запись для дифференциального π функции r = /(ETA, y) в точках (x0, yo), поэтому формулу (20.42) можно переписать. (рис. 90). Соответствует приращению в точке x = = = 0’0 + DLG, y = yi {Ay. Применение плоской касательной к графу функции точек (x0, y0, [(x0, yv)).

Смотрите также:

Предмет математический анализ

Дифференцирование сложной функции.	Градиент функции.
Инвариантность формы первого дифференциала относительно выбора переменных. Правила вычисления дифференциалов .	Производная по направлению.