Формулы для кривизны и эволюты плоской кривой

Формулы для кривизны и эволюты плоской кривой

Формулы для кривизны и эволюты плоской кривой. В частности, все, что было сказано в предыдущем пункте, относится и к плоской кривой. Заметим, что если кривая Γ= {/•(1)} находится в некоторой плоскости, то все производные векторной функции r (1) также находятся в этой плоскости. plane. In фактически, он содержит приращение векторной функции Ar = r (1 + DO-r (1). Отсюда и родство. Поэтому, легко к R ’= Fr-r этих соотношений находится в указанном plane. In Изменение того же аргумента на r ’ доказывает, что r «находится в той же плоскости. Из вышесказанного следует, что если кривая находится в некоторой плоскости, то касательный вектор r и его кривизна Тогда вектор главной законной линии n находится в одной плоскости.

Следовательно, эта плоскость является контактной плоскостью рассматриваемой кривой. Людмила Фирмаль

• Также, в отличие от§ 17.2, в случае кривой Γ= {/ *(*)} в плоскости xOy, (5) обозначает угол, образованный осью Ox и касательной в точке r (a) (рис.73), а Ya = a (z0-(Ax)-a (xn) становится углом между касательной в точке r (50) и T (50 + A5). Уменьшение с увеличением на 5 =k-золото Предполагая кривую Γ= {/*( * );, запишите некоторые выражения, полученные в предыдущем пункте. a ^ 1 ^ b]является плоским xOy. Р(1)=(х (1), г (1)).Из выражений (17.9), (17.12) и (17.13)、 Из уравнения (17.17), если обозначить центр кривизны кривой Γ как (I, m]), получим формулу для координат. И M] через производную по отношению к x. Кроме того, уравнения (17.19) и (17.20) подразумевают уравнение, представляющее координаты центра кривизны в терминах производной по любому параметру 1.

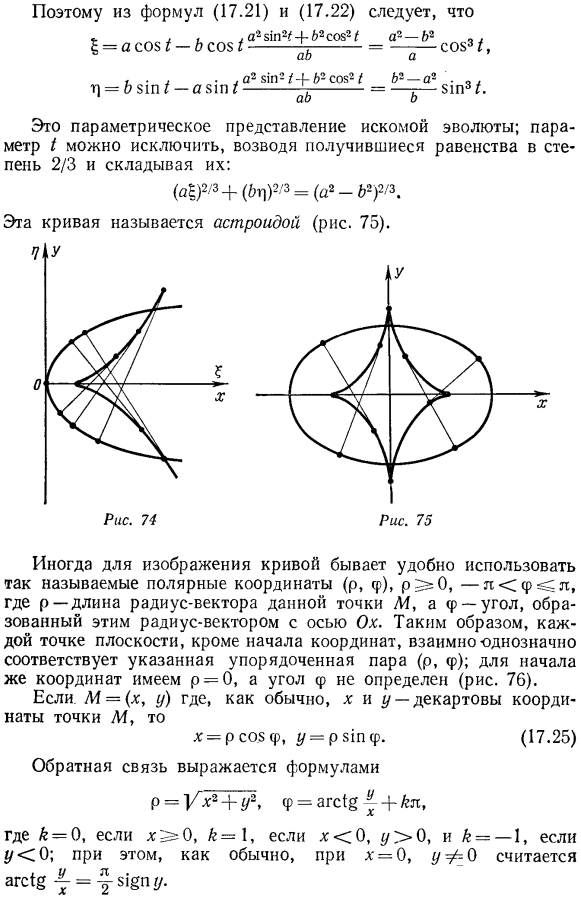
Точно так же Упражнение 1.Пусть Γ-2-кратная дифференциальная плоская кривая без сингулярности, а a-угол наклона касательной к оси Ox. Если кривая представляет собой график функции* / = / ( * ), то формулы (17.20), (17.21) и (17.22) принимают следующий вид: Образцы. 1.Найти кривизну и эволюцию параболы y-ax2. заметим, что y ’= 2ax, y’ ’= 2a, существует k =〜(1-1 {-4a2 2) 3/2 ′ согласно формуле (17.23).чтобы найти уравнение эволюции, используйте формулу (17.24). Результатом является параметрическое представление параболы с параметром x. вы также можете получить явное представление, исключив этот параметр X. To для этого из первого уравнения находим x3 = E / 4a2,а из второго уравнения находим x2 =(2Ac-1)/ 6a2.Если мы квадрат уравнения первого результата, квадрат 2-го с кубом, и выровнять правую сторону, мы получаем.

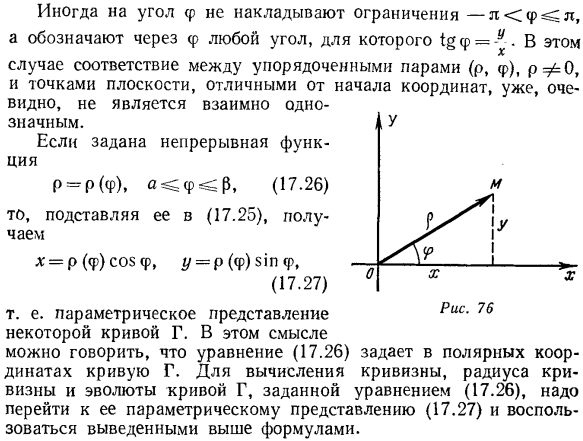
• Эта кривая показана на рисунке. 74, как мы знаем (см. Пример 14.3 из 2), является полукубической параболой. 2. Найти радиус кривизны и эллиптическую эволюцию x = aco& {, y = B $ w/, A> b x ’= aDn/, y’ B cos/, x «= A co8^, y » = B $ m1, по формуле (17.2.0)、 Таким образом, из формул (17.21) и (17.22)、 Это параметрическое представление требуемого Эволюта. Параметр 1 можно исключить, увеличив полученное уравнение до степени 2/3 и добавив его. Эта кривая называется астроида(рис. 75). Иногда для изображения объекта удобно использовать так называемые полярные координаты (p, φ). curve. pE= 0, lCφ ^ l. где p-длина радиус-вектора конкретной точки M, а φ-угол, образованный этим радиус-вектором и осью Ox. Таким образом, для каждой точки плоскости, кроме начала координат, указанная упорядоченная пара (p, f) соответствует 1: 1.Для начала координат он равен p = 0, а угол φ не определен(рис. 76).

Если это так. M =(x, y), где, как обычно, x и y-декартовы координаты точки M. Обратная связь представлена выражением Здесь для x> 0, для k = 0, для K = 1, 0 и для k =0, и для K = −1 (y) 0;в этом случае, как обычно, для x = 0 рассматривается UV 0.И Л АГС. Иногда угол p не накладывается на угол ρ-Φ, но он представляет собой угол p, который равен 1§ф= -* -.С этим В этом случае соответствие между упорядоченными парами (p, p), pFO и точками плоскости, отличной от начала координат, явно не равно 1: 1. Если задана непрерывная функция Затем, если вы назначите его (17.25)、 г. В этом смысле можно сказать, что уравнение (17.26) определяет полярной кривой г в полярных координатах. Используйте выражение (17.27) и приведенное выше выражение.

Другими словами, это параметрическое представление некоторой кривой. Людмила Фирмаль

• Упражнение 2.Приведем кривую p = p (φ) в полярных координатах, a-угол наклона касательной к оси Ox, а o) пусть угол, образованный этой касательной в продолжении радиус-вектора точки контакта. докажите, что a =ω+φ и 1§ω= p / p’. 3.Найти кривую вырождения p = a(1 + cos f), 0 f L. 2-я называется кардиоида. Показания удобно использовать результаты упражнений 1 и 2. Выпуск 13.Пусть Γ-двойная производная кривая без сингулярности, Γ= {r (0; и пусть(0 e [a, b], f | 0 + A> 1e [a, b].? 0 + а / 2е [А, B]. Нарисуйте плоскость через точки r ((0), r (0 0 + A-D и rы 2); в случае кривизны kΦ0 в точках r (0),^> > 0 и^ ^ ^ ^ 0 эта плоскость направлена к плоскости контакта в точках Г (определите это понятие) («) ■ Выпуск 14.Предположим, что предыдущий.

Смотрите также:

Предмет математический анализ

Главная нормаль. Соприкасающаяся плоскость.	Окрестности точек. Пределы последовательностей точек.
Центр кривизны и эволюта кривой.	Различные типы множеств.