Оглавление:







Построение графиков функции
Построение графиков функции. Изучение отдельных функций с помощью аналитического оборудования разработанного нашей компанией и построение его графиков должно осуществляться в следующем порядке: 1.Определяет область существования функции, область непрерывности и точки разрыва. 2.Найдите асимптоту. 3.In проект, создайте график функции. 4. Вычислите 1-ю производную и, при необходимости, вычислите 2-ю производную (производная более высокого порядка часто может быть опущена). 5.Найдите точки, в которых первая и вторая производные не существуют или равны нулю. 6. Создайте таблицу изменений знака для 1-го и 2-го производных. Определить возрастание, убывание, выпуклые интервалы верхней и нижней функций, найти точку экстремума (включая конечную точку) и точку перегиба. 7.Нарисуйте график в конце.
Кроме того, чем выше точность графика, которую вы хотите достичь, тем больше точек вам нужно найти на нем, вообще говоря. Людмила Фирмаль
- Обычно рекомендуется найти (возможно, с определенной точностью) пересечение координатных осей графа с точкой, соответствующей экстремуму функции. При необходимости можно найти и другие точки. Для очень громоздкого представления производной 2-го порядка вам, возможно, придется ограничиться рассмотрением характеристик графа, которые не могут быть изучены без помощи производной 1-го порядка. Пример 1.Построить график функции [(x)= n—. Эта функция определена для всех x ^ 1s и является contiguous. As вы уже знаете (см.§ 14.4), имеют асимптоты y = x-4 и x—1、 Также f (x) x-4; следовательно, f (x) x-4 x-1 (график функции находится выше асимптоты) и/(x) для x-x-1, 4 (график ниже асимптоты).
График функции f(x) пересекает ось Ox в точке x2-3x-2 = 0, то есть в точке xx2 =(3±y17)/ 2, или в точке X1 = 3.5, x2 = 0.5.Ось Oy пересекает график в точке y =-2.Это позволяет построить график функции I (x) в виде, показанном на рисунке. 56. Целью дальнейших исследований является нахождение экстремумов точек перегиба и интервалов, выпуклости верхнего и нижнего графика функции. Для этого мы находим y ’ и y». Х2 + 2х-1 г (х + 1) 2 ’ Из этого x—1 | / A2?Вы можете видеть, что для −2.4 и для x—1 + + Y 2«0.4, y’ = 0.At точка x = −1, производные y ’ и y «не существуют. Отредактируйте таблицу изменения знака 1-й и 2-й производных, включая в нее ключевые моменты, в зависимости от изменения аргументов. Из этой таблицы видно, что функция/(x) имеет строгий минимум в терминах x = −1 + Y ^ 2 и строгий максимум в терминах x = −1-Y2. для Х-1, то функция является строго выпуклой вверх, и для Х-1, то функция является строго выпуклой вниз. при x =-1 функция прерывиста, поэтому точки перегиба нет. Общее поведение функции было следующим found.
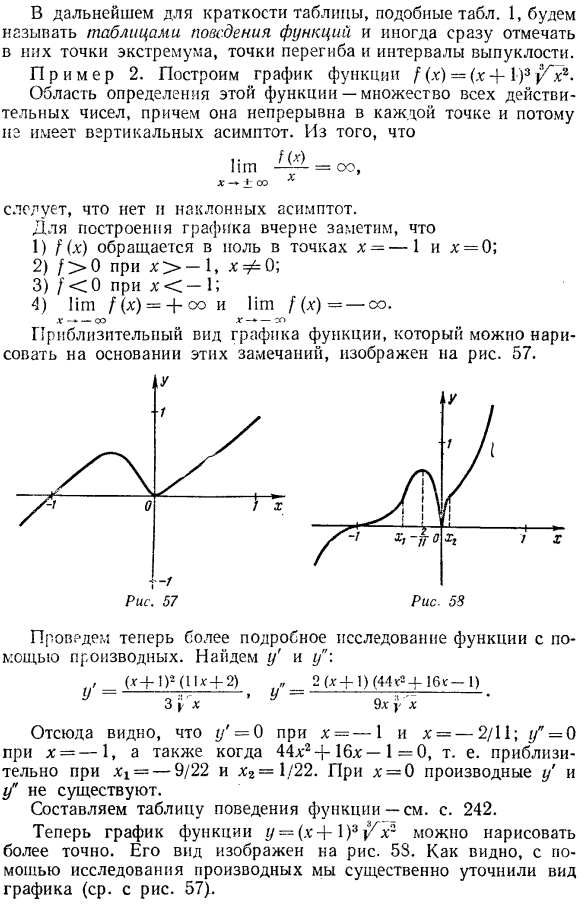
- To чтобы точнее построить график, нужно найти на графике много точек, как описано выше. В дальнейшем для краткости используйте таблицы, похожие на таблицы. 1, вызовите таблицу поведения функции и немедленно отметьте эти экстремумы, точки перегиба, выпуклые точки интервала. Пример 2.Построить функцию) (x)=(x + 1) 3y / r! Область этой функции представляет собой множество всех действительных чисел, причем вертикальных асимптот не существует, так как они непрерывны в каждой точке. От того, что В результате не существует наклонных асимптот. Чтобы построить диаграмму、 1) F (x) исчезает в точках x (-1) и x = 0. 2) x-1 as/ 0, x * 0; 3) / x b-1I при 0 4) ФМ Ф (Х)= + ОО и FM [(х) со. Обзор графиков функций, которые можно построить на основе этих утверждений, показан на рисунке. 57.
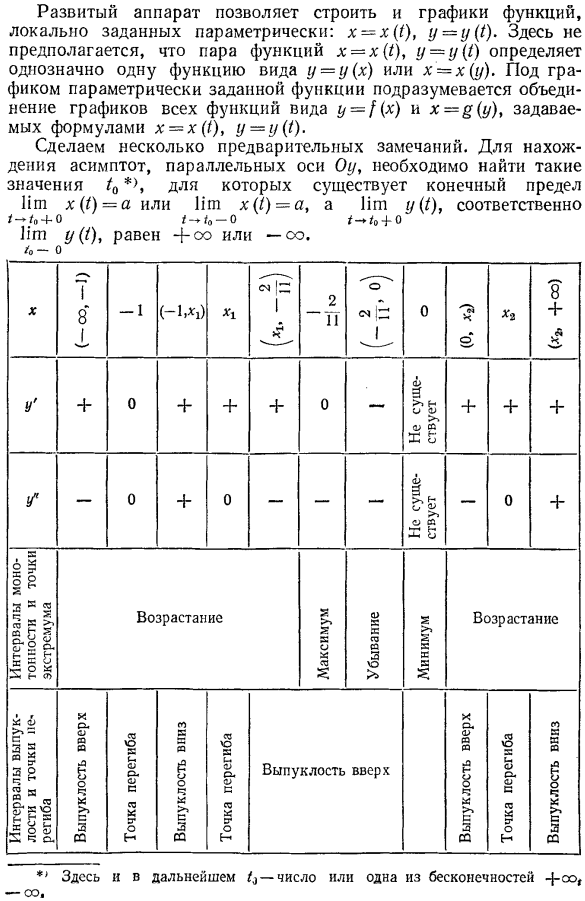
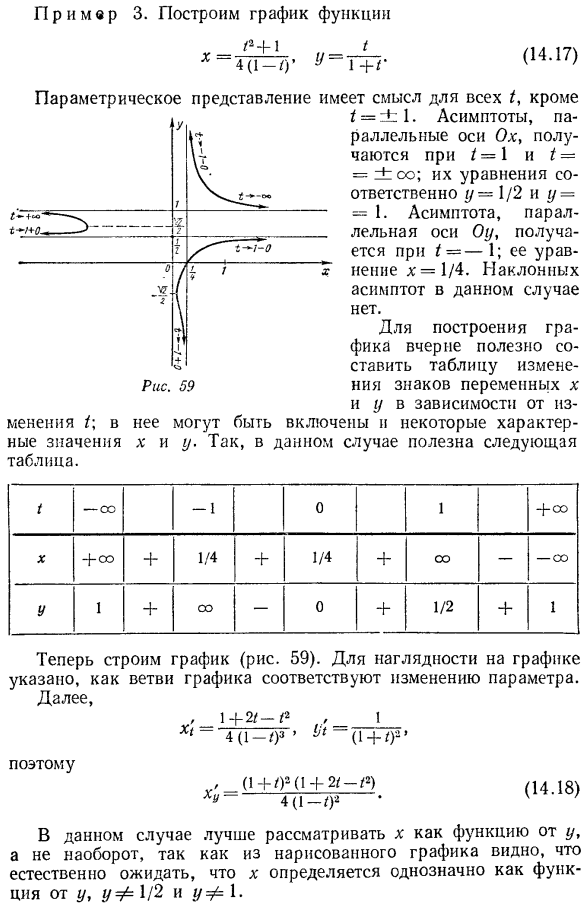
Теперь мы проведем более детальное исследование функции с использованием производных. найти y ’и y.」 Это означает, что x = −1 и y ’ = 0 для x= −2 / 11. если » y » = 0-x—1, а также 44×2 + 16x-1 = 0, то есть xy =-9 / 22 и x2 = 1/2.если x= 0, то производные Y ’и r /’ не существуют. Вижу-P, в котором приводится таблица поведения функции. 242. Теперь вы можете более точно нарисовать график функции y =(x + 1) 3 ^ x3.Его внешний вид показан на схеме. 53.As (см. рисунок 57). Разработанное устройство позволяет строить графики локально параметрических заданных функций. x = x (1), y = y (()здесь пара функций x = x ({), y = y {1) равна y = y (x) или x = x( y).Граф параметрической определяемой функции подразумевает объединение графа всех функций в виде формулы x = x (1), Y = Y ({), Y = Cx) и x =§(y).
Вы можете видеть, что мы использовали исследование производных, чтобы значительно уточнить тип графика. Людмила Фирмаль
- Давайте сделаем предварительное замечание. Чтобы найти асимптоты, параллельные оси Oy, необходимо найти значение*, имеющее конечный предел Если такое начальное значение существует、 х = а(14.14) Уравнение асимптоты должно быть найдено. Аналогично, если мы найдем асимптоту, параллельную оси Ox, мы уменьшим ее до значения определения конечного предела fm y (1) b или fm y (() = b, и fm x (()) 10, где fm () присутствует. Соответственно, Fm x (() равно+ che или-oo. Если окажется, что такое значение 10 существует、 г = Б(14.15) Уравнение асимптоты должно быть найдено. Наконец, чтобы найти асимптоту.
Смотрите также:
| Выпуклость и точки перегиба. | Понятие предела и непрерывности для вектор-функции. |
| Асимптоты. | Производная и дифференциал вектор-функции. |

