Асимптоты

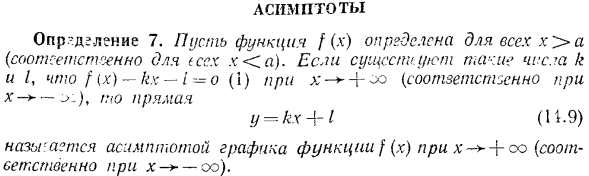
Асимптоты

Асимптоты. Определение 7.Определите функцию f(x) для каждого x a (каждого, каждого Xi). ф(х) кх / = о(1)а + ОО(х-*-о, соответственно. Если есть числа k и мне нравится )、 Называется асимптотой графа функции f (x), а также x〜*—+ co (для x ° ° соответственно). Существование асимптот в графе функции означает, что в случае xco (или-co) функция ведет себя как»почти линейная функция«, то есть она немного отличается от линейной функции. Например, найдем асимптоты графа функции y=•. Разделите числитель на знаменатель согласно правилам деления Терм, y =; s-4.С= О(1） для x-±co прямая y = x-4 является асимптотой графика этой функции как для x ^ + co, так и для x-co. Рассмотрим геометрический смысл асимптоты.

Таким образом, уравнения (14.11) и (14.12) ограничивают задачу нахождения асимптоты (14.9) расчетом определенных видов ограничений. Людмила Фирмаль

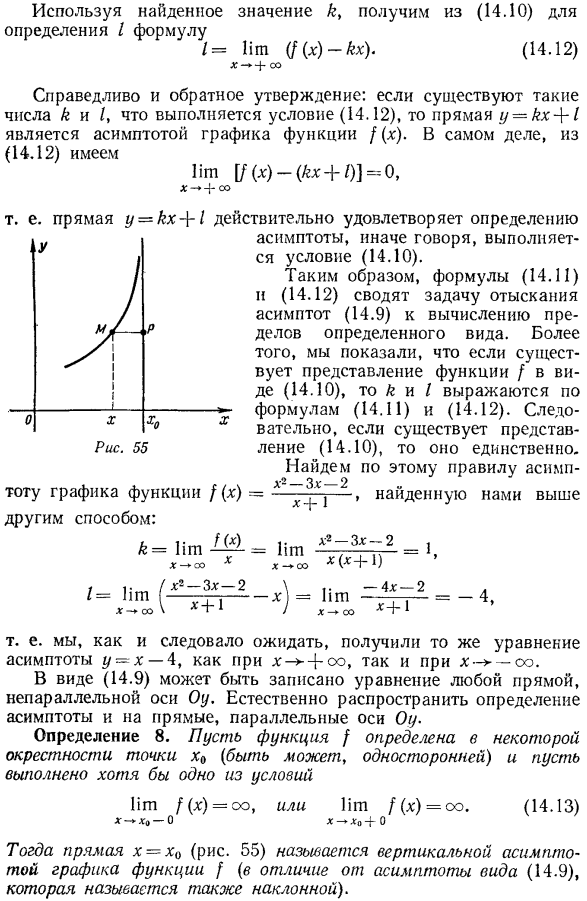
• Пусть M =(x, f (x)) точка графа точки на оси Ox, AB-асимптота (14.9), А b-угол между асимптотой и положительным направлением оси Oh, bΦ -, MR-перпендикуляр, падающий в сетку пересечения асимптоты AB из точки M, прямой Ash и асимптоты AB(рис. Мистер отличается от МО. Только СО80; следовательно, условие м (2-0 и = M’FSO $ b. So ненулевой коэффициент MP-0 x (для x—co, соответственно) эквивалентен. То есть, если тM 2 2 = 0、 То есть асимптота может быть определена как прямая линия, а график функции M, или расстояние от сегмента MR, будет расстоянием, на котором точки M =(x, f (i)) стремятся к нулю, когда они стремятся остаться в графике. «(для Х -} ОО или, соответственно, х-со).

• Мы показываем общий метод нахождения асимптоты(14.9), то есть как определить коэффициенты k и/в уравнении(14.9). для ясности рассмотрим только случай x—(oo (рассуждение для x °°аналогично).Пусть асимптота функции/ ’ S(14.9) равна x-»-(oo. Тогда, по определению、 Разделите обе стороны (14.10) на x и передайте его в предел как x>-+ oo. И затем… Используйте значение k, найденное для определения I из выражения (14.10). Верно и обратное. Если существует такое число k I I, что выполняется условие (14.12), то линия y-kx + 1 является асимптотой графа функции f (x). фактически из(14.12) То есть линия y-kx + 1 действительно удовлетворяет определению Выполняется асимптота, то есть условие (14.10).

Кроме того, мы показали, что k и/могут быть представлены выражениями (14.11) и (14.12), если представление функции/имеет вид (14.10). таким образом, если представление(14.10) существует, то оно unique. By это правило, мы находим асимптоты. Выше мы нашли Функция f totu Graph (x)=по-другому. То есть, как и ожидалось, мы получили одно и то же асимптотическое уравнение y-x-A как для x ^-oo, так и для x-oo. В форме (14.9) можно записать уравнение для непараллельной оси Oy любой прямой line. It естественно расширить определение асимптоты до линии, параллельной оси Oy. Определение 8.Определите функцию в окрестности x0 (односторонней) и определите по крайней мере 1 условие. Золото/(x)=°°, или золото [(x)=°.

Как и в случае наклонных асимптот, для вертикальных асимптот, когда точка уходит в бесконечность вдоль графика, расстояние между точкой и линией стремится к нулю. Людмила Фирмаль

• Тогда линия x = x0(рис.55) называется вертикальной асимптотой графа функции/(в отличие от асимптоты вида (14.9), которая также называется диагональю). при х ^-х0-0 и х-*-хо* −0 Чтобы найти вертикальные асимптоты графа функций, необходимо найти значение такого X. Или оба условия (14.13).Например, функция Y =-является Вертикальные асимптоты x = −1 В общем случае,/(x)= рацион Так как функции ((p (x) и (2 (x)-многочлен), C2 (x0)= 0, P (x0) Φ0), то линия x-x0 является асимптотой графа функции f (x).

Смотрите также:

Предмет математический анализ

Отыскание наибольших и наименьших значении функции.	Построение графиков функции.
Выпуклость и точки перегиба.	Понятие предела и непрерывности для вектор-функции.