Выпуклость и точки перегиба

Оглавление:

Это изображение имеет пустой атрибут alt; его имя файла - image-10-1.png

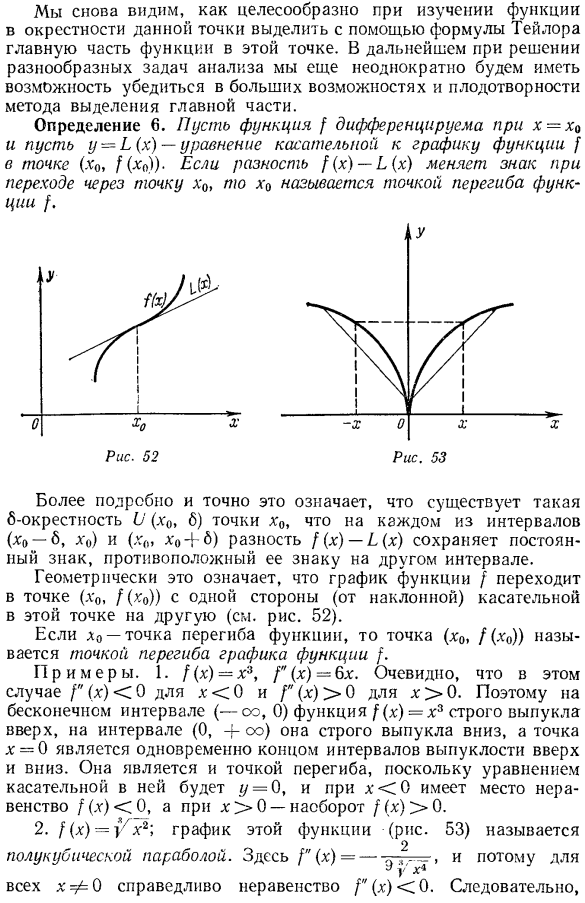
Выпуклость и точки перегиба

Выпуклость и точки перегиба. Определите функцию/в интервале (a, b), andXx .Х2.пусть Б будет. Проведите прямую линию через точки A (x1} (xx)) и B (x2, f (x2)) на графике функции/.Ее уравнение Правая часть этого уравнения представлена 1 (x).Тогда вы можете легко написать: Очевидно, хχχ) = [(XX),/(X2)=определение 3.Функция/, независимо от точек xx и x2, для xx x2 называется вверх-выпуклой (вниз-выпуклой) в интервале (a, b). , Для любой точки x0 интервала (x1} x-2) неравенство Геометрически это означает, что в коде AB нет точки (то есть отрезка прямой y = 1 (x), заканчивающегося в точках A и B Над точкой графика функции/, соответствующей тому же значению аргумента(не ниже) (Рис. 50). Определение 4.Вместо (14.7) и (14.8) выполняется строгое неравенство I (x0)/(A’o), и поэтому для x0, x1 и X% I (x0) /(x0) x2 b функция/ В интервале(А, B) называется строго выпуклой вверх(строго выпуклой вниз).

В этом случае все точки, за исключением концов кода AB, располагаются ниже (выше) соответствующих точек графика функции. Людмила Фирмаль

Определение 5.Интервал, в котором функция выпукла (точно) выше и ниже соответственно, называется (строго) этой функцией, или интервалом выпуклости ниже. Теорема 5 (достаточное условие строгой выпуклости).Функция/является разделом (a, b) для обеспечения 2-й степени дифференциации. Тогда в случае f » 0 на(a, b) функция/строго выпукла вверх, а в случае/» 0 на (a, b) функция/строго выпукла вниз в этом интервале. Доказательство. .Х1.икс. Х2.пусть Б будет. И затем… При применении теоремы Лагранжа (см.§ 11.2)、 Снова применим теорему Лагранжа. Это тот случай, когда/ a есть (a, b), и поэтому, в частности, l (x).！(X), то есть указывает, что функция/является строго выпуклой Вверх; для f » 0 в (a, b), f (x)/(n), то есть функция/выпукла внизу.

Условие постоянства производной 2-го порядка, достаточное для строгой выпуклости (выше или ниже), при этом не обязательно time. So, функция p = n ’4 выпукла строго вниз по целому ряду, но ее квадратичная производная y» = 12×2 исчезает при x = 0. Обратите внимание, что если функция / выпукла на (строго) интервале(a, b), то функция-/(строго) выше этого выпукла на дне. Интервал и наоборот, и-/(x)] = тогда, на В Примере теоремы 5 достаточное условие для восходящей, строгой выпуклости получено из строгого условия достаточности выпуклости нисходящей функции, содержащейся в той же теореме. Упражнение 3.Докажите это для функции Точка π= = 0 не принадлежит выпуклому интервалу выше или ниже и не является концом ни одного из этих интервалов. 4.Докажите, что функция y = x4 строго выпукла вниз по линии целых чисел. мы видим, что выпуклость функции up / down зависит от знака ее производной 2-го порядка. Мы нашли место.

Граф 2 дифференцируемых функций по касательным также в некотором смысле связан со знаком производной 2-го порядка. Теорема 6.Предположим, что функция/имеет 2-ю производную от положительной (отрицательной) через интервал (a, b). / «(x) 0 (соответственно/ » (x) 0), x ^(a, k)*’.Тогда граф точек x0 e (a, b), все точки (x, f (x)), xe (a, b) и функции/расположены на касательной, проведенной в точке (ниже каждой) (A’0,/(A’o)) (конечно, исключение составляет сама эта касательная линия и указанная**) (51). * ’Это означает, что функция/выпукла строго вниз(вверх) до (a, b). * Если функция ’ * ’ I также определена и существует одномерная производная в конце интервала a или b, то это свойство удерживается против касательной точки (a, f (a)), Как видно из следующих доказательств (соответственно, точка (6,/(6))). Фактически уравнение касательной к графу функции/в точке (x0,/(r0)) имеет вид Правая часть этого уравнения обозначается через b (x).

Затем, когда мы применяем теорему Лагранжа к разности/(x)-/(r0)、 Где а. x b, а также между точками| x и x0. Мы снова применяем теорему Лагранжа, но если мы уже применяем ее к приращению производной, мы получаем: Где точка p находится между c и r0. для x ^ x0 это будет (I-r0) (r-r0) 0.Потому что точка§всегда находится между x и r0 и, следовательно, всегда находится на одной стороне точки r и точки r0. Таким образом, знак разности f®-b® совпадает со знаком f » (p) в rΦr0.

Если функция имеет производную 2-го порядка в любом месте любого интервала, то вблизи любой точки в этом интервале основную часть функции/можно выделить в виде полинома 2-го порядка Тейлора. Людмила Фирмаль

Таким образом, если 2-я производная интервала (a, b) положительна (и, следовательно, положительна в точке) p), то для всех xe (a, b), кроме точки r = r0, образуется неравенство f ®-E ® 0;если производная 2-го отрицательна в интервале (a, b), то для всех xe (a, b), кроме точки r = r0, ® 0. Ноль Позвольте мне объяснить эту теорему, основываясь на некоторых других соображениях. / ( * ) = Ф (Хо)+ т (*о) (Х-О)+(У,.) 2 + О((Т-т0) 2), т-го、 Таким образом, график функции.

Смотрите также:

Предмет математический анализ

Признак монотонности функции.	Асимптоты.
Отыскание наибольших и наименьших значении функции.	Построение графиков функции.