Оглавление:











Пузырьковое кипение на горизонтальных и вертикальных поверхностях нагрева при свободной конвекции
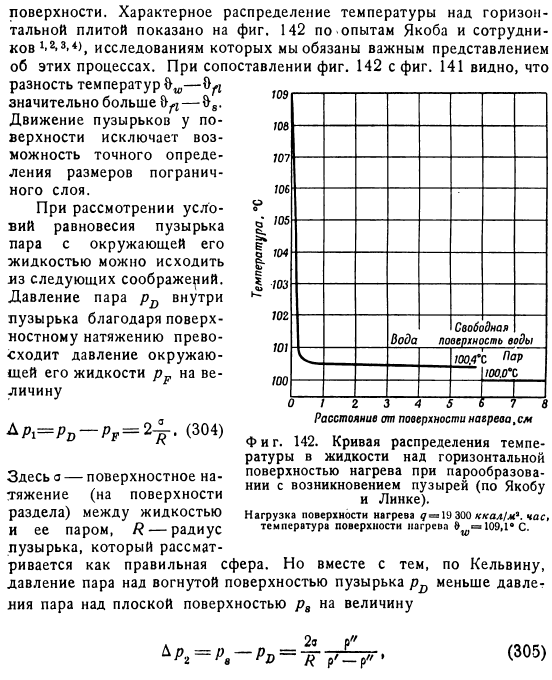
- Как показывают наблюдения, пузырьки пара образуются только на поверхности нагрева, более того, они образуются только в определенных точках, и их количество увеличивается с увеличением тепловых нагрузок. Поверхность. Типичное распределение температуры на горизонтальной пластине показано на рисунке 1. 142 с Джейкобом. Основываясь на опыте сотрудников ML, их исследование обязано важным пониманием этих процессов.
Рисунок 2 142 141 разность температур w значительно больше, чем разброс пузырьков по поверхности, что исключает возможность точного определения размера границы. При рассмотрении условий равновесия пузырьков пара с окружающей жидкостью можно исходить из следующих соображений. Поверхностное натяжение приводит к тому, что давление пара pD внутри пузырька превышает давление окружающей среды. Лицо Где а-поверхностное натяжение на границе раздела жидкости и ее пара, а R-радиус пузырька, который считается правильной сферой. Но в то же время, согласно Кельвину, давление пара над вогнутым пузырьком pD меньше, чем над плоскостью p 306.
В технических подсчетах часто приходится рассматривать смеси водяного пара и двуокиси углерода с неизлучающими газами. Людмила Фирмаль
Где Р и Р-плотность насыщенного пара и жидкости 1.To форма пузырьков, вам нужно перегреть liquid. It имеет давление пара Доктор ДР1, ДРГ. Этому соответствует повышение температуры. Здесь dft dp определяет наклон кривой давления пара. При большом объеме жидкости или идеально гладкой стенке самопроизвольное образование пузырьков пара обычно невозможно в условиях перегрева liquid. In для того чтобы произошло испарение, в центре испарения должны быть пузырьки, шероховатость стенок, накипь. Именно поэтому начальный радиус пузырька имеет конечное значение value.
Нагрузка на поверхность нагрева увеличивается, температура Головки увеличивается, и соответственно В этом случае число центров испарения будет увеличиваться за счет уменьшения в начале начального радиуса R, который необходим для образования пены 2. Около 58,8 Дин см и dit dp, соответствующие 100 C воды, 0,0369 Град 1 мм рт. ст. Из уравнений 306 и 306a мы получаем около Д00, ЗОС, R 103СЛ около R 10 g CM, д 8teз. При испарении в установившихся условиях температура стенки может быть значительно выше, чем на Рис.1.Это неудивительно, поскольку необходимо учитывать процесс теплопередачи по теплопроводности от поверхности к сердцевине текучей среды через область стенки.
Пузырьки пара, образующиеся на стенках, растут в результате дальнейшего испарения вглубь помещения. Это будет продолжаться до тех пор, пока не будет достигнут определенный предел, после чего пена выйдет и поплывет. Этот предельный объем, определяемый Башфор и Адамс9 как функция угла контакта p, представлен Фрицем в безразмерном виде form. In эти соотношения, так называемая постоянная Лапласа, являются параметром Например Этот расчет, путем обработки кадра неподвижного изображения на фиг.
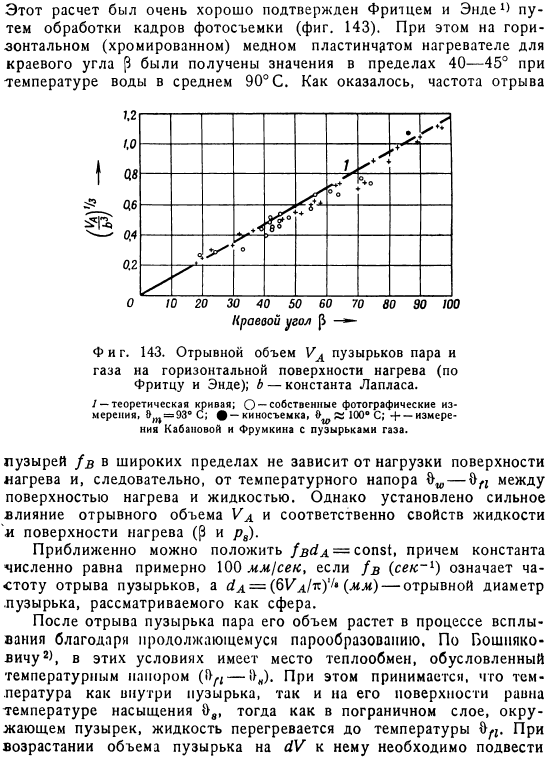
Было подтверждено очень хорошо Фришем и Эйде1. 143.At тогда же был получен горизонтальный хромированный медный пластинчатый нагреватель под углом Р края, при средней температуре воды 90 с, равной 40-45. Икс- Икс Около 10 20 30 40 50 60 АО 100 Угол контакта Р Тоже фигура. 143.Ул громкости отрыва пузырька пара Н Фриц и Эйде б-постоянная Лапласа. Широкий диапазон пены не зависит от нагрузки на поверхность нагрева, а следовательно, и температурный напор-не зависит от нагрузки между поверхностью нагрева и жидкостью. Однако установлено сильное влияние разделенного объема U1, следовательно, свойств р и 8 жидкости и поверхности нагрева.
Приблизительно vyl-const можно поставить, константа численно равна примерно 100 мм в секундах, что означает частоту разделения пузырьков в секундах, а 4l 6Ud1k 1 мм — это диаметр разделения пузырька, рассматриваемого как сфера. После отделения паровых пузырьков их объем увеличивается, так как во время процесса подъема пар продолжается. По данным Bosnyak-vich2, в этих условиях происходит теплообмен с температурным напором ft. Кроме того, мы предполагаем, что температура как внутренней части пены, так и ее поверхности равна температуре насыщения 9, но в пограничном слое, окружающем пену, жидкость будет перегреваться до температуры L1.
Как dV увеличивает объем пузыря Значение Рузок Поверхность. Таким образом, теплопередача на первом этапе осуществляется теплопередачей в жидкость. Пузырьки пара влияют на гидродинамику этого процесса, но даже если пузырьки находятся на поверхности нагрева, подвод тепла к ним происходит полностью за счет теплообмена с жидкостью. По мере увеличения Из-за тепловой нагрузки q поверхности увеличивается перегрев стенок, и по данным-s появляется новый центр испарения. Перегрев жидкости относительно парового пространства L не зависит от q в широком диапазоне.
Частота выделения паровых пузырьков и их объемное разделение, а следовательно, и интенсивность испарения у конкретного поверхностного элемента зависят в первую очередь исключительно от характеристик жидкости и стенок. Согласно этим соображениям, избыточная температура стенки по сравнению с жидкостью служит характеристическим температурным напором теплопередачи process. So, в дальнейшем коэффициент теплопередачи определяется следующим уравнением Я Если вы явно не укажете другие определения. Якоб и соавтор 1 эксперимента в кипящей воде при 100 С, рис. 145, показывают наличие кривой A f q из 2 областей, разделенных четким изломом-в момент тепловой нагрузки.
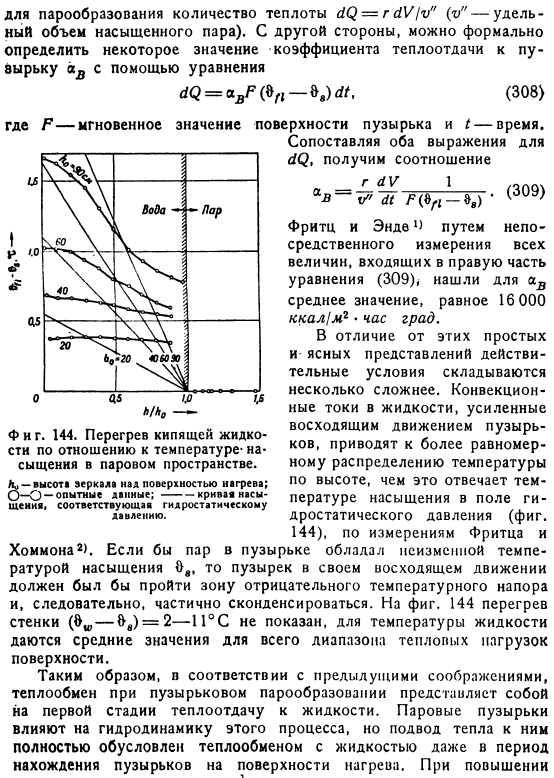
Q 15,000 ккал 1 мг в час только небольшое количество паровых пузырьков formed. So, как показали Якоб и Линке2, весь процесс может быть определен уравнением Nu const GrPr. Это полезно для свободной конвекции в турбулентных пограничных слоях. График на рисунке, 145 соответствует уравнению 152d-2, ккал-мг-время града Где q выражается в Ккал м2 времени. По мере того как нагрузка увеличивает, нарушая влияние пузыря пара будет очень сильным, которое изменяет природу process. In в этом случае основную роль играет процесс в пограничном слое поверхности нагрева. Там, под влиянием отделения пузырьков воздуха, возникает сильное локальное течение.
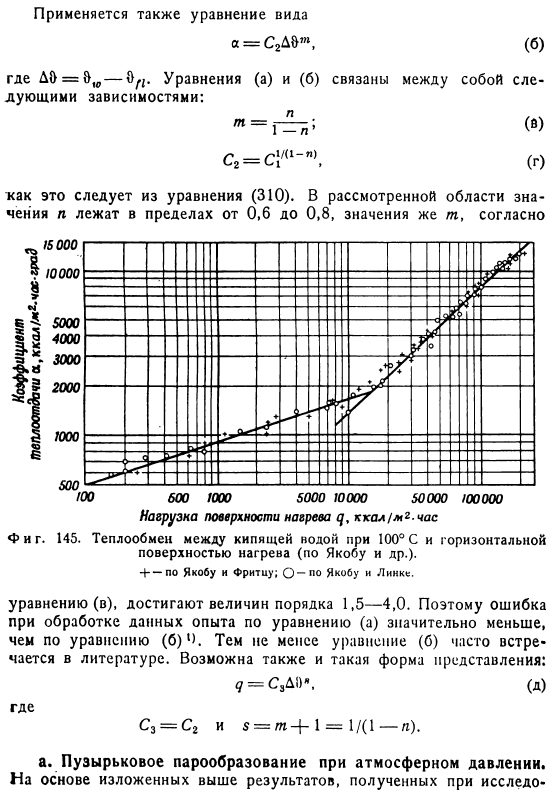
Эта область является наиболее важной для технологии, которую в будущем следует рассмотреть более подробно. Этот раздел ограничен случаем естественной конвекции жидкости, кипящей в горизонтальной и вертикальной нагревательных поверхностях в контейнере, который не слишком мал по объему. Данные опыта лучше всего представить в виде обычного степенного закона Но… График, показанный на фиг. 145. ЗП Но… Также применяется уравнение вида СГДt. Здесь, 8-0.Уравнения a и b связаны путем генерации зависимости б Между ними Восемь огрей q, ккал МЗ-час По словам Якоба и других, 100 C вода и горизонталь.
Уравнение с достигает значения порядка 1,5-4,0.Таким образом, погрешности обработки экспериментальных данных по формуле а значительно меньше, чем по формуле В Н, но в литературе формула В встречается чаще. Такой формат презентации также возможен. 9 С Д Д C, Cr, и-1 1-L. К а. испарение пузырьков воздуха при атмосферном давлении, основанное на приведенных выше результатах, полученных в результате исследования При образовании и подъеме парового пузыря Якоб и Линк смогли получить следующие безразмерные уравнения Три тысячи сто двадцать один Где b-постоянная Лапласа из уравнений 307 и 143, явно связанная с объемом отрыва и, следовательно, диаметром отрыва 1d.
Поэтому функция dA используется в качестве size. In кроме того, p и g представляют собой плотность насыщенного пара, а следовательно, и теплоту испарения, K-теплопроводность жидкости. Для переменных это определенное количество опыта с измерением скорости. Целесообразность использования этого количества обусловлена примерным постоянством продукта fgdA cf. С. 415. за величину w Якоб и Линке взяли цифру 280 м часов, полученную в результате экспериментов с водой и четыреххлористым углеродом. Нижний предел применимости Формулы Это значение Q в точке разрыва кривой на фиг. температура. из рис. температура. 145.Для верхнего предела применимости уравнения 312 С. 42. См. сноски на стр. 1 из 414.
Аналогичный подход к решению проблемы V. I. It был принят в произведения искусства. Рубински. Сборник научных трудов Института теплоэнергетики Украинской Академии наук, Т. 5, 71-83 в 1952 г. К уравнению Ну К, РГ. Моя книга Мой GF РВ Нагрузки и самостоятельной a. At при этом учитываются изменения w, обусловленные давлением. Л. М. Некоторые соображения по поводу результатов, полученных Зысиной…… жидкости и их кинематографические исследования. Техн, архив ЦКТИ, 1939, эффект давления выражается зависимостью Где индекс 0 указывает на значения, связанные с атмосферным давлением.
- Обработка очень большого количества экспериментального материала приводит к определенной форме опорного уравнения Nu 54 1 VR. Значение Формулы, главным образом, заключается в том, что она является первым обоснованным уравнением теплопередачи при образовании пузырьков. Она полностью покрывает результаты исследований с водой и другими жидкостями при давлении 760 мм рт. ст. Искусство. Исходя из значения, полученного в среднем по экспериментам с водой 100 с, Фриц достигает эмпирической Формулы 2. 1,480 из них на 313a И 4. 80 Д8.
Три тысячи сто тридцать шесть Большое значение имеет влияние старения на коэффициент теплопередачи, открытый Якобом и его коллегами, а также влияние шероховатости на установленную ими интенсивность теплопередачи. Длительные эксперименты, длящиеся от нескольких часов до нескольких суток, приводят к уменьшению количества адсорбированного на поверхности воздуха и, соответственно, количества активных центров испарения. Из-за этого такая же нагрузка на поверхность нагрева потребует большего перегрева. Нагретая поверхность с искусственной шероховатостью сначала дает высокое значение, но со временем оно также уменьшается.
Это можно учитывать путем введения поправочного коэффициента, меньшего единицы, на который надо умножить степень черноты, если парциальное давление меньше 1 ат. Людмила Фирмаль
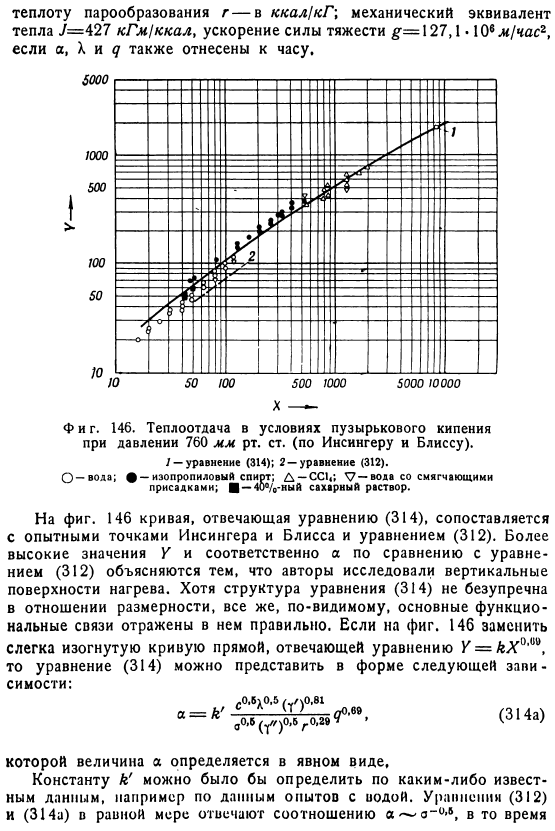
Этот эффект влияния времени может частично объяснить наблюдаемое сильное рассеяние экспериментальных данных. Основываясь на обширных и тщательных исследованиях испарения пузырьков, Инсингер и Блисс 3 пришли к следующему уравнению в безразмерной форме, которое они считали применимым при давлении 760 мм рт. ст. Искусство. Журнал г 0.363 0.923 журнала х-х г 0.047 журнала. Триста четырнадцать Y — — — — — — — C. Десять мне, РВГ в 10. Например, необходимо соблюдать следующие единицы измерения, поскольку формула 314 описана в технической системе безразмерных величин и единиц. Удельный вес пара и жидкости f и q составляет кг м3, поверхностное натяжение-кг кг, а теплоемкость жидкости-ккал кг-град.
Теплота испарения г-ккал кг, механический эквивалент теплоты составляет 7,427 кг ккал, ускорение свободного падения г 127,1 ум раз Икс Давай посмотрим. Блаженство из более точного уравнения 314 Как певец. В любом случае влияние поверхностного натяжения на это соотношение верно и почти определено. Инсингер и Блисс, в отличие от Джейкоба, не наблюдали старения коэффициента теплопередачи.
Возможно, это можно объяснить тем, что они работали с оборудованием, которое было особенно тщательно очищено и полностью очищено от жидкости. Для 100 с воды в области, где пузырьки кипят, процесс испарения идет относительно хорошо studied. So, естественно, возникла идея перехода на относительный коэффициент теплопередачи всех жидкостей при давлении 760 мм Hg. Art. As делается в таблице, по отношению к воде. 32, Фриц 2 Таблица 32 Коэффициент теплопередачи a образования пузырьков относится к величине ay воды при той же нагрузке на поверхность нагрева при давлении 760 мм рт. ст. Искусство. 10 Na, SO4. 20 раствор сахара 40 26. погружной глицерин 55.
Изопропиловый спирт, метиловый Керосин. Четыреххлористый углерод Н-бутиловый спирт 0.70 0.53 0.52 0.36 0.35 0.32 b. влияние давления пара. Предыдущие соображения по испарению при атмосферном давлении. Однако рассматриваемое уравнение может быть применено и к другим давлениям. Якоб дал обобщенную форму уравнению 312. 315. Здесь индекс а обозначает величину, связанную с атмосферным давлением, b-постоянную Лапласа по формуле 307, как упоминалось ранее.
Формула 315 с учетом Бониллы и Перри 2 Используя данные их экспериментов на воде, этиле и бутиле Власть Спирт, ацетон, некоторая 2-компонентная смесь, измененная следующим образом Здесь, число Прандтля PR присваивается жидкости в состоянии кипения. Область исследования имеет значение Pr от 1 до 12 и давление от 0,2 до 1,5 Ат. Для двухкомпонентной смеси было получено значение а между значениями чистых компонентов. Верхний Функция нагрева была горизонтальной хромированной пластиной. Влияние стресса может быть выражено в отношениях Где индекс Р относится к давлению пара р в Ат, а индекс о относится к атмосферному давлению 1 Ат.
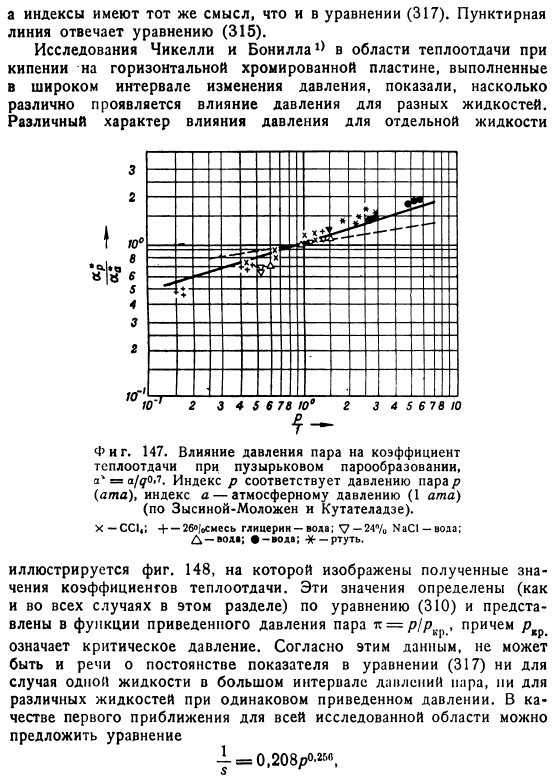
Insinger и Bliss4 предложили значение 0,4 для показателя этого уравнения, в то время как Fajani11 рекомендовал значение 0,27. Зысина-Моложен и Кутателадзе11 также исправили уравнение Якоба 315, но зависимость постоянной Р 1л от давления была специально изучена. На рис. 1 147 показано соотношение a a в зависимости от давления a и A l в зависимости от давления a Индекс имеет то же значение, что и выражение 317.Пунктирные линии соответствуют формуле 315.
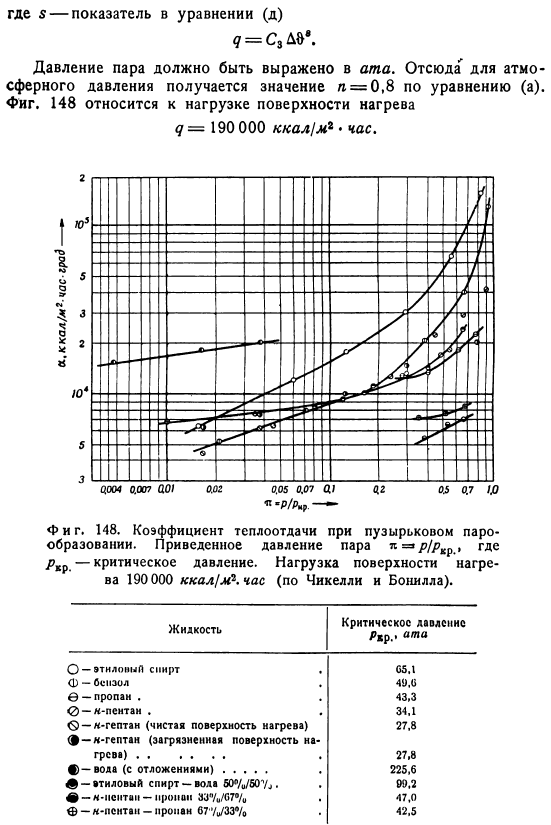
Исследования чичери и Бониллы в области теплопередачи Горизонтальный хром пластины Кипеть В широком диапазоне изменения давления мы показали, как различаются эффекты давления для различных жидкостей. Различные свойства влияния давления на одну жидкость Рисунок 2. 148 показывает результирующее значение коэффициента теплопередачи. Эти значения определяются, как и во всех случаях в данном разделе, в соответствии с уравнением 310 и выражаются в виде функции уменьшения давления пара до р, Где Р означает критическое давление.
Согласно этим данным, ни для одной жидкости с широким диапазоном давления пара, ни для разных жидкостей с одинаковым пониженным давлением не может быть никаких проблем с постоянством показателей уравнения 317.As в начальном приближении можно предложить уравнение для всей исследуемой области. 0.2080202 Где S-показатель степени уравнения д 9 С, Л. Давление пара должно быть представлено формулой ata. So, при атмосферном давлении, величина Р 0,8 получается по формуле А. Также рис. 148 относится к нагрузке на поверхность нагрева 9 при 190 000 ккал м.
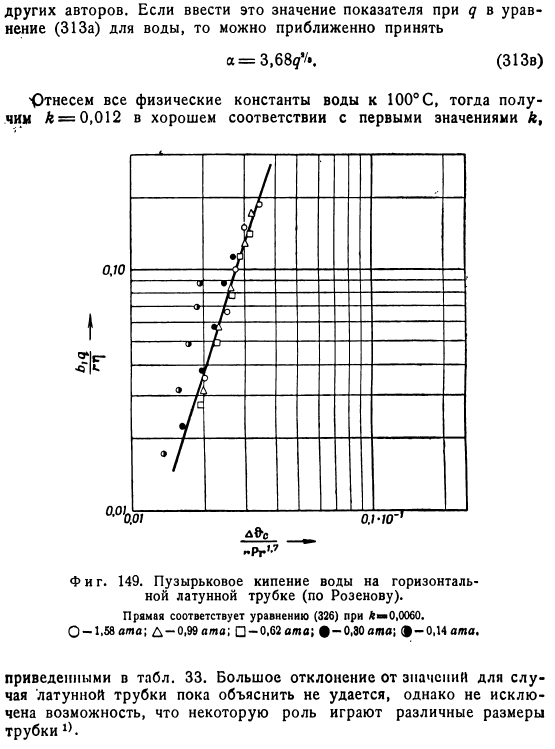
Общая значимость тщательного изучения пузырькового кипения Джейкобом и его коллегами, а также общие выводы, которые Джейкоб сделал на их основе, особенно проявились в дальнейшем развитии теории розеноффа. Розенов вводит некоторое число Рейнольдсов на поверхность нагрева, в которой возникают пузырьки. На основе уравнения Бога 2 Р-в- Где в-плотность потока пара, чтобы быть отделены друг С пеной от поверхности Отопление в единицу времени Триста восемнадцать На единицу Площадь, например кг м2 время, да-диаметр отрывного пузырька паровой пар м и т-это динамическая вязкость температуры кипения, а температура насыщения е выражается в кг м времени.
Плотность потока пара Ov Fflf ов НФД в р л они Триста девятнадцать Где n-число центров испарения на единицу поверхности —частота выделения пузырьков Vx ixit 6-объем отрыва. Рисунок 1 143 получаем соотношение да сопи в 320 Где p-краевой угол пузырька на поверхности нагрева, b1 и b2-модифицированная постоянная Лапласа, формула 307.С другой стороны, нагрузка на нагревательную поверхность q и разделенный объем Vx q const rp nfVA, 31 321, где постоянная зависит от давления пара. Уравнение 321 содержит предположение, что при нахождении на поверхности пузырь пара будет снабжаться всем количеством тепла, а следовательно, последующее испарение во время затопления будет незначительным.
Исходя из Формулы 319-321, число Рейнольдса можно представить в виде 322. Из этого уравнения видно, что в процессе испарения поверхностная нагрузка q играет важную роль. Таким образом, была некоторая основа для ранней формы выражения f Q. В свою очередь, число нуссельта определяется методом Якоба 323. В отношении выражения 320 можно также написать 323а. Согласно ранее упомянутой концепции, тепло от поверхности нагрева сначала передается жидкости. Поэтому число Прандтля этой жидкости вводится как еще одна переменная.
Полученная здесь зависимость также применима к случаю поверхностного кипения переохлажденной жидкости 11, поэтому коэффициент теплопередачи здесь называют температурным напором A8-8W-8. если мы заменим q-AD8 При температуре стенки 8С температура насыщения. Поэтому эта формула определяет зависимость между энтальпией перегрева жидкости и теплотой испарения. Угол соприкосновения пузырька пара p является жидкой фазой p.
Смотрите также:
| Смеси паров с инертными газами и смеси конденсирующихся паров | Пузырьковое кипение в вертикальной трубе |
| Испарение со свободной поверхности жидкости без образования пузырей | Пленочное кипение |

