Оглавление:








Теория пленочной конденсации по Нуссельту
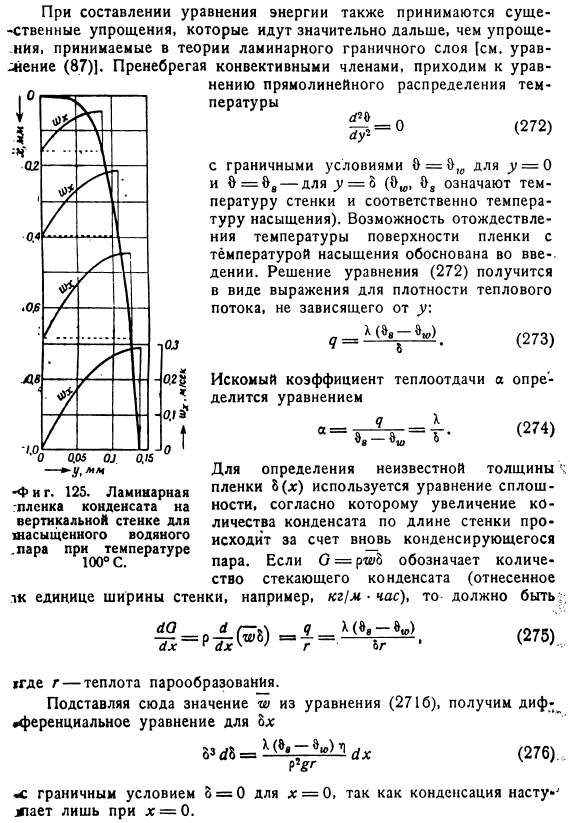
- Нуссельт начал с концепции чистой мембранной конденсации в слое движущегося конденсата. В случае неподвижного или медленно движущегося пара поверхностный импульс и сдвиговое напряжение на границе раздела пара и конденсата могут быть проигнорированы. Поскольку пленка воды очень тонкая, силой инерции также можно пренебречь. Поэтому необходимо уравновесить силы притяжения и внутренние friction. Кроме того, игнорируя кривизну поверхности пленки, можно рассматривать только движение в направлении оси Х фиг. 125. Поэтому речь идет об уравнении движения пленки в вязком режиме, так что давление в пленке остается постоянным и равно давлению пара.
Таким образом, когда пленка воды движется вдоль вертикальной стенки, формула 19 значительно упрощается w заменяется W. через g-g. граничные условия описываются в стенке y 0 в следующем виде t, внешняя поверхность пленки A толщина, пленка DW DY то есть, согласно первому предположению, внешняя сила не действует на внешнюю поверхность пленки. Решение уравнения 271 получается в виде О средней скорости Г. ФГ ЗП 271а 2716. Скорость движения поверхности пленки при 8 равна массе 1,5 Ш. При составлении уравнений энергии также принимается гораздо большее существенное упрощение, чем упрощение, принятое в теории ламинарных пограничных слоев.
Однако теория позволяет также вычислить пространственное распределение испускаемого излучения, причем результаты вычисления хорошо согласуются с экспериментальными данными и, таким образом, приводят к соотношениям, указанным. Людмила Фирмаль
Увидеть выражение 87.Если пренебречь термином конвекции, то получим уравнение линейного распределения температуры 272. 274. Требуемый коэффициент теплопередачи а определяется по формуле Я х 8, −8 y 0 9 9 9 OE граничные условия-Y 8 9I, граничные условия 9 означают температуру стенки и, следовательно, температуру насыщения. Возможность идентификации температуры поверхности пленки при температуре насыщения обоснована в разделе II. решением уравнения 272 является уравнение плотности теплоты Для определения неизвестной толщины H пленки 8 x используется непрерывная формула. Это приводит к увеличению количества конденсата по длине стенок за счет вновь сконденсированного пара.
Если Орш8-1K единица ширины стенки, например кг м, это указывает на количество конденсированной воды, протекающей, называемое временем 275. Здесь r-это теплота испарения. Здесь мы подставляем значение w в уравнение 2716 и получаем дифференциальное уравнение 8×8 секунд dl dx 276.. Поскольку конденсация происходит только в x 0, граничное условие x 0 равно 8 0.
Решение имеет следующий формат Принимая во внимание уравнение 274, локальное значение коэффициента теплопередачи в точке x равно ГУС ХИДДИНК, −1 278. И так оно и есть. Для среднего значения коэффициента теплоотдачи от Х 0 до Х ч, г 279. Здесь 0.943 4 Z. согласно заключению, все физические константы связаны с конденсатом, и лучше всего принимать значения, соответствующие 81H 8, — 8i, 2. уравнение 279 может быть выражено в безразмерной форме, если построить число нуссельта, используя среднее значение и высоту H из a, то есть ия, ahx. Второй В оригинальной работе у Нуссельта 1916 года использована техническая система агрегата.
Затем плотность p кг l9 заменяется, например, удельным весом в кг м секунд кг-второй ЛР 279а. к-мг г-мм, — о Здесь фактор 7.3 уже не является безразмерным. I. сравнение уравнений 279 и 279а доказывает известное неудобство использования технической системы агрегата. Уравнение 279 может быть использовано непосредственно для процессов, имеющих различные значения ускорения, например, путем простой замены g на o во вращающейся системе. Для выражения 279a это не принимается. — Примечание автора Критерии подобия теплопередачи при конденсации чистых паров, полученные на основе теории безразмерной комплексной аналогии, представлены в справочнике 1.S. 8, появляясь в пьесе Тревелла. Кутате С. С.
Теплообмен с изменением агрегатного состояния вещества. Основа теории. Машгиз, 1939, и теплопередача n в момент конденсации. Кипяток, зефир, 1949 и 1952.Эд. Впервые в 1935 г. Однако безразмерное представление уравнения Рейнольдса водной мембраны более очевидно. Двести восемьдесят один Если переохлаждением конденсата до температуры насыщения 0 можно пренебречь, то отводимое тепло можно также выразить в следующей форме с количеством конденсата O О, Н. Вот почему у меня есть отношения с Леном. 281а Лия. — М н Ри Две тысячи восемьсот шестнадцать Это относится к любой конденсации мембраны, независимо от предположения ламинарности течения водной пленки.
Уравнение 2816 позволяет уравнению 279 быть представленным в следующей безразмерной форме ч, 1 282. Это уравнение используется позже при рассмотрении турбулентной пленки воды. Выражение 282 также может быть преобразовано в следующий формат это часто встречается в американской литературе 1. К. Одна тысяча двести восемьдесят два Здесь, после замены v iilg г-0.925 Ре 7. Две тысячи восемьсот двадцать шесть Уравнение ty g 1 имеет размерность длины, поэтому левую часть уравнения 2826 можно официально считать числом нуссельта. В американской литературе… —————- р. .. …………. 4х заново В качестве определенного размера принимается диаметр, отличный от толщины. — Прим, перев.
Можно безразмерного представления описаны в работе Traupel. В. TgarepI Allg. Warmetechnn.4, 1015-107, в 1953 г. Вывод на сегодняшний день актуален в случае вертикальных стенок или вертикальных труб, диаметр которых не слишком мал. Если стена наклонена под углом 3 градуса относительно горизонтальной плоскости, то вместо 271 получим следующий вид уравнения движения 271 дюймов —- ССБ.- При всех прочих равных предположения, коэффициент теплоотдачи a определяется из этого.
- Это связано с вертикальной стенкой с помощью уравнения 279 от зависимостей. Двести восемьдесят три Однако этот пересчет действителен только для чистой пленочной конденсации. Нуссельт также предлагает методику расчета теплопередачи горизонтальных труб. Дифференциальное уравнение толщины пленки в этом случае графически интегрируется. Если и-длина трубки, то ad — ее длина. Наружный диаметр, затем горизонтальное положение Двести восемьдесят четыре Кроме того, опять же, определяется уравнением 279.Так, например, в Н3 м и Д 0,029 м, мы находим ей-богу. 2.5 таким образом, при горизонтальном расположении трубы она конденсирует пар в 2,5 раза больше, чем при вертикальном расположении трубы.
Если n труб выровнены вверх и вниз в горизонтальном пучке, коэффициент теплопередачи нижней трубы уменьшается в предположении согласно уравнению 274, поскольку водяная пленка нижней трубы утолщается за счет оттока конденсата из верхней трубы. Тот. Все остальные предпосылки остаются. Из всех n труб в качестве среднего значения коэффициента теплоотдачи получаем значения, определенные из соотношения s c C C C C J, согласно уравнению 284.Где а-коэффициент теплопередачи самой верхней трубы.
Это соотношение не всегда может быть использовано, так как для промышленных материалов показатели преломления обычно неизвестны. Людмила Фирмаль
Однако недавние исследования показали, что рассматриваемый эффект не возникает даже в случае горизонтальной коридорной балки, состоящей из 25 рядов, а высота коэффициента теплопередачи остается постоянной и равна коэффициенту теплопередачи верхней трубы. Потому что капли конденсата, которые падают на пленку, очень турбулентны Это фактически компенсирует увеличение термического сопротивления пленки за счет утолщения 1. Как отметил Шмидт, открытие нуссельта может быть также применено к конденсации внутренней поверхности горизонтальных трубок и контейнеров.
На практике температура стенки не остается постоянной, как это было принято в граничных условиях уравнения 272.Охлаждающая вода, которая течет вдоль поверхности конденсатора, заметно горячая, поэтому плотность теплового потока может быть выражена — М.- Где L fe l a-f s X C, an-коэффициент теплопередачи со стороны жидкости, s-толщина стенки, а Xu — теплопроводность стенки. Можно предположить, что коэффициент теплопередачи постоянен, но температура стенки и температура жидкости зависят от X.
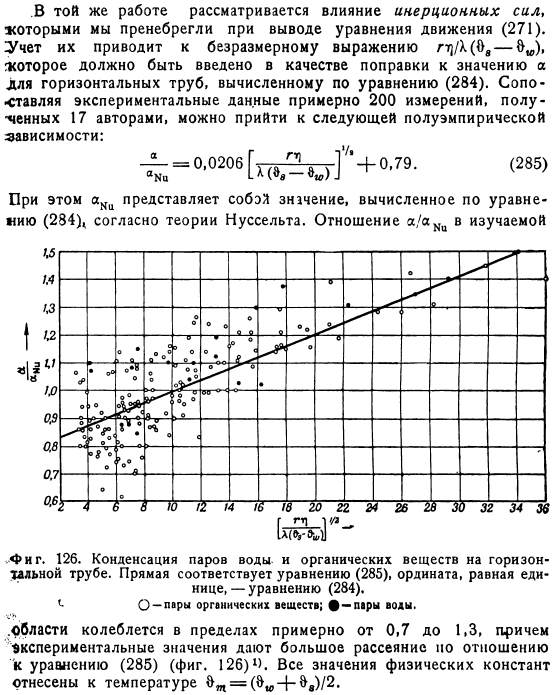
Использование средней температуры стенки можно считать очень разумным, так как точный расчет вносит очень небольшую поправку в Формулу 279.Peck и ready, которые также учитывали тепловое сопротивление труб, дали аналогичный результат в случае горизонтальных труб. В этой же работе рассматривается влияние сил инерции, которым мы пренебрегли при выводе уравнения движения 271.Учитывая их, она рассчитывается по формуле 284d безразмерной формулы ri k O, которую следует ввести как поправку на величину A в горизонтальной трубе-и привести к. Сравнивая экспериментальные данные около 17 200 измерений, полученных авторами, можно выделить следующие полуэмпирические МЕ- Тоже фигура.
Конденсатная труба. Пиар Области экспериментального варьирования………… Рис 126 4.Все До температуры. 2 февраля. Кружилин 11 исследовал ламинарную пленку воды на основе уравнений теплового потока и импульса. См. стр. 267.Он ввел линейное распределение температуры и параболическое распределение скорости в эти уравнения, уравнение 271a. уравнение 271a также применил Нуссельт, поэтому полученные результаты не очень отличаются. При составлении уравнения теплового равновесия уравнение 275 предполагалось, что тепло, выделяющееся при конденсации поверхности пленки, также отводится непосредственно на поверхность пленки.
Дело в том, что конденсированные частицы должны быть такими supercooled. As она прогрессирует, проникает в область низкой температуры, внутрь воды film. As в результате линейное распределение температуры слегка изгибается вверх, так что к стенке отводится больше тепла, чем выделяется во время нагрева. condensation. To определив влияние этого явления, связанного с конечной теплоемкостью конденсата, бромлиг предлагает уравнение Двести восемьдесят шесть Где c — теплоемкость конденсата, а aNn определяется уравнением 284.In типичные условия технологии, Формула E, — имеет мало r, и эти поправки достигают значений, которые важны.
Сумма переохлаждения конденсированной воды может быть рассчитана по формуле нуссельта. При линейном распределении температуры и параболическом распределении скорости средняя температура конденсированной воды, протекающей через вертикальную плоскость, определяется следующим уравнением Учитывая изменение температуры стенки, Киршбаум получил численный коэффициент 9, вместо 3 8, вместо 0,55-среднюю температуру стенки. Сравнение экспериментальных данных и теории. Если теоретические предположения действительно удовлетворяют ламинарной пленке конденсата, то экспериментальные данные хорошо согласуются с отдельными выводами из уравнения 279, например, соотношением 2.
Что касается абсолютного значения коэффициента теплоотдачи, то здесь, наоборот, экспериментальные результаты дают заметное отклонение от теории, что легко видно в случае U горизонтальных трубок на Рис.1. 126 3.Для вертикальной стенки ошибкой является принятие того, что значение а, найденное экспериментально, дает отклонение 279 от значения, определенного уравнением 10-20.Исправления, описанные в предыдущем разделе, недостаточны для объяснения.
Смотрите также:
| Расчетные формулы для свободной конвекции | Образование волн на поверхности пленки |
| Теплоотдача при конденсации | Смешанная конденсация |

