Оглавление:








Дальнейшее развитие теории Рейнольдса и Прандтля
- Обратная сторона аналогии Рейнольдса в условиях течения под давлением и в случае Pr-1 была количественно определена Тейлором. Один из профилей температуры он рассчитал в случае течения, когда происходит падение давления, оно отклоняется на несколько процентов от профиля скорости, найденного в эксперименте. Это отклонение заключается в том, что температура стенок повышается . Таким образом, результаты, полученные Тейлором, согласуются с выводом, который привел к методу Прандтля источников тепла. Уравнение Прандтля основано на предположении о наличии резкой границы раздела между турбулентным ядром и ламинарным sub-layer.
Процесс развивающего обучения Турбулентность до сих пор была установлена Между этими зонами имеются прослойки, в которых обмен молекулами и молями должен быть одинакового порядка эффектов. Исходя из этого, карман впервые вывел уравнение турбулентного теплообмена и экстраполировал результаты измерения скорости, принадлежащие Ннкурадзе, на wall. In точно так же Вышеупомянутые работы Маттиоли 1940 и Гофмана 1940 предполагают существование полуслойного слоя, как это предусмотрено в работах Белтера и его сотрудников 3. Позднее эта теория была дополнена Рейхардтом, который специально четко сформулировал гипотезу, вытекающую из ценностного уровня знания.
Пустое пространство может по нашему усмотрению иметь форму сферы, и мы подсчитаем плотность излучения в центре этой сферы. Людмила Фирмаль
Следующие выводы являются смежными экений Рейхардт. В уравнениях 124 и 125 мы выбираем молекулярный показатель напряжения m и показатель турбулентности T Из уравнения. Где Pr Pr Pr D M-обобщенное число Прантля, введенное Рейхардтом, а AQ a соответствует нормальному числу Прантля только в некоторых cases. So … Числовой Pr не является чисто физической константой, такой как Pr. Это может варьироваться в зависимости от характера потока, а также Точка потока. Введение числа Pr означает, что не делается никаких предположений относительно сравнительных значений коэффициента турбулентного обмена Aq и 4, и поэтому Прандр исчезает. Поэтому индекс турбулентного обмена не должен быть на стене.
Используя уравнения, можно вывести зависимость между полем температуры и полем скорости. Ввести безразмерные координаты в обоих полях Где doo и IV указывают максимальное значение оси Y для трубы, а для плоской пластины-значение вне пограничного слоя. Для уравнений температуры. Отдельно получаем от Если сравнивать оба уравнения, то желательно Поэтому ради скорости Физические константы уравнения 145 считаются постоянными. Интеграл в уравнении 145 позволяет найти значение заданного поля скоростей, p y d К d ld ylr.
Уравнение для p 1, 145, должно быть 1.Число нуссельта можно определить Кроме того, значение H 1-0w 0a-w вводится таким образом, что коэффициент теплопередачи обусловлен средней разностью температур. Для закрепления уравнения 145 на основе только общих представлений о свойствах турбулентного течения необходимо несколько специальных допущений. Решите следующее уравнение 149 a. обобщенное число Прандтля Pr Pr Av A. предпосылка классической теории A, A, была впервые поколеблена Фейджем и Фолкнером 1 в аэродинамическом следе нагретого цилиндра АФ а, есть 1. Позже D 4, 2 были получены экспериментально со свободными flow.
Эксперимент Элиаса 1, широкое согласие характеристик температурного и скоростного полей Согласно Райхардту, турбулентный пограничный слой пластины обтекаем и принимается продольно потоком воздуха. Следующее описание. Отношение коэффициента турбулентности к числу 0,72 Замена должна иметь значение ДдА, 1,4.Согласно уравнению 145, значение d0 dp 1 совместимо только с Рг1.И так оно и есть. Эффекты трения по сравнению с AJA меньше, чем в свободном потоке, и это, безусловно, объясняется воздействием стены. Ad A.
Расстояние от Ad1A непосредственно до стенки 1 увеличивается, и значение, по-видимому, увеличивается до 2.So, среднее значение Ah A равно Расчет по формуле 145 должен быть между обоими этими значениями. Однако среднее значение ДдД и Ш этого типа может также зависеть от самого числа Прандтля PR2.3 99, максимальный градиент при высоком числе Прандтля Температура возникает около стены, где Ад а приближается к значению 1.So вы получаете предельное значение. Среднее значение отклоняется от этого сильно ограничить и число Прандтля уменьшается. Впрочем, даже в пр-0 Свободные струи. Я предварительно установил DD 4 в 1.3, потому что в настоящее время нет более точных данных. B.
Коэффициент коэффициента трения A, c. In в классической теории предполагалось, что в ламинарном пограничном слое коэффициенты турбулентного обмена равны D, 0, а в ядре потока-t 0.С Между тем, из уравнения 141, чем выше число Pr даже если значение С1 ТТ очень маленькая, с большой турбулентного переноса тепла можно. Рисунок 1 99, этот эффект находится в области более высоких температур Градиенты у стенок, зоны с большим количеством пр, даже слабые пульсирующие движения могут вызвать интенсивный теплообмен.
Поэтому теоретический результат очень велик Степень принятого закона изменения функции расстояния l, A, m, установление этого закона осложняется тем, что изменение функции A, q, оказывающее большое влияние на теплообмен, очень велико Это немного влияет на поле скорости, которое является единственным доступным измерением. Рейхардт принимает приближенную форму A, t, а коэффициент турбулентности a равен Максимальное значение площади полной турбулентности непрерывно уменьшается до нуля по мере приближения к стенке.
Значения, найденные Райхардтом, приведены в таблице.16 в зависимости от безразмерного расстояния от стены когда y равно 6, L можно вставить.12.7 10-5 г 6 Вместо того, чтобы разделить турбулентность на 2 части по Прандтлю или 3 части по Кальману, Рейхардт больше не делает четкой зоны division. As в крайнем случае он Предлагается ввести понятие некоторой преобладающей вязкости. Этот слой начинается примерно с 11. Это зависит от стены. Но незначительные Таблица 16 Отношение коэффициента турбулентного трения A к вязкому ij в зависимости от безразмерного расстояния от стенки Рейхардт. c.
- Отношение теплового потока к импульсному потоку общая формула 145 из b становится возможной, если сделать еще одно предположение о величине. Постоянный поток в трубе, касательная Напряжения, рассматриваемые индивидуально, изменяются в соответствии с законом M1-y G. Это связано с тем, что M0 также должен присутствовать по duldy Q на оси трубы. На стене, Т tte1 и Q кя Ил. Поэтому мы можем положить Где k меньше 1 и равно нулю.
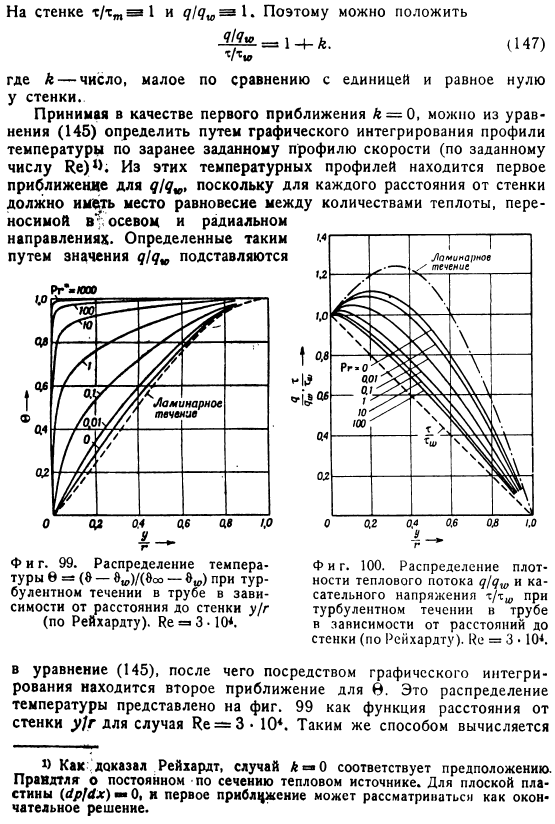
В качестве первого приближения уравнение 145 может быть определено графическим интегрированием профиля температуры в соответствии со следующим заданным профилем скорости Из этих профилей температуры, количество 1 дан Найдено второе приближение O, распределение температуры показано на фиг. Расстояние от стенки в случае Re 3-104 99 в зависимости от y r. Он рассчитан 1 Как доказал Рейхардт, случай 4 0 соответствует предположению. Прандтль о постоянном источнике тепла поперечного сечения. Для плоской пластины dpjdx равен 0, и первое приближение равно Это считается окном. Распределение температуры соответствует параболическому распределению скорости ламинарного потока в трубе.
Для этого предварительно необходимо установить связь между плотностью излучения иь и интенсивностью излучения 1ъ полости с небольшим отверстием, стенки которой находятся при постоянной температуре. Людмила Фирмаль
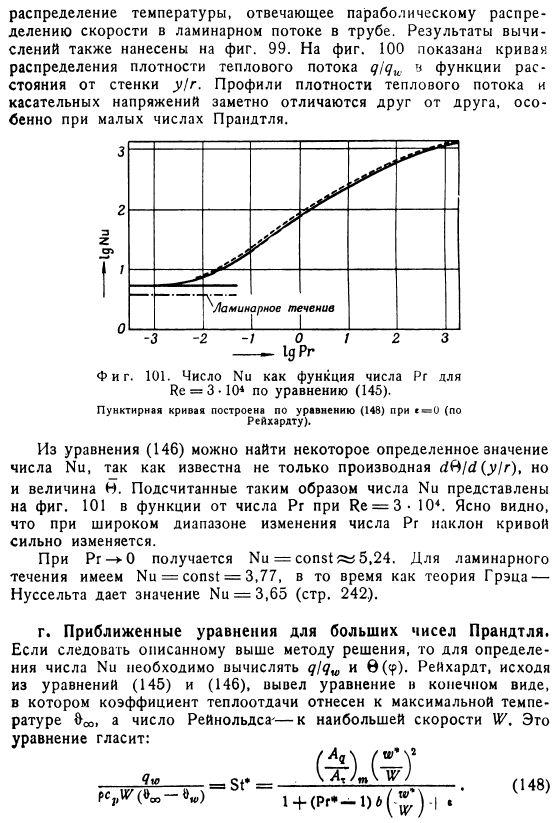
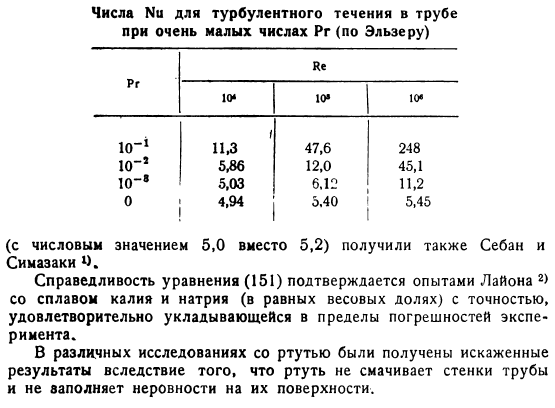
Результаты расчетов также представлены на рисунке. На рисунке 99 100 показана кривая Распределение плотности теплового потока q qw в зависимости от расстояния y r от стенки. Профиль плотности теплового потока и Из Формулы 146 мы можем найти постоянное значение числового Nu, поскольку нам известна не только производная dft d y r, но и значение B. числовое Nu вычисляется таким образом Рис. 1 Re 3-101 как функция числового Pr в 10.It понятно, что наклон кривой сильно меняется из-за широкого варьирования числа Pr. Для Pr-0, Nu const r 5.24 является obtained. As для ламинарного течения существует nu const 3.77, но в теории Граца-Нуссельта значение Nu 3.65 p. вы получаете 242. D.
Приближенное уравнение большого Прандтля number. To определив численное значение Nu, нужно вычислить qjqw и 0 p, если следовать приведенному выше решению. Лайкерт прэдинг Из уравнений 145 и 146 он вывел уравнение в его окончательном виде. Коэффициент теплопередачи связан с максимальной температурой Oco, а число Рейнольдса-с максимальной скоростью UZ. Это уравнение Переход к значению IV удобен в том смысле, что одно и то же уравнение может быть использовано для продольно обтекаемых пластин с учетом их индивидуальных характеристик. Оба тока. Связь между уравнением 148 и prpr 134, то есть если поставить Pr, используя отношение C 8 w lV 2. Но…
В то же время обнаруживается принципиальная разница. Поправочный член e содержит значение k в уравнении 147. Для плоской пластины можно установить значение e 0.Это дает конкретное приближенное решение течения в трубе. Но важнее другое Значение b в уравнении 148.Это значение можно рассматривать как меру толщины ABb cf или, соответственно, A, t 1 IPt и, следовательно, молекулярного слоя. Теплопроводность преобладает над турбулентным обменом. Согласно классической теории, толщина слоя определялась как величина, не зависящая от числа Прандтля. W w в уравнении 134 были чисто гидродинамическими свойствами. По данным Рейхардт, есть слой доминирующим доминирующим вязкости и теплопроводности.
Молекулярный обмен является доминирующим. Переход на границе слоя является непрерывным. Только в случае Pr 1 толщина обоих слоев будет совпадать. Чтобы решить формулу 148, нужно указать число b. для PrRe 2 500 значение b. Как показал Рейхардт, оно зависит только от Pr. В качестве приближенного выражения 1 РГ 200 принимается Это уравнение хорошо согласуется с полуэмпирическим уравнением, предложенным Тен-Бошем1. Для Re 3-10 Nu числа, найденные из Формулы 148, также строятся. Тоже фигура.
Кроме того, Е 0 равно accepted. In к тому же, в преобразовании к скорости, голова температуры 8-8. — Заметьте, transl. It действует как личность. Отклонение незначительное. Nu, полученный в Формуле 145 Важность теории Рейхардта заключается не столько в ее методах, сколько в получении результатов, которые немедленно используются на практике. На основе наиболее распространенных предположений о турбулентности В обмене, представленном формулами 139 и 140, создается формула распределения температуры 145.Только при интегрировании в это уравнение будут введены предварительные условия В отношении специфических свойств личности expressions.
Кроме того, первостепенное значение имеет Формула 4, с помощью которой происходит процесс постепенного затухания турбулентного потока. При приближении к стене рябит. e. передача тепла при очень малом Прандтле number. As это видно из рисунка. 99, очень небольшое количество Pr, основная часть температурного напора попадает в турбулентную область. Процесс в непосредственной близости от стены уже не является решающим. Таким образом, температурное поле приобретает ламинарные характеристики. Турбулентность от стенок, молекулярная теплопроводность предпочтительнее молярного обмена или, по крайней мере, того же порядка величины.
Х-бу, соответственно Pr-0, численное значение Nu зависит только от поля скорости, то есть от численного значения Re. Рейхардт, путем расчета по формуле 145, в данном случае получил значения, указанные в таблице. 17. Таблица Р Пр-н ну Рейхардт Используя тот же метод В предположении Рейхардта о распределении скорости вблизи стены Эльзер получил близкое значение таблицы. 18, точно соответствует значению Pr 0 Рейхардт. Для этих значений Elser предлагает приближенное выражение с ошибкой 5 или меньше Как и прежде, ему присваивается среднее значение температуры и скорости.
Полностью аналогичные уравнения По словам Эльзера, несметное количество турбулентности в трубе в очень малом количестве пр Вместо 5.2 мы получили номер 5.0, Северн и Симадзаки О. Справедливость уравнения 151 была подтверждена экспериментом Лиона 2 с сплавом калия и натрия в той же массовой доле с точностью, которая хорошо вписывается в диапазон погрешностей. Эксперимент.
Смотрите также:

