Оглавление:







Метод тепловых источников Прандтля
- Для Pr 1 простое выражение 128 больше не является допустимым. Это видно по следующим причинам на достаточном расстоянии от стенки коэффициенты турбулентного обмена A и Aq равны. Числитель константы Q и X являются отличными, и даже в PR 1, если только предварительно предполагается, IAntataconst, они пропорциональны между 9 и Вт напротив, у стенки должен быть слой, в котором турбулентный обмен ослаблен и молекулярная миграция имеет первостепенное значение. Но при этих условиях слой граничного слоя P. As уже установленное в 258 году сходство между обоими полями сохраняется только в Pr 1.
Однако процесс, который происходит в слоях, близких к этим стенкам, имеет важное значение для определения теплопередачи. Поэтому, чтобы получить одновременный Пропорционально скорости и температуре основного потока и околоземного слоя Прандтль разбил турбулентность на 2 части zones. In турбулентное ядро, преобладает турбулентность. Так, в этой зоне вязкость и теплопроводность полностью возвращаются к background. In Граничная зона ламинарного подслоя 4, она равна нулю, поэтому здесь возможен теплообмен Это делается только для теплопроводности и передачи импульса-только для вязкости.
Последующая часть этой главы посвящена выведению законов излучения абсолютно черного тела. Людмила Фирмаль
Прантл не из уравнений 124 и 125, а из дифференциальных уравнений 10 г движения и 17 г энергии Уравнение энергии 130 вводит интенсивность теплового источника d. это соответствует термину gradp в уравнениях движения. В условиях стабильного течения профиль скорости сохраняется, так как градиент давления, необходимый для течения в трубе, компенсирует импульс, приданный стенке. Это не так change. In в отличие от этого, если количество тепла, обмениваемого со стенкой, не восполняется, температура жидкости будет ближе к температуре стенки По его притоку или ответвлению. Поэтому выход источника тепла q определяется непосредственно из условия, что температурный профиль не изменяется.
Как это кстати, можно добиться желаемой пропорциональности между B и w. при выводе уравнений 127 и 126 эта аналогия посылается заранее. Поэтому эти уравнения строго справедливы. Только для обтекания пластины град 0. На самом деле источника тепла q не существует. Поэтому введем вымышленный источник q. он должен быть постоянным по поперечному сечению, как и град p, и фактическим Температурное поле. Но температурный профиль турбулентного потока уже полностью выровнен, поэтому ожидается лишь небольшое отклонение и будет более ориентированным Более высокий коэффициент теплопередачи обусловлен более сильным нагревом пограничного слоя 2. Внутренняя часть слоистого подслоя толщиной е фиг.
97 Видов должны линейно возрастать до величины B, и из этого, из равновесного состояния силы, получается следующее соотношение Здесь принимается R-s asr. Тепла на единицу длины трубы передается через ламинарный пограничный слой Для турбулентного ядра, согласно предположению, дифференциальное уравнение 129 и Подставляя значение коэффициента k и соотнося выход источника тепла с единицей длины трубы, можно увидеть Уравнения 132 и 133 можно считать эквивалентными друг другу, так как это количество тепла должно проходить через ламинарный подслой.
- Если вы сравните их, вы получите отношения Если количество неизвестно О В то же время, подставляя это уравнение в уравнение 132, мы вводим коэффициент теплопередачи e Q B2nr. Вместо разности Вводя давление, коэффициент сопротивления определяется уравнением Р Кроме того, постройте число Nu a2r k, число Re u 2rp i Hp w w и, наконец, Уравнение Прандтля. Сто тридцать четыре Для Pr I уравнение 134 является уравнением 128.Коэффициент сопротивления обоих уравнений может быть определен законом Блазиуса 2, установленным экспериментально.
Турбулентность в гладкой трубе Формула 135 справедлива для значений от 2300 до 80 000 Re, и поэтому охватывает значительную часть всех случаев, которые действительно важны для этой методики. Здесь числитель формулы 134 определяется как Заметим, что сходство сопротивления и теплопередачи справедливо только в случае чисто фрикционного сопротивления. Для достаточно грубых узелков Сопротивление формы потока начинает играть заметную роль, уравнения, построенные по простой аналогии, теряют свою интенсивность 3 В уравнении 134 фактор p w w все еще неизвестен. Поверхностная скорость ламинарного подслоя может быть четко определена на основе известного распределения скоростей.
Уменьшая отверстие, можно воспроизвести свойства абсолютно черного тела с желаемой точностью. Людмила Фирмаль
В случае турбулентности, например, по степенному закону с показателем Возникает из закона сопротивления брасиуса, где y-расстояние от стены, Wmso. — Скорость на оси трубы таким образом, Prandtl4 Наклон-к-сопротивлению Таким образом, формула 134 принимает вид Уравнение Прандтля было вторично получено Тейлором 1.Эти. Уравнения очень важны для дальнейшего развития теории теплопередачи. Позже было установлено, что чем выше значение числа Прандтля, тем больше формула становится слишком большой, поэтому появился ряд работ, посвященных совершенствованию уравнений 134 и 136. Неточный.
Были внесены улучшения, в основном связанные с функцией yes w, но в большинстве случаев общая форма уравнения 134 не изменилась changed. In сложение, вместо р Re также использовался в Re, Pr 2.Функции, используемые в некоторых случаях, очень сложны и имеют в результате полуэмпирическое происхождение Сравнение с экспериментальными данными теоретически обосновано более детальным исследованием обменных явлений между турбулентным ядром и ламинарным подслоем. Уходи Помимо вопроса о полноте круга проблем, назовем еще одного автора. Их исследования примыкают к этой области. Гофман 7, Карман6, Маттиоли, Рибо 1.Среди работ, имеющих характер рецензирования, назовем статьи Эккерт11 и Коч12.
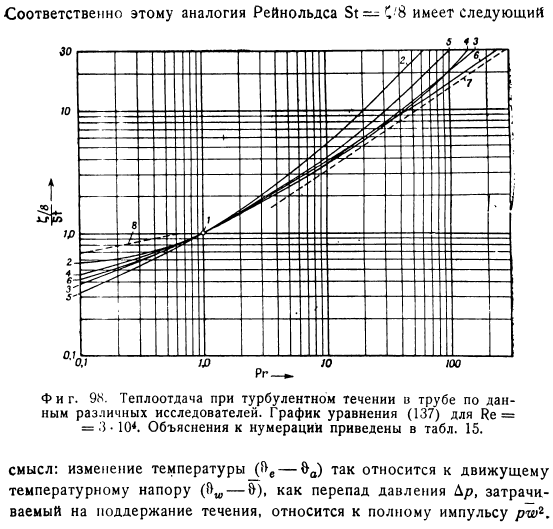
Большинство уравнений, принадлежащих этим авторам, являются St C 8 Re, Pr. Обратное выражение Таблицы, представленные некоторыми из упомянутых исследователей, обобщены в таблице. Соответствующие значения показаны на рисунке delagrow. 98, Re 3 в 10. Уравнение турбулентного теплообмена Таблица 15 Формат Nu Pr, например уравнение 173 Направление, связанное с применением функции опыта в виде Nu Pr0, например формулы 151 Функция опыта График показывает, что по крайней мере до Pr 50 кривые 3-5 очень близки друг к другу. Даже если значение числового PR-это большой, уникальный Зависимость, поскольку сильные флуктуации физических констант приводят к большим вариациям экспериментальных данных. См.
Если величина Pr очень мала, то предложенное уравнение имеет вид Другие предварительные условия, которые необходимо принять, см. на стр. 299.Рис. 1 98, плюс 2 линии, определяющие наклон кривой. Это соответствует эмпирической зависимости, которую мы будем рассматривать later. In в любом случае, мы видим, что чем шире диапазон значений Pr, тем больше наклон кривой. Значение Sf t 8 можно легко представить как значение которое можно измерить сразу.
Смотрите также:

