Оглавление:






Температурное поле зависит от двух координат (плоское двумерное стационарное температурное поле)
- Вводный раздел (стр. 15 и далее), я был знаком с областью 3 принципиально важных физических величин. Эти поля являются: 1) скалярное температурное поле. 2) векторное поле градиента температуры 3) векторное поле теплового потока. Дальнейшие исследования будут зависеть от соображений данного раздела. Рассмотрим только случай плоского температурного поля. Это означает, что предполагается распределение. Температура всех плоскостей, параллельных плоскости чертежа, одинакова. Другое layers.
Предполагается, что распределение температуры происходит только от 2 координат г 57 изображен в состоянии проникновения теплового потока. Поверхность 1 поддерживает постоянную температуру, а поверхность 2 поддерживает температуру 1>2.Следовательно, обе поверхности Он представляет собой плоскую поверхность и дает изотермы при пересечении со строительной плоскостью. Рис. 1. также показаны несколько промежуточных Изотерм. Давай. Поверхность, предполагая более теплую, постепенно перемещается из точки eₜ и проводит линию градиента температуры в точку eₜ.Согласно ранее принятому В терминологии эту линию можно также назвать линией теплового тока. Нарисуйте 2-ю такую линию от точки.
Эта разность, однако, мала по сравнению с разностью давлений, определенной уравнением (12-14), до тех пор, пока давление испарения не приближается близко к критическому давлению кипящей жидкости. Людмила Фирмаль
Стеновая поверхностная полоса. Между этими 2 линиями eee₂ и fₜf₂, она вызвана трубкой теплового потока. Совокупность всех Изотерм и всех линий теплового потока образуют сетку кривых, дающих изображение Распределение температуры и теплового потока. Эта цифра становится еще более очевидной, когда вы устанавливаете тот же температурный интервал₍DO, а затем выбираете точку e / D. g,. Так что одинаковое количество тепла соответствует всем тепловым потокам pipes. In в этом случае сетка имеет свойства для всех ячеек во всем пространстве В температурном поле вы получаете постоянное соотношение сторон.
Для доказательства получим одну из ячеек и как отрезок на изотерме, показанный Dn в отрезке на линии. Температурный градиент. Затем, для количества тепла, проходящего через D$; получаем формулу Эта формула должна содержать одно и то же значение для всех участков конкретной токовой трубки и всех токовых трубок в поле под consideration. In кроме того, значения X и D8 являются、 Постоянное значение. Таким образом, отношение D $ ’ Ду должно быть постоянное значение, если это необходимо. Определите количество теплоты, получаемой через определенную часть поверхности тела, например, а^. нулевая линия-это линия теплового тока через A.
Вплоть до линии теплового тока. Проходит общее количество тепла Вы можете. Очевидно, что он отображает определенное значение для Qₑ. Как уже упоминалось выше、 В этом разделе мы рассмотрим только 1 из приложений общей теории потенциала. Для дальнейшего анализа рекомендуется использовать сходство с тем, что рассмотрено ниже Механика жидкости (то есть потенциал и соленоиды) полем без вихря и источника. Потенциал скорости (обычно обозначаемый Φ или p) соответствует температуре 8. д.58. 57.Или W) соответствует текущему, стр. 18. Функция тока (обычно F и mine обозначаются через P или f) соответствует функции теплового тока Q.
Скорость (обычно обозначается v как тепловой поток q (т. е. Рисунок 1: на рисунке 58 показано крупномасштабное воспроизведение одной из 58 секций, показанных на рисунке 1. 57, на чертеже направления осей x и y являются fixed. In кроме того, построены 2 линии теплового тока Q. Базовый треугольник, включающий Q-f-dQ и ногу dx, dy. Тепло dQ входит в этот треугольник со стороны dx. Такое же количество тепла будет стекать с бокового штампа. Так…
- Если вы разделите первое уравнение на dx и разделите второе уравнение на dy и измените порядок. Дифференцируя первое уравнение относительно x, дифференцируя первое уравнение относительно x, дифференцируя 2-е уравнение относительно x, получаем 4 из следующего: Из выражений (e) и (e) обе скалярные функции & = / » ( * .Y) и Q = fq (x, y) должны удовлетворять дифференциальному уравнению Лапласа. Уравнения (g) и (a) характеризуют свойства векторного поля теплового потока. От Уравнение (h) означает, что магнитное поле не содержит вихря(потенциала), а согласно уравнению (g), нет источника (то есть это соленоид).
Изометрическое отображение Комплексная переменная Z = X — * — Y, определенная в комплексной плоскости (Z-плоскость), имеет вид、 Возведение в степень другой комплексной плоской функции отображения F (z = x — +(y). в этом случае уравнение выглядит следующим образом: z = F. (Z) или x — + / y = T (X — + / T)=Φ (X, T)+ T(X, T))、 Кроме того, в последнем выражении комплексная величина F (X + lY}разлагается на части действительного Φ и мнимого IV. В сущности, конформное отображение основано на предположении, что функция отображения является аналитической функцией. Это функция Φ и V удовлетворяет условию Коши-Римана.
Термодинамика показывает, что давление насыщенного пара, находящегося в равновесии с жидкостью при определенной температуре, разделенных плоской поверхностью больше, чем давление насыщения на кривой вогнутой поверхности. Людмила Фирмаль
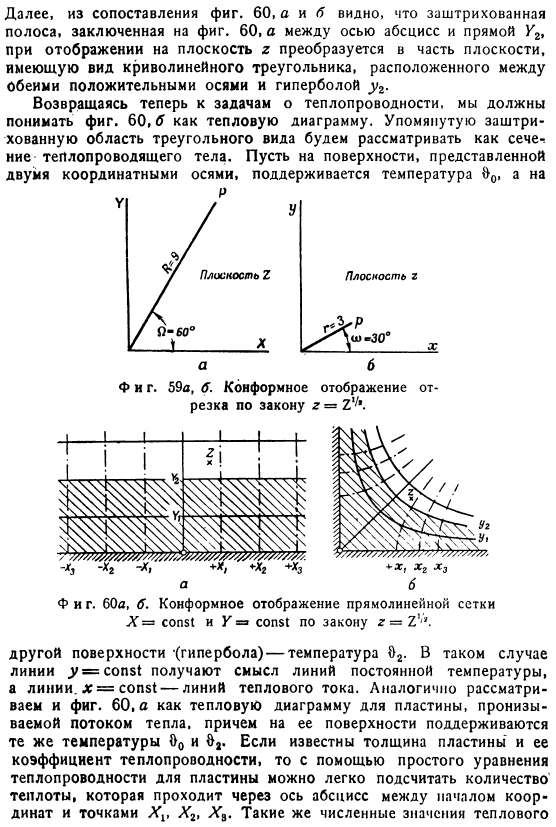
Следовательно, дифференциальное соотношение Коши-Римана Он заполнен с Это аналитика. Особенности. Ниже мы рассмотрим функцию отображения z =Z⁴ ’с чисто математической точки зрения. Это, как вы знаете, аналитическая функция. Сделайте оба комплексных числа каноническими: 。 вместо Z =Z⁴ 2 комплексные числа равны только друг другу Мнимые части будут равны по отдельности. В таком случае, следовательно Когда действует 。 Точки P, определенные в плоскости Z двумя координатами R = 9 и 2 = 60°, определяются как точки с координатами r = 3 и w = 30°(рис.59, А и в). Рисунок 1 на рисунке 60а показана Z-плоскость пересекающихся линий X = const и Y = const.
Перенесите отдельные пересечения этой сетки на плоскость z, используя отношение r Для = R R и w = 1/, 2 семейство из 2 ортогональных линий передается в семейство из 2 ортогональных биссектрисных гипербол(рис. 60, б). Кроме того, рис, а при отображении в z-плоскости между абсциссой и прямой Ug она преобразуется в деталь Плоскость в виде изогнутого треугольника, расположенная между положительной осью и гиперболой Y. Здесь мы должны вернуться к проблеме теплопроводности и понять рисунок 1.60, b как рисунок горячей проволоки. Заштрихованные области вышеупомянутых треугольников рассматриваются следующим образом: Сечение проводника тепла.
Координатных оси для поддержания температуры 9°на поверхности、 б Тоже фигура. 59а, 6.Конформное отображение интервала по закону r = Z’a. Тоже фигура. 60A, b. конформное отображение линейной сетки X = const и Y = const согласно закону z =Z1*. Другая поверхность (гиперболическая) — температура 0.In в этом случае линия y = const получает значение линии с постоянной температурой и линией. x = const-линия термической Current. In точно так же Рассмотреть и понять.
Однако в качестве тепловой диаграммы пластины, пронизанной тепловым потоком, на ее поверхности поддерживаются те же температуры% и 8а. Если толщина известна Вы можете легко вычислить это число, используя теплопроводность пластины и простое тепловое уравнение пластины Тепло, проходящее по горизонтальной оси между началом координат и точкой Xₜ, X₂, Xₛ.Такое же количество тепла Поток также действителен для участка абсциссы между началом координат и точкой. 60 б Этот простой пример показывает читателю только связь между теорией теплопроводности и методом конформного отображения.*> Дополнительную информацию по этому вопросу см. В книгах рота, Олендорф и Полхаузен.
Смотрите также:
| Метод электрической аналогии | Проникновение тепла в односторонне ограниченное тело через площадку круглого сечения |
| Стационарное температурное поле без источников тепла | Понятие о тепловом сопротивлении |

