Оглавление:




Комбинированные краевые задачи
- Во всех рассмотренных выше задачах временные и пространственные граничные условия были заданы в такой простой форме, что было установлено, что они были бы возможны при одном и том же решении дифференциального уравнения. Уравнение удовлетворяет одновременно всем требованиям, содержащимся в граничных условиях. Если такого рода корректировка граничных условий и решение не представляется возможным ни для одной из задач, то совокупность требований, содержащихся в граничных условиях, должна быть разделена на группы Частичные требования. Затем для каждой такой группы находят соответствующее решение дифференциального уравнения.
Предположим, что такое частное решение является функцией Также ясно, что сумма 0 = u4-V 4-IV- | — представляет собой решение дифференциального уравнения теплопроводности. Это потому, что это линейный дифференциал. Equation. In в этом случае, если корректно выполняется только разложение на частичные требования, то удовлетворяются и требования, выраженные в граничных условиях. Подобный этому Возможность решения поставленной задачи во многом зависит от правильного выделения требований, содержащихся в граничных условиях. Первый пример.
На этом рисунке значения критерия Рейнольдса пленки конденсата нанесены как функция значений безразмерной величины критерий Прандтля рассматривается как параметр. Людмила Фирмаль
Предположим, что задача о пластине, которую мы уже рассматривали в качестве введения, решается при следующих условиях: Как и прежде, предположим, что для распределения времени I = 0 начальное распределение d = f (x) равно given. In кроме того, температура обеих поверхностей претерпевает изменения во времени, она может Быть как периодическим, так и непериодическим. предположим, что x = — ± — X имеет k = (( / ), а X-± — X имеет 0 =φ ()). В этом случае граничные условия можно классифицировать следующим образом: (вешалка. И): таблица и Очевидно, что решения$ =и V4-одновременно удовлетворяют всему набору граничных условий. 2-й пример.
- Задача 6 получила дальнейшее развитие в этом примере, посвященном колебаниям температуры(стр. 110). Таким образом, температура момента времени/ = 0 равна Величина всего объема тела равна нулю. Только после этого на поверхности тела возникают колебания температуры. Разбейте искомую функцию$на 2 конкретных решения u и y. следуя решению задачи 6, рассмотрим распределение температуры, которое периодически изменяется в виде уравнения(42).В зависимости от принятого решения В этой задаче мы предполагали, что колебания будут происходить в течение длительного времени, когда первое распределение уже не будет играть роли. Мы могли бы получить уравнение.
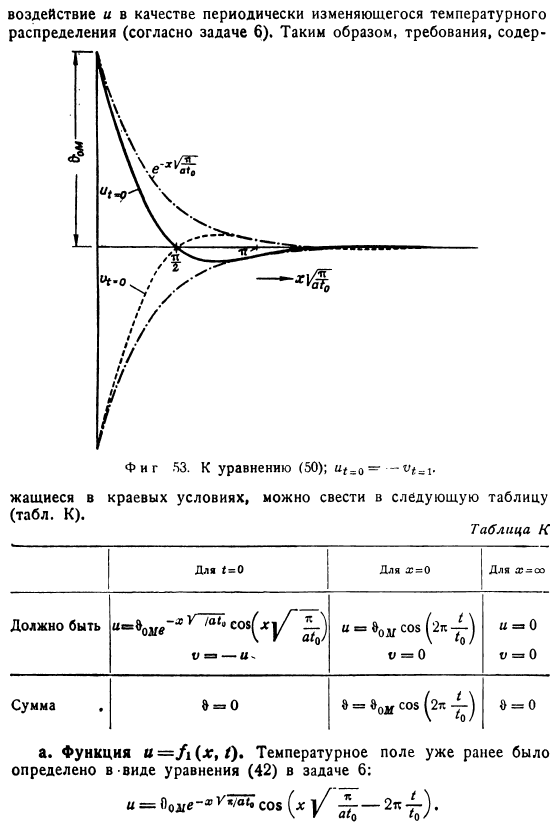
Если вы также исходите из первоначального распределения Эта формула соответствует формуле для i = 0 (42) (рис. 53). Он накладывает периодически меняющуюся функцию температуры и функцию температуры распада, y, и требует, чтобы функция была дополнена до нуля с моментом времени/ = = 0. Таким образом, кривая^ = 0 должна быть зеркальным отражением кривой » G0 относительно линии нулевой температуры (см. рис. 53).
Результаты расчетов показывают, что для турбулентной пленки конденсата критерий Нуссельта является функцией безразмерной величины, уравнения (12-9) и критерия Прандтля для конденсата. Людмила Фирмаль
В начале процесса, то есть до тех пор, пока это почти полностью подавляет равномерное изменение распределения температуры и, пока начальное распределение y все еще в целом сохраняется. Но со временем、 затухание распределения y имеет меньшую величину и effect. In в соответствии с ним, в чистой степени, эффект проявляется в чистой форме, периодически Изменение распределения температуры(согласно заданию 6).Таким образом, требования включают в себя: Рисунок 53.To формула (50).И^ _0 = — VI -! Жизнь в граничных условиях суммируется в следующей таблице (Таблица K). Таблица К A.
Смотрите также:
| Периодически изменяющаяся температура | Применение метода конечных разностей |
| Тело, ограниченное с одной стороны (полуограниченное пространство) | Метод электрической аналогии |

