Оглавление:







Тело, ограниченное с одной стороны (полуограниченное пространство)
- Температура поверхности полуограниченных объектов под воздействием внешних воздействий периодически колеблется в районе нуля. Давайте изменим температуру. Если это происходит в соответствии с законами гармонических колебаний, то необходимо определить величину теплового потока через поверхность как по типу температурного поля, так и по временной функции. a. тип температурного поля. Выражение если φ (X) является решением уравнения, то частичный Интеграл теплового уравнения. Это решение является уравнением F(х) = Се Так что если это 0, вы получите выражение Использование формул. Преобразует это выражение в форму 8 = Се * / соѕ(?Гц ЗТ ц). Полученное комплексное решение можно разделить.
Реальное и воображаемое parts. As в результате находим 8 = 0,+ — / 0r. Обратите внимание на следующее: Согласно свойствам экспоненты, знак плюс экспоненты — это расстояние от поверхности, а также температура Колебания всегда должны увеличиваться. Этот результат явно не согласуется с опытом. Поэтому, по физическим причинам, во всех случаях верхний знак может быть удален. После этого останется 2 решения Чтобы определить любые константы C и q, установите x = 0 в обоих уравнениях, используя условия поверхности. Oo =Coscos (tfat) или 0ₒ=C₂sin(?2а). Сравните эти формулы с условиями поверхности[стр.
Перенос тепла через турбулентную пленку конденсата можно рассчитывать методами, относящимися к турбулентному потоку жидкостей или газов вдоль плиты. Людмила Фирмаль
Принимать форму Затем уравнение температуры При обсуждении результатов… Личная перспектива. Во-первых, вы можете исправить конкретную проблему В какой-то момент изучите форму температурного поля в этом месте. moment. In другими словами, вы можете получить мгновенное изображение распределения температуры. Во-вторых, вы можете рассмотреть создайте бесконечно тонкий слой на глубине x и исследуйте изменение во времени температуры, которой подвергается этот слой. Сначала учтите первый метод и начните с самой простой функции Эта зависимость является волновым уравнением, выраженным в косинусных волнах.
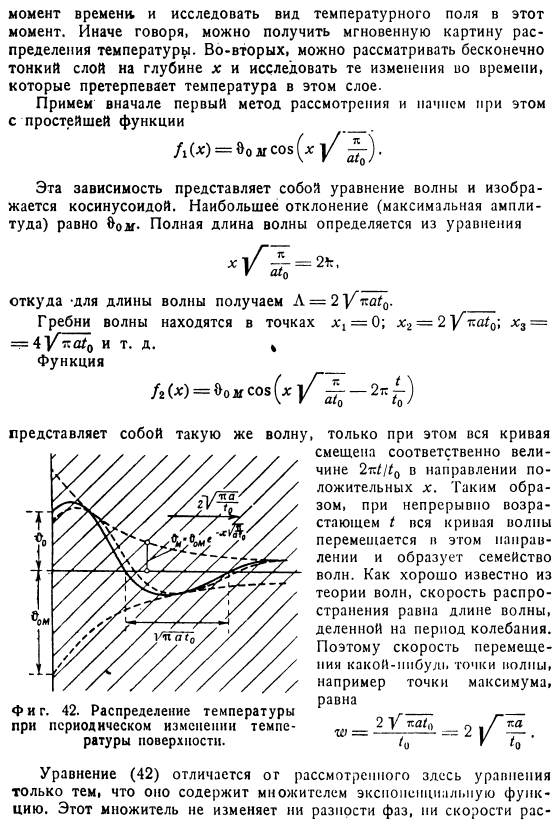
Максимальное отклонение (максимальная амплитуда) равно спецификации, общая длина волны равна Уравнение Для длины волны используется fnat₀ [A = 2]. Гребень волны находится в точке*,= 0. xg = 2 Vco /₀; xₛ= 4 / etc etc Представляет одну и ту же волну. Только в этом случае вся кривая смещается на 2irf /t₀ в направлении положительного x соответственно. Поэтому, непрерывно увеличивая I Вся кривая волны движется таким образом, образуя family.
Хорошо известно из волновой теории, что скорость распространения равна длине волны, деленной на период колебаний. Следовательно, скорость Пример: Макс Тоже фигура. 42.Распределение температуры с периодическими изменениями температуры поверхности. Формула (42) отличается от рассматриваемой здесь Формулы только тем, что содержит коэффициент экспоненциальной функции. Этот фактор также не изменяет разность фаз Скорость Он не находится ни в пространстве, ни в длине волны, но с увеличением x максимальное отклонение уменьшается очень быстро. На рис. 1, рис. 42 показана кривая температуры в 2 смежных точках. Тоже фигура.
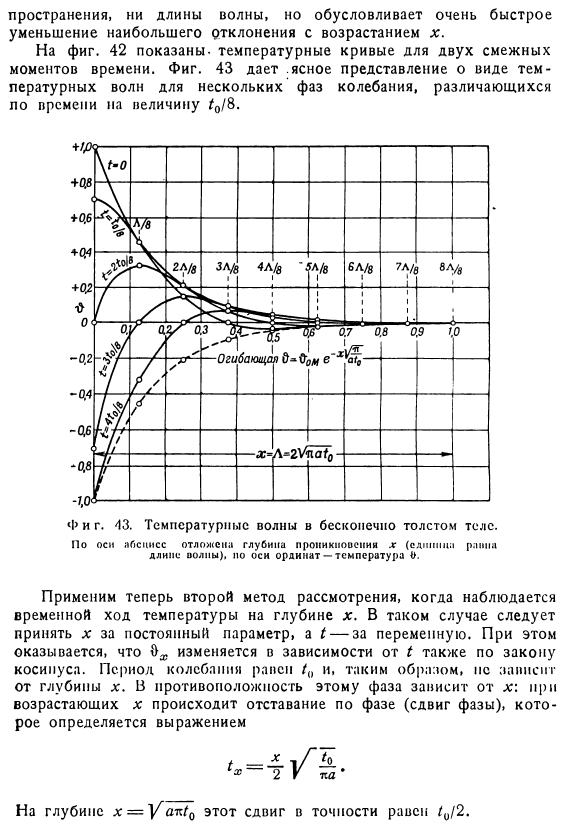
Дает четкое представление о форме температурной волны в некоторых фазах вибрации. t₀ / только 8 отличаются по времени. F и G. 43.Температурная волна бесконечно Толстого объекта. Если временной ход температуры наблюдается на глубине x, примените 2-е соображение method. In в этом случае x должен использоваться как постоянный параметр, а t-как переменная. 9 ^показывает, что она изменяется с t в соответствии с законом Косинуса, который зависит от T. Так как период колебаний равен ln, то ns зависит от глубины x. By контраст Фаза зависит от x; увеличение x имеет фазовую задержку (фазовый сдвиг), которая определяется уравнением При глубине x =Vak1₁> этот сдвиг точно равен 1″ / 2.
Максимальная амплитуда также изменяется следующим образом Здесь можно поставить вопрос: на какой глубине флуктуация температуры уменьшается до V-ой доли ее величины на поверхности? Чтобы ответить на этот вопрос, нужно решить уравнение относительно х. И далее… Ввод длины волны Л= 2]Лка / in вместо сегмента vat₀₀、 2 В П В-2 ″ Легко видеть, что чем больше длина волны (и глубина проникновения температурной волны), тем больше коэффициент теплопроводности и тем медленнее скорость. Колебания. Высокочастотные колебания просеиваются с увеличением глубины. В том, что table. In на рис.7 суммируется численное значение функции f (y).
Ход температуры земной поверхности может быть истолкован в упрощении, хорошо известном как чистая материя теплопроводности. Рассмотрим годовое изменение температуры поверхности. /₀= 1 год= 8760 часов как гармоническая вибрация в цикле. Затем берут коэффициент температуропроводности а = 0,0015 мг / час. Глубина X =Йа Sat₀= г 1,5-в 10 ″ 3×8. 76/103= 6,4 м — это 6-месячный сдвиг фазы. То есть здесь максимальная температура устанавливается на 1 месяц, а минимальная-на 7 месяцев. Амплитуда температуры Вибрация на этой глубине составляет всего 8 м / 8 м =величина на поверхности.
- В случае суточного изменения температуры поверхности(f = 24 часа) указанное явление будет в 19 раз меньше » на глубине V365. Поэтому эти вибрации будут проникать Посадка на глубину в несколько дециметров, тем более что амплитуда поверхности составляет лишь малую часть амплитуды годовых колебаний. b. поток тепла через поверхность. Определите тепловой поток с помощью первого метода (см. стр.
То есть градиент температуры поверхности После дифференцирования уравнения (42) Мы получаем Если вы консолидируете эту формулу на весь период, то получите значение, равное нулю. Поэтому вопрос должен быть представлен следующим образом: сколько стоит сумма Тепло, которое проникает через внешнюю поверхность в течение полупериода, другими словами, количество тепла, которое тело может накапливать и возвращать? Полупериодический Интеграл Таким образом, количество накопленного тепла пропорционально квадратному корню коэффициента проницаемости b и длительности 1 периода t1.
Воспользовавшись формулой Ньютона (6-2), выразим напряжение трения и, решив полученное уравнение относительно градиента скорости у поверхности стенки, получим. Людмила Фирмаль
В таблице ниже приведены значения и величины длины волны t, Qt,/ j / R6oM-0.804 / 4 для 4 различных объектов, циклические тела t которых равны 1 секунде, 1 часу и I Дню. Таблица Е Первое обобщение problem. It это более характерно. Если закон изменения не установлен на температуру окружающей среды temperature. So … Поверхностный тур Кроме того, мы предполагаем, что известен коэффициент теплопередачи a, в результате чего относительный коэффициент теплопередачи A = a / X.
Как изменяется поверхностная и внутренняя температура в таких случаях? Тело? По словам энциклопедиста. д. Математика. Wlss. V. 4, S. сто восемьдесят шесть、 (44а) Уравнение принимает вид ^)|. Сорок шесть) В этом уравнении 7), ₀ и e₀ являются величинами, которые зависят только от аргумента 1 (A2at₀).Их значения суммируются в таблице. Г.
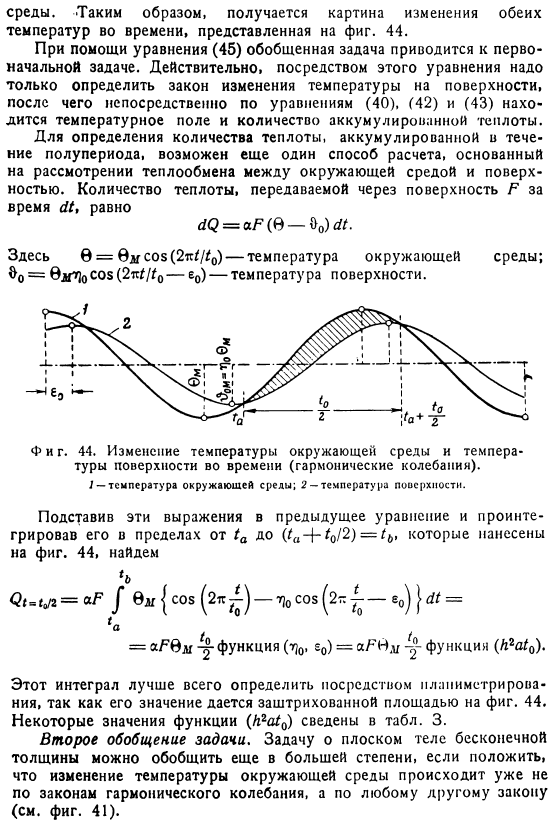
Таблица G Уравнение (446) определяет температуру поверхности 8°.То есть, если x = 0 Согласно этому уравнению, температура поверхности и температура окружающей среды вызывают гармонические колебания, причем оба колебания имеют одинаковую периодичность. Однако эти колебания отличаются друг от друга двумя способами. Во-первых, температура поверхности отстает от температуры окружающей среды на величину, определяемую ее значением. Во-вторых, амплитуда колебаний температуры В несколько раз меньше амплитуды колебаний температуры окружающей среды на поверхности Среда. Поэтому, как показано на фиг.2, получена фотография временного изменения обеих температур. 44.
Используя формулу (45), обобщенная задача сводится к начально-начальной problem. In дело в том, что по этому уравнению нужно только определить законы температуры. Тогда формула(40)、(42)、(43)зависит непосредственно от температурного поля и количества накопленного тепла. Для определения количества тепла, накопленного в течение полупериода, возможен другой метод расчета, основанный на учете теплообмена между окружающей средой и окружающей средой. Поверхность. Количество тепла, передаваемого через поверхность F в течение времени di йд = АФ (Ф> -«₀) л. Где 0 = 0m cos (2it /Z₀) — температура окружающей среды. 9₀=и и^ o cos (2 / f / 4-eo) — температура поверхности.
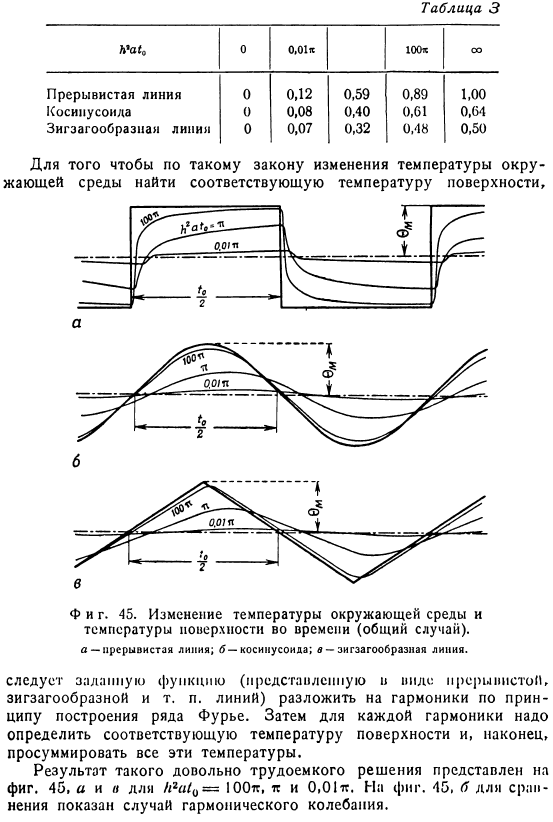
Подставляя эти формулы в предыдущее уравнение, мы интегрируем их в диапазоне от tₐ (4 + 4/2)= 4 -. 44, найти J 0M {cos (2K^) — 7oscos (2z ^ — eₒ)| / = = aR0M-ая функция (ij₀, r₀)=функция aPMm (лгц₀). Это интегральное значение показано в затененной части рисунка 4 и поэтому лучше всего определяется методом плоских измерений. 44.Несколько значений функции (h2at₀) суммируются в таблице. 3. 2-е обобщение задачи. Задача о плоских телах бесконечной толщины может быть дополнительно обобщена. Изменение температуры окружающей среды заключается в том, что оно происходит не по законам гармонических колебаний, а по другим законам(см. рис.41).
Разложить функции(в виде разложенных, прерывистых линий и т.) в гармоники по принципу Зигзаг и Ципу построения рядов Фурье. Тогда это необходимо для каждой гармоники Определите соответствующую температуру поверхности и, наконец, суммируйте все эти температуры. Результат такого довольно хлопотного решения показан на рисунке 4.In рис. 45, H * a1₀ = 100i, L и 0.Для этого есть несколько причин. 45.
Смотрите также:
| Тело, ограниченное с одной стороны (полуограниченное пространство) | Комбинированные краевые задачи |
| Периодически изменяющаяся температура | Применение метода конечных разностей |

