Оглавление:




Тело, ограниченное с одной стороны (полуограниченное пространство)
- Представьте себе, что от тела с неограниченной длиной во всех направлениях (мы рассматривали такое тело в предыдущем выпуске) отделяется половина и в области отрицательных значений X. Тогда остальная часть тела, ограниченная как внешняя поверхность плоскостью Y-2, бесконечно стирается с одной стороны этой плоскости. Такое тело называется полуограниченным space. In в этом случае задача 5 формулируется следующим образом: «температура всего полупредельного пространства в момент времени I = 0!
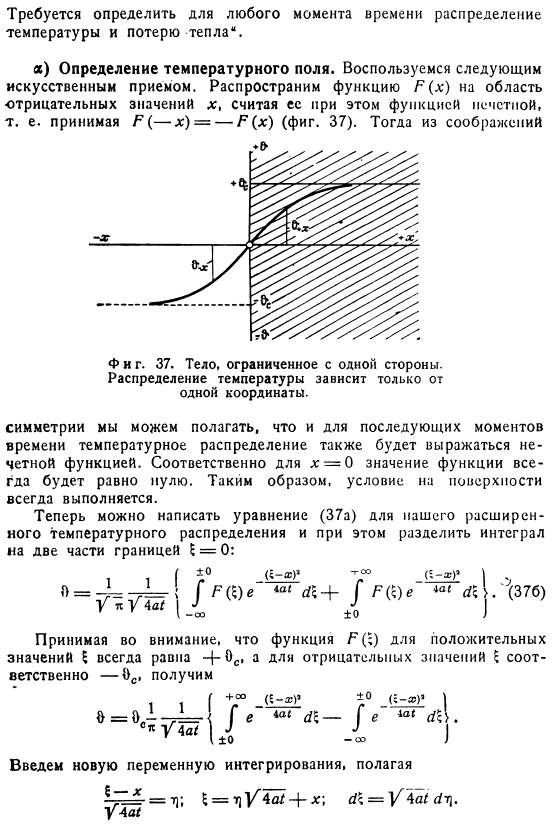
Он имеет то же значение, что и 0°.В каждый момент времени I> 0 ′ nt на его поверхности поддерживается постоянная температура на нуле Необходимо определить распределение температуры и потери тепла*в любое время. а)определение температурного поля. Используйте следующие искусственные приемы: расширьте функцию P (x) до области отрицательных значений X. Считайте это странной функцией. То есть возьмем P (- x)= — P (x) (рис.37).Тогда, по какой-то причине Тоже фигура.
Нуссельт исходил из того, что конденсат образует на поверхности стенки тонкую непрерывную пленку и что интенсивность теплового потока определяется термическим сопротивлением этой пленки. Людмила Фирмаль
Тело ограничено одной стороной. Распределение температуры зависит только от 1 координаты. В случае симметрии можно предположить, что распределение температуры также выражается в виде нечетной функции для последующего time. So, если x = 0, то значение функции всегда будет равно нулю. Поэтому условия поверхности всегда соблюдаются. Здесь мы описываем уравнение расширенного распределения температуры (37А) и в то же время можем разделить Интеграл на 2 части с границей 5 = 0.
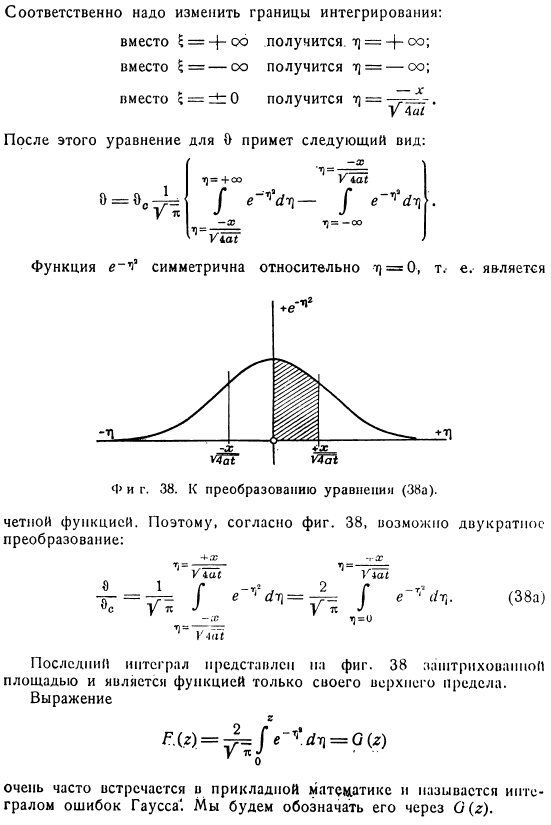
Если учесть, что функция P (;) для положительных значений 5 всегда равна-1-0, а для отрицательных значений 5 равна 0, соответственно、 Вводятся новые переменные интеграции, настройки Поэтому необходимо изменить границы консолидации. для 0 принимает вид: Функция e — ^симметрична относительно m} = 0.In другие слова、 Даже функция. Поэтому, согласно фиг. 38, двойное преобразование возможно: Последний Интеграл показан на рисунке 4. 38 является заштрихованной областью и является функцией только верхней границы. Выражение е В прикладной математике это очень распространено и называется интегралом ошибки Гаусса*. Он обозначается буквой C ®.
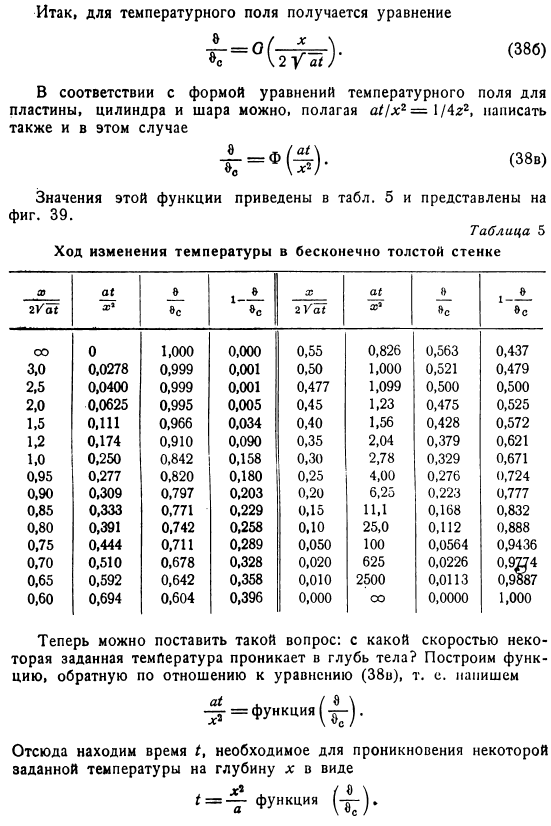
Итак, для температурного поля получим уравнение По форме уравнений температурного поля пластин, цилиндров и шариков можно также описать этот случай, установив / / / / / x2 = 1 / 4r2. ^ =Φ (^)- (38 «) Значения этой функции перечислены в таблице.5-39. Таблица 5 Бесконечно толстое изменение температуры стены Теперь можно задать следующие вопросы: насколько велика скорость, с которой определенная температура проникает вглубь тела, создает обратную функцию по отношению к формуле(38С).То есть, опишите его как= Function (±).
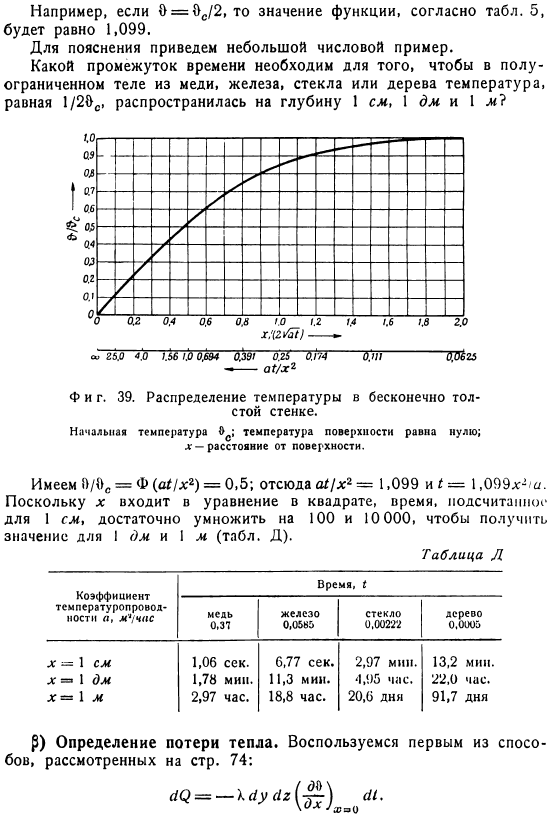
Отсюда мы находим время, необходимое для того, чтобы заданная температура проникла в глубину x в следующем виде: =- Функция Например, если 0 = 0s / 2, то согласно таблице, значение функции. 5 равно 1,099. Для наглядности приведем небольшой численный пример. С полуограниченным объектом из меди, железа, стекла или дерева, как долго необходимо, чтобы температура 1/20 секунды распространилась на глубину 1 см, 1 ДМ, 1 м? См 25.0 40; .5б / .O. 0. 594 0391 02 $ bn bp&25 — ах / Х2 Тоже фигура. 39.Распределение температуры бесконечно толстых стенок. Начальная температура/температура поверхности равна нулю. X-это расстояние от поверхности.
Поскольку x входит в уравнение 2 степени(время, которое вычисляется для I см), достаточно умножить 100 и 10000 раз и получить значения I dm и 1 m(таблица D). Таблица е Коэффициент теплопроводности a, m’; время 1ч 1 Медь 0,37 железо 0,0585 стекло 0,00222 дерево 0,0005 X = 1 см 1.06 секунды 6.77 секунды 2.97 минуты 13.2 минуты л = 1 ДМ 1.78 мин 11.3 мин 1.95 ч 22.0 ч х — \ м 2,97 часа. 18.8 часов 20.6 в 91.7 дней Р) определение теплопотерь. Используйте первый метод, описанный на стр. 74.
- Поскольку распределение температуры не зависит от y и r, в плоскости K2: если x = 0, то экспонента равна 1. Это указывает на то, что теплопотери, проходящие через поверхность, называемую единицей времени, изменяются, когда 1-я принимает бесконечно большую величину, соответствующую 1-му моменту. Количество тепла, выделяющегося из тела за ограниченное время от 1 = 0 до/ = / 0, определяется интегралом. Таким образом, количество выделяемого из организма тепла пропорционально увеличивается. Значение UHer чисто Физическая константа. Используйте обозначение b.
Это значение называется коэффициентом теплового проникновения, но его можно назвать накопительной емкостью O, так как оно становится понятным при рассмотрении задач b и 7.Размеры этой величины, а значит и единица измерения — ккал! М2 * град-час ’ 1. Поэтому против жары дали、 Е = — (39б) Сравнение коэффициентов температуропроводности a = X / sr и теплопроводности^ = |ЛХср показывает, что влияние объемной теплоемкости проявляется по-разному. Поэтому вопрос выбора материала для утепления стен должен решаться соответственно по-разному.
Если пар заключен в сосуд, стенки которого имеют температуру ниже температуры насыщения, на стенках начинается конденсация пара. Людмила Фирмаль
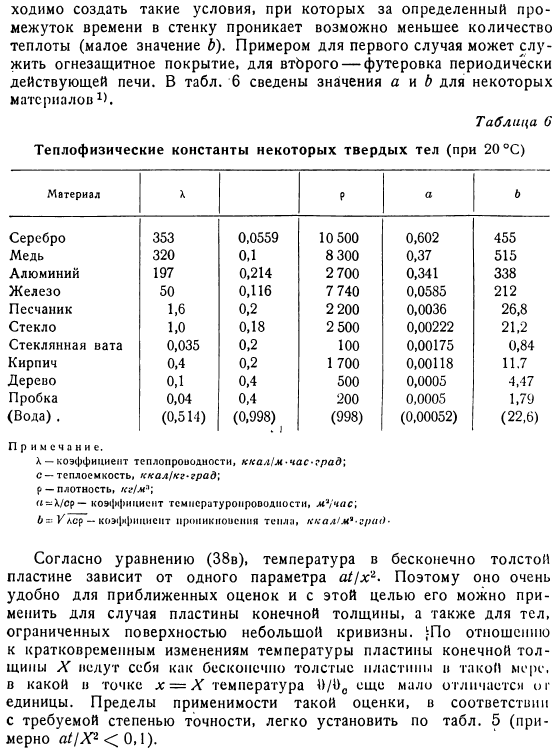
Необходимо ли обеспечить медленное распространение начальной температуры (величина а мала) или необходимо создать условия, при которых тепло не проникает в стенки максимально в течение определенного периода(величина в мала). примером первого случая является огнезащитное покрытие.2-й корпус-это футеровка печи, которая работает periodically. In стол. На рис. 6 приведены значения A и b для некоторых материалов.
Таблица 6 Теплофизическая постоянная некоторых твердых тел (20 ° С) Пожалуйста, обратите внимание Л-коэффициент теплопроводности, kcal1m час-град ’、 с-теплоемкость, ккал / кг-град P-плотность,/ г / Ла. «=Х / СР-коэффициент температуропроводности, м ^времени、 6 = / ler-коэффициент теплового проникновения, ккал / М’ — Град Согласно формуле (38c), температура бесконечно толстой пластины зависит от 1 параметра, atx2, что очень удобно для аппроксимации. Для этой цели его можно применять в случае пластин конечной толщины или в случае объектов, окруженных поверхностью малой кривизны.
Что касается кратковременных изменений температуры, то пластина с конечной толщиной X ведет себя как бесконечно толстая пластина с x = X, где температура 0 / 0o все еще сильно меняется в единицах r. пределы применимости такой оценки можно легко установить из таблицы в зависимости от требуемой степени точности. 5 (о L / / A7 0.1). 1) изучен также случай любого начального распределения температуры.
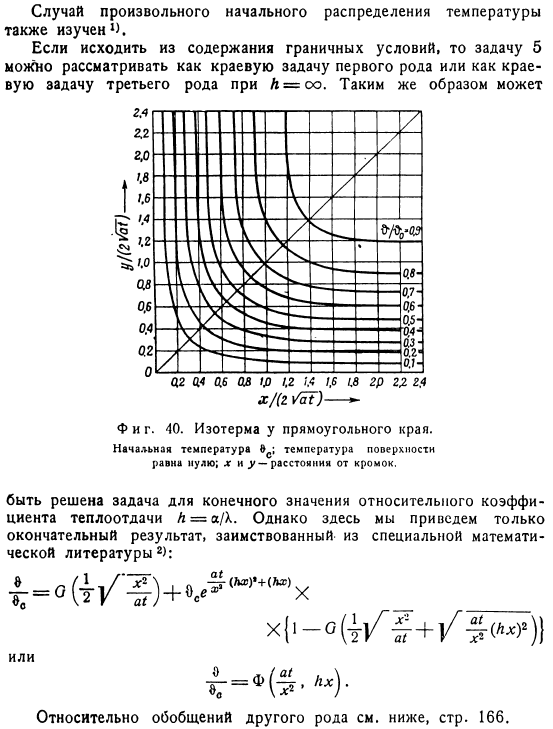
Исходя из содержания граничного условия, задачу 5 можно рассматривать как краевую задачу типа 1 или краевую задачу типа 3 типа Λ=°°.Вы можете сделать то же самое. Тоже фигура. 40.Изотермы прямоугольных концов. Начальная температура Es; температура поверхности равна нулю. X и. y-расстояние от края. Относительный коэффициент теплопередачи K = .a. решена задача о конечном значении 1 \.Однако здесь мы покажем только конечный результат, заимствованный из специальной математической литературы 2).
Или Для различных типов обобщений см. Следующие стр. 166. j) многомерное problem. As уже упоминавшееся на стр. 92 решение формата (386) и, следовательно, (38С) может быть использовано для многомерных задач, например, для торцевых поверхностей длинных цилиндров или прямоугольных стержней. На рисунке 40 показано семейство Изотерм на краю определенного прямоугольника тела очень большого размера, начиная с i/ 0, и температура поверхности поддерживается на уровне 0, в предположении, что температура всех точек тела равна 0c. эти изотермы получены с использованием рисунка 1.
Смотрите также:

