Оглавление:









Температурное поле стремится к равновесию. Шар
- Радиусные шары излучают тепло в окружающую среду через всю внешнюю поверхность. Коэффициент теплопередачи равен A. температура окружающей среды 0 считается нулевой. Начиная с 0, шар везде имеет одинаковую температуру 0°. Кроме того, предположим, что физические константы X, c и p, а следовательно, и a, равны constants. As в зависимости от времени, необходимо определить тип температурного поля и величину теплопотерь. а) математическая постановка задачи. Поскольку температура зависит только от r, используя сферическую систему координат. Дифференциальное уравнение. Первоначальное условие-о * = о = 0С по 0 г И. Р) определение температурного поля.
Заменять это приводит к известному уравнению φ ® (IIc).Решение этого уравнения также известно: Первое решение-это странная функция, поэтому она не подходит для этой задачи. Поэтому остается только решение формы величина n определяется по состоянию поверхности Первые 4 маршрута этого трансцендентального уравнения сведены в таблицу. 4. В общем решении определите только коэффициент Ok. Это можно сделать, используя начальные условия Таблица 4 Корень уравнения Используя слегка измененную формулу (15а), вы получаете: вводя обозначение st, вы достигнете следующей точки в температурном поле.
Проволока нагревается электрически, труба охлаждается снаружи, и измеряются тепловой поток, температуры проволоки и трубы. Людмила Фирмаль
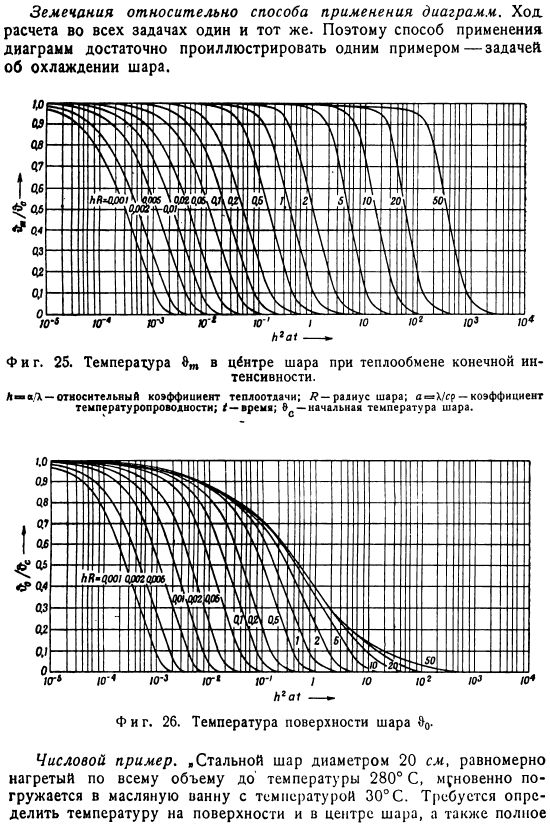
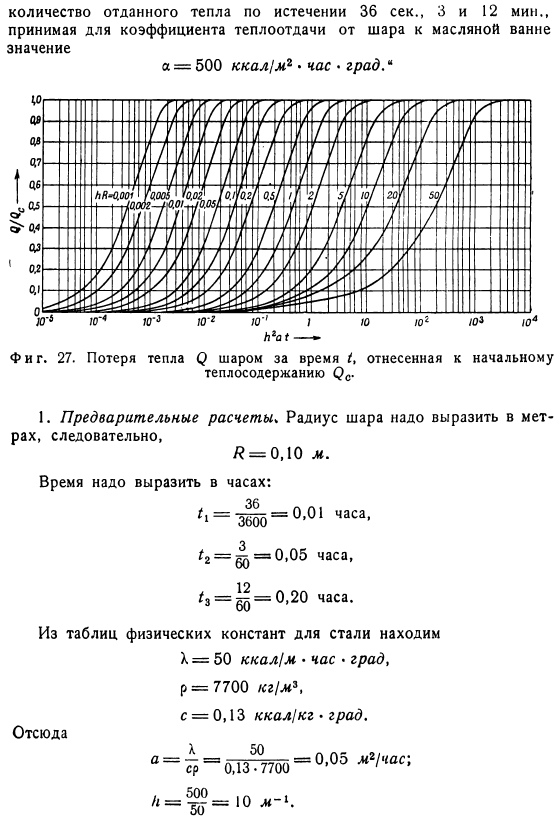
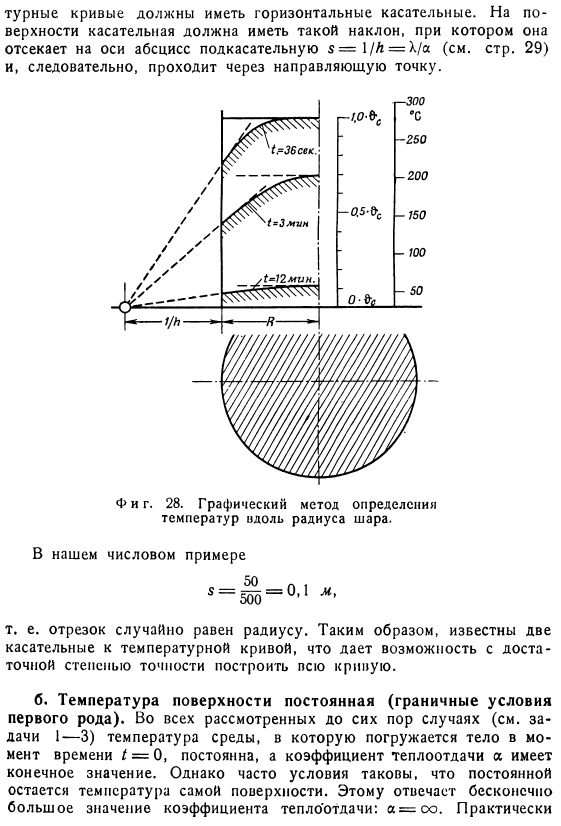
В частном случае AE = oo, 81pool =0.И так оно и есть.、 Чтобы определить температуру центра шара, необходимо принять r = 0 в Формуле (31a).В дальнейшем、 Температура поверхности, R = /?Вы можете получить его, установив его. Подобный этому Т) определение тепловых потерь с}.Формула cp (&c -&) (IV) Класть С интеграцией всего шарика、 Или ^ = Ци^) — 34б> Температура центра шара ($ w) и температура его поверхности (&0) показаны в виде кривой на рисунке 2.Согласно расчетам Бахмана с использованием переменных L /-25 и 26 и H. 2a1.Теплопотери (2) показаны на рисунке 27. Полукруг по способу нанесения рисунка.
Движение. Расчет во всех задачах один и тот же. Поэтому достаточно объяснить, как применить рисунок в Примере 1, то есть проблему охлаждения шара. К2 а!—- *- Тоже фигура. 25.Температура шара при теплопередаче конечной интенсивности # T8 центр. La / X-относительный коэффициент теплопередачи; P-радиус шара. И » X / sr-коэффициент температуропроводности; / time; / C〜начальная температура шара. Пример числового значения. «Стальные шарики диаметром 20 см равномерно нагреваются по всему объему до температуры 280 ° С и мгновенно погружаются в масляную ванну с температурой 30 ° C. It необходимо измерить температуру поверхности и температуру центра шара, а также общую температуру.
Возьмем значение коэффициента теплопередачи от шара к масляной ванне, количество тепла, переданного через 36 секунд, через 3 минуты и через 12 минут а= 500 ккал] м2 * время * город* Тоже фигура. 27.Потери тепла C) шаром в течение времени/, см. начальное количество тепла^ s. 1.Предварительный расчет*поскольку радиус шара должен быть выражен в метрах、 I = 0,10 м Время должно быть выражено в часах. Из таблицы физических констант стали Отсюда 0,05 м2 / час; 2.Вычисление критерия по найденным значениям. Затем вычислите значение fs ?0 = 4•1 ^ 3 •13•7700•280-30)= 1047 ккал. 3.Окончательный результат.
Из диаграммы видно соответствующее опорное отношение 0o / 0v, 0t / 0s и 0!Найдите ОС (&&=280°С-30°С= 250°С) и вычислите температуру О ’ в соответствии с уравнением & ’= 30ч-250 ^ — в°C Для удобства полученные значения суммируются в таблице. Температура поверхности, ° С217. 5 135 45.0 Центральная температура, ° С278 202.5 60.0 Количество отданного тепла, ккал 126 492 963 4.Изменения температуры вдоль radius. In в большинстве случаев при решении технических задач с охлаждением достаточно выяснить температуру поверхности и Центра.
Однако, если вам нужно выяснить все распределение температуры, лучше всего использовать следующие графические методы: (Этот метод также объясняется на примере шара, но он может быть применен таким же образом для цилиндров и пластин.) Поставим его на край радиуса отрезка шара, соответствующего значениям & 0 / 0o и 0t / & 0(рис. 28).Температурная кривая должна проходить через вершины этих вертикалей coordinates. In центр, благодаря симметрии, температурной кривой должен иметь горизонтальную касательную линию. На поверхности касательная должна иметь такой наклон, чтобы она пересекала касательную 5 = 1 /Л=Х/а по оси абсцисс (см. стр. 29) и проходила через направляющую точку. Тоже фигура.
Графический способ определения температуры по радиусу шара. В числовом примере $ = ^ = 0> 1 Это означает, что сегмент случайным образом равен радиусу. Таким образом, известны 2 тангенса к температурной кривой, и вся кривая может быть создана с достаточной точностью. b. температура поверхности постоянна(граничное условие типа 1). во всех рассмотренных до сих пор случаях(см. задачу 1-3) температура среды, в которую погружен объект во времени I = 0,постоянна, а коэффициент теплопередачи a имеет конечное значение. Однако во многих случаях температура самой поверхности остается постоянной. Это соответствует бесконечно большим значениям коэффициента теплоотдачи: а = oo.
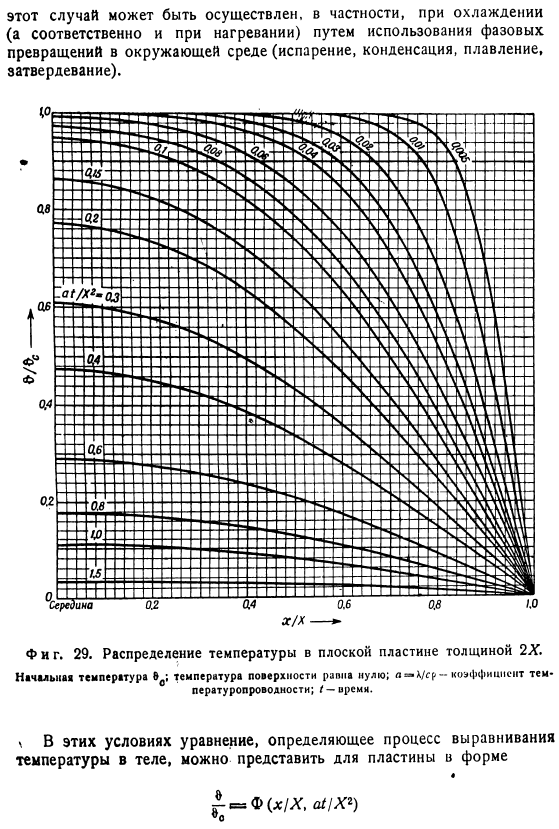
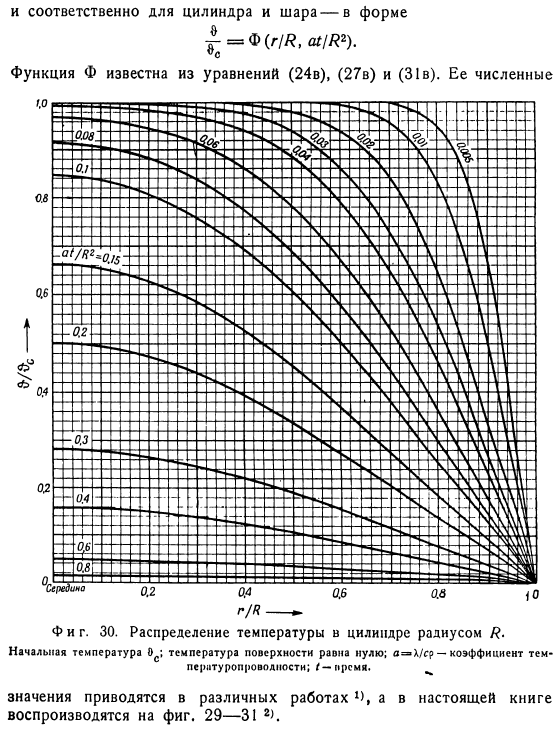
На практике этот случай может быть реализован при охлаждении (а следовательно, и при нагревании) с использованием фазовых переходов (испарение, конденсация, плавление, затвердевание), особенно в окружающей среде. Тоже фигура. 29.Распределение температуры плиты с толщиной 2X. Начальная температура Eo; температура поверхности равна нулю. a-X / sr-коэффициент теплопроводности; / — время. \В этих условиях уравнение, определяющее процесс выравнивания температуры в теле, может быть выражено для пластин вида: F(х / х, / Х2) А для цилиндра и шара соответственно-в виде г //?—— Тоже фигура. 30.Радиус/?Распределение температуры в цилиндре.
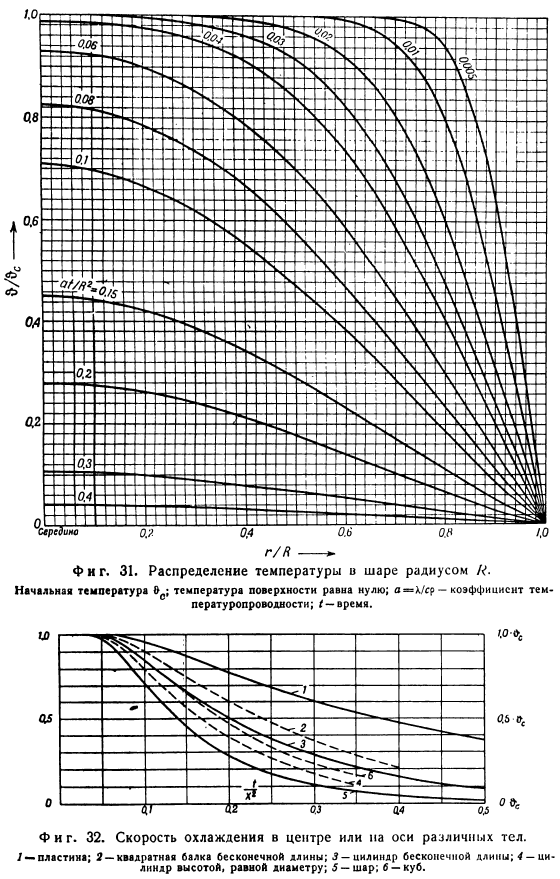
- Начальная температура/температура поверхности равна нулю. Коэффициент теплопроводности; I-время. Значения приведены в различных частях 1>и воспроизведены на рисунке 1 в этой книге. 29-31 2. Тоже фигура. 31.Радиус/?Распределение температуры шара. Начальная температура/температура поверхности равна нулю. a = k / sr-коэффициент теплопроводности; / — время. Тоже фигура. 32.Скорость охлаждения по центру или оси различных объектов. / — □Упругая; 2-квадратная балка бесконечной длины. 3-цилиндр бесконечной длины; 4-цилиндр равной высоты с диаметром; 5-шар. Ъ-кубик На рисунке 2 показаны температурные кривые для осевого и среднего времени.
Соотношение площади поверхности и объема увеличивается, скорость охлаждения увеличивается. Таким образом, шар остынет быстрее всего, а тарелка остынет медленнее всего. Сравнение двух кривых на фиг. Критерии 1>18-27 с тем же числовым значением. c. размещение пространственной температуры field. At 6-й во втором рассматривался только в том случае, если тепловой поток направлен в 1 определенное направление.
Теплопроводность газов часто измеряется методом Сутерлен-да, где платиновая проволока встроена вдоль оси капиллярной трубки, заполненной газом, который надо исследовать. Людмила Фирмаль
Однако полученное решение также может быть распространено на 2-D и 3-D нестационарные тепловые потоки, например, цилиндр конечной длины или parallelepiped. In в дальнейшем возможность такого обобщения доказывается на примере двумерного поля с постоянной температурой поверхности. Рассмотрим прямоугольный стержень с удлиненной стороной 2X и 27 в направлении 2 так, чтобы эффект конечного эффекта можно было игнорировать. Пусть стержни везде имеют одинаковую начальную температуру$ s. In кроме того, он начинается с момента 2 = 0 и поддерживает на своей поверхности температуру, которая считается нулевой.
Затем, в процессе выравнивания температуры, дифференциальное уравнение Граница условная если x = + X и y — ^ 7, 0 = 0 И начальные условия Если 2 = 0, ТО 0 = 0. Для 1-мерного поля, то есть для бесконечной пластины толщиной 2X или 27, решение равно 0x / 0s = 1) читатель может неправильно понять, что относительная поверхность шара является самой большой, а относительная поверхность пластины-самой маленькой. Конечно, это не совсем так. Напротив, в действительности, как известно, шар имеет наименьшую относительную поверхность. Если вы сравните кривые охлаждения (или нагрева) объекта на одной и той же поверхности, то сразу увидите, что скорость изменения температуры шара самая низкая.
Соображения, описанные в тексте, относятся к случаю совпадающего тела, основанного на равенстве размеров decisions. In такое сравнение (например, изменение температуры сравнивается в центре шара с радиусом? А на оси бесконечно длинного круглого цилиндра того же радиуса или толщины 2?На центральной плоскости пластины), тело фактически расположено в том порядке, который соответствует рисунку 2. 32.- Приблизительно. = Φ(χ/о, σ//)) или/ /и C =Φ(г / г, А1 / У2).Эти решения показаны на рисунке 4. 29.Пожалуйста, подтвердите Является решением дифференциального уравнения(35).
Для этого используют частные производные предыдущего выражения. Подставляя дифференциальное уравнение(35)、 (35А) По предположению, он удовлетворяет соответствующему 1D Фурье equation. So, уравнение (35a) является тождеством, и поэтому рассматриваемое произведение является правильным решением. Граничные условия также выполняются. Это происходит потому, что на поверхности 1 из 2 факторов всегда равен нулю. Соответственно, показана возможность рассмотрения трехмерного случая (прямоугольный параллелепипед, цилиндр конечной длины).
Если одна из граничных граней отделена, то расстояние от этой границы принимается равным половине толщины (например, X), поэтому полное значение этого расстояния подставляется в критерий. Этот метод не применим к граничным условиям. Однако он эффективен в условиях конечной интенсивности теплопередачи и в случае неограниченного тела с одной стороны (например, конец очень длинного стержня в прямоугольном или цилиндрическом сечении, конец стенки и т.).
На основе этого метода Бергер 1 > рассчитал температурное поле кубоида при теплообмене конечной интенсивности, Ньюман 2)определил температуру поверхности и Центра различных объектов, Олсон и Шульц3) далее предоставил очень точную таблицу средней температуры, плоскости цилиндра при a = oo и стенки конечной толщины.1 согласно Уильямсону и Адамсу, построены 32 такие кривые. Baer 4>дал приближенный метод, в котором используется только первый член ряда, полученный точным решением. Пример числового значения. Диаметр 2 /?Цилиндрический контейнер= 10 см (i = 0,05 м) и высотой 2X = 16 * si (X = 0,08 м), погружают в кипящую воду при температуре 100°С для стерилизации содержимого.
Начальная температура составляет 20°C. влияние стены незначительно. Контейнер заполняется влажной пастой, для которой a = 6.0-10-4 м2 / час берется. Через 1 час (I = 1 час) необходимо определить температуру самой холодной точки (середины) с комплексным подводом тепла (включая дно и крышку). Рассчитать обоим критериям — =6.0 10-4. 1 = 0,094 и-= −6.0:10-4.1 = 0.24。 Х2 64-10″ * /?2 25-10″ * Эти значения аргументов получены из рисунка 1. 29 (для пластин и из рисунка 30 (для цилиндров), безразмерная разница температур в точке x / X = 0, соответственно r //?= 0: — L = 0,96 и-L = 0,4. > с Отсюда мы видим y = 0.96 0.4 = 0.384. Дело в том, что = 100°С-20 ° С= 80°makes составляет= 31,7°С.
Наконец, мы находим 100-31. 7 = 68,3°C для желаемой температуры. Этот численный пример, как показано на фиг. 2. 32 указывает, что эффект торцевой поверхности будет заметен только тогда, когда As установлен ниже(стр. 450).Закон теплопроводности также эффективен для диффузии.
Смотрите также:

