Оглавление:












О согласовании с начальными условиями
- Задача здесь состоит в том, чтобы построить общее решение из такой характеристики решения. Кроме того, общее решение задачи t = 0 состоит в том, что данное произвольное. Начальное распределение температуры. Поэтому мы говорим о расширении любой заданной функции с точки зрения вибрационных функций. Используйте функции синуса и Косинуса, а также функции Бесселя нулевого порядка типа 1 и типа 2 для ограничения представления любой функции. a. ряд Фурье указанного типа параметра. Рассмотренные здесь соображения дополняют решение проблемы введения (см. стр. 41). Проблема заключается в том, что интервал-X.
Функция F (x), необязательно указанная в xX, должна быть расширена до ряда в виде выражения (m) (см. стр. 41). {{Cᵢsin (ИФО (х) 4-£ > ᵢcos (ПХ) Дж. (14) Как и бесчисленное множество В этом случае значение u является уравнением (u’) и — И+ ^ — = C, G (ⁿ-O- Если окажется, что коэффициенты Скоэффици и о могут быть определены таким образом, что уравнение удовлетворяется для каждого значения X, которое находится между±X и-X, то задача решается. Вспомогательное оборудование formula. In чтобы не прерывать будущий поток вывода, вы должны сначала вывести некоторые вспомогательные формулы. Неотъемлемый.
Результаты обработки опытов, произведенных Бекманом и Селшоппом на цилиндрических слоях и другими авторами на плоских слоях, хорошо совпадают со сплошной линией. Людмила Фирмаль
Дж «грех (х т х) грех (mₖx) ДХ Используя тригонометрическую формулу грех грехом₽= 1 {соз(а -) — ₽Кос(А4 -₽)) Преобразовать в целое число J в {соѕ (м-mₕ) х-с08(LХ+ -»*) х / ДХ. Равный добро пожаловать на наш сайт! Применять тригонометрические формулы грех (В+ П)= грех, потому что п ЮЖД потому что грех п、 Приведите: эту формулу к виду о м * грех (ptsX), потому что (tkX) — — — МТ грех (м * х) Кос(микс) значения mₜ и mk следует выбирать в соответствии с условиями surface. So из уравнения (s) t₁sov (Т, Х) грех (Л1; л) добро пожаловать на наш сайт.) — Ля Соответственно м, потому что (mₖX) грех (mₜX)=mₜcos(Т, Х) грех (mₖX).
Таким образом, интегральное значение произвольно выбранного решения(любого индекса I и A) всегда будет равно нулю, за исключением случая to, m,= m. Когда Ноль. Если i = a, то Интеграл Поэтому в данном случае Интеграл не равен zero. So получаем первую вспомогательную формулу Дж » грех (МНР) грех (/НП:) ДХ = 0 при I + К-Х З = А> 0 2-я вспомогательная форма оценивается точно так же.
3-е вспомогательное выражение имеет следующий вид: Определение коэффициентов С и₍Dₜ.To Сдай назад.」 P ( * ) = +Sin Sin ( «,*) + — с* Sin ( » * * ) + −4- + Д, Кос(н | х)+ * Dₖcos(п * х)+ 1. Определите один из коэффициентов, например оба parts. It необходимо умножить уравнение (tn x) dx и интегрировать его на пределе: от-X до+ — X. допустимо (нет Предок Допускается консолидация терминов по сериям по терминам. И затем…
Согласно 3 вспомогательным формулам, в правой части уравнения исчезают все интегралы, за исключением интегралов, содержащих sin2 (miX). Вы можете ознакомиться с в следующем формате Для определения коэффициента естественно умножить обе стороны формулы (14) на cos (n, x) dx. Затем, используя тот же расчет, что и Cp, формула Если таким образом определить все коэффициенты C и Dₜ, то бесконечный ряд справа от уравнения (14) фактически дает значение функции F (x) в интервале-X x + — X.
Строго говоря, необходимо определить бесконечное число коэффициентов. Однако для всех часто встречающихся функций F (x) ряд сходится довольно быстро(поскольку В любом случае, это слишком далеко.)Поэтому, почти всегда можно ограничиться несколькими членами ряда. b. ряд Фурье в обычном form. In в различных областях физики и техники возникают проблемы с решением и » необходимость расширения данной функции произвольно возникает」 В линии по знаку и Косинусу. Однако, он не установлен Ограничений, аналогичных граничным условиям вида 3, не существует. Полученная серия известна под своим общим названием. Такие параметры, как в данном случае, не ограничены граничными условиями.
Поэтому они считаются равными членам столбца натуральных чисел. Затем, чтобы упростить запись, масштаб оси x Она выбирается так, что X = i. тогда задача формулируется следующим образом: Функция f(х).Произвольно задается через интервалы-й х 4-й, расширяется до ряда форм ^(*)= 2 Син ФА (к) 4-bₜcos(с)}、 Или в развернутой записи Ф (Х)= Sin 0 + — а Sin х + — грех 2×4- ..boscos 0 + b, cos x ±b₂cos 2x + Пока коэффициенты u и b \ произвольны, этот ряд называется тригонометрической функцией и называется рядом Фурье только после определения коэффициентов. Опять же мы используем 3 вспомогательные формулы.
Разница Из того, что было оценено ранее, следует, что величины m₍и n больше не являются корнями трансцендентального уравнения, а являются целыми положительными числами и границами интегрирования. Вместо-Чи 4-х будет-к и 4-й. Вспомогательная формула потому что Ф (ЛК), потому что (КХ) dх = 4tj(потому что (((/- Λ) Х1-потому что [(Z4 в аренду-ФК) х)) ЦТО = Slnf (/- /грех [(+ *) «] Где l и k, а следовательно (l-k) и (( — + * ) — целые числа. В качестве синуса аргумента фактор i всегда равен нулю, а сам Интеграл всегда исчезает со всеми значениями i + k.
Если i = = ft, то 2-я дробь справа от выражения принимает значение, равное нулю. Для первой дроби мы получаем 0: 0, то есть неопределенность. Когда мы обнаруживаем неопределенность、 Хм… (- Я Таким образом, Интеграл будет равен k.
В некоторых случаях, когда I и k отдельно равны нулю, 2-й десятичный знак также принимает значение, равное π, а Интеграл равен 2π.Подобный этому Мы получаем: Дж соз (ЛК), потому что (КХ) D х = 0 для Л Ф К = это я-к> 0 = 2n Л = К = О Аналогичный расчет дает 2 другие вспомогательные формулы. 2.Вспомогательная формула: J sin (Zx) sin (Ax) dx = 0 (Z + a case) = Я З = А> 0 = 0 З = А = О 3.Вспомогательная формула: J sin (Zx) cos (Ax) dx = 0 для i =#k = 0 я = к> 0 = 0 Л = К = 0 Определение коэффициентов» для определения одного из коэффициентов, например, Lk, необходимо умножить обе части тригонометрического ряда на C0s (Ax) dx и проинтегрировать его от—l до -+». И затем…
Я найду его здесь. = Ф (Х) с COS (КХ) dх. Точно так же、 。 Оба выражения справедливы для всех значений k, за исключением значения ω= 0 (см. вспомогательные выражения (I) и(2), 3-й случай).Коэффициент₀ всегда равен нулю. Для Коэффициент b0 должен принимать специальную формулу. Обычно, чтобы избежать этого Замените ряд тригонометрических функций рядом вида Все коэффициенты C; и O (в том числе; их и делают, можно n определите выражение ввода-вывода 。 (176 )) Формула (16), коэффициент! Формула для *определяется в соответствии с формулами (17a) и (176) и называется рядом Фурье. Дирихле conditions. In предыдущий вывод, 2 предположения были неявно приняты.
Согласно первому из них, оба интеграла На самом деле, оно имеет конечное и однозначно определенное значение. 2-е предположение можно сформулировать следующим образом: Интеграл бесконечно малого ряда равен сумме его отдельных интегралов. Члены, поэтому ряд может быть консолидирован на срок. Эти предпосылки есл! Функция F (x), хотя и очень распространенная, удовлетворяет*общности. Эти условия называются условием Дирихле и указывают на следующие состояния: 。Функция интервала-K x — / — MC F (x) должна быть четкой, конечной и интегрируемой everywhere. In этот интервал, максимальное значение конечного числа Только минимальное и конечное число точек прерывания непрерывности.
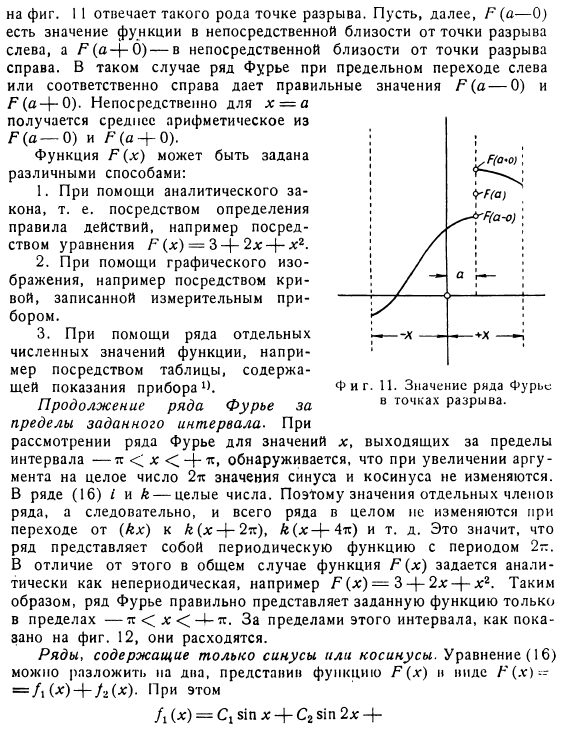
- Обратите внимание на следующее: В некоторых местах могут быть пробелы в функциональности. Значение Х = а Рисунок 2-11 соответствует этому виду Breakpoint. In кроме того, предположим, что вы помещаете F (a — 0) значение функции непосредственно около левой точки разрыва, A / (o-j-O) в непосредственной близости. От точки разрыва до right. In в этом случае предел или ряд Фурье при каждом переходе вправо дает правильный F (a- | −0). x =если среднее арифметическое получено непосредственно Ф(О −0) и Р(О + 0). Функция F (x) может быть определена по-разному. 1.Используйте аналитическое правило. То есть определите правила действия, например, используя уравнение F(x)= 3 — + 2x-+ xr.
Например, используя кривые, записанные измерительным прибором, используя графическое изображение. 3.Например, используйте таблицу, содержащую измеренное значение*, и набор отдельных чисел для функции. Рассматривая ряд Фурье значений предела продолжения ряда Фурье с заданным интервальным пределом В случае интервала-i x — | — i мы можем видеть, что 2-е значение синуса и Косинуса не изменяется, даже если аргумент увеличивается на integer. In ряды (16), I и k являются целыми числами. Отсюда и значение Отдельные члены ряда, а следовательно и весь ряд, не изменяются даже при переходе от (kx) к/ r(x-(-2π), Λ(x-| — 4π) и т. Это потому что серия регулярна 2-ая функция cycle.
При расчетах инженерных конструкций интерес в основном сосредоточивается на определении суммарного теплового потока через слои жидкости различных геометрий от горячей к холодной поверхности. Людмила Фирмаль
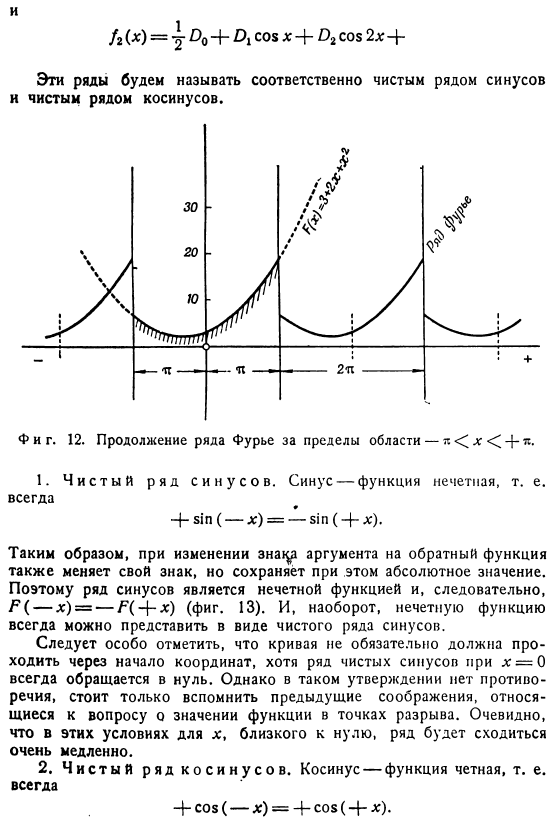
Напротив, в общем случае функция F (x), F (x)-3-|- 2x + — XR определяется аналитически как непериодический. Ряд Фурье является правильным. Представляет только определенные функции в диапазоне 1-1.На внешней стороне этого интервала, как показано на рисунке 3, 12, они расходятся. Линия, содержащая только синус или Косинус. Выражение (16) можно разложить на 2, которые представляют функцию F (x) в виде/-’(x)= / i ( * ) + A (x).при этом Каждый из этих рядов называется Чистым синусоидальным рядом * + грех (- * )=-Син (- х). Таким образом, если вы измените значение аргумента обратно, функция также изменит знак, но сохранит Абсолют value.
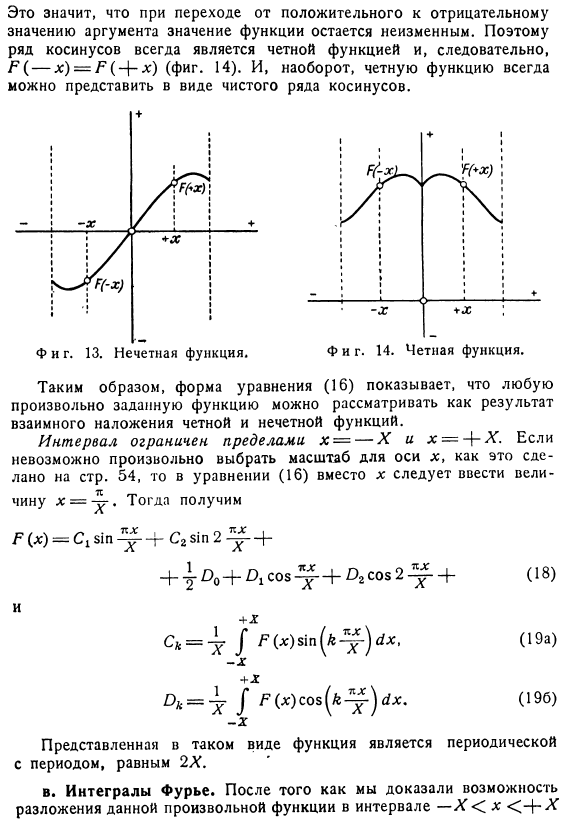
Число синуса является нечетной функцией、 Итак, F (- x)=-Gamma (4-x) (рис.13).Кроме того, наоборот, нечетная функция всегда может быть представлена как чистый набор синусов. Особенно обратите внимание, что необходимо пройти через начало координат. ifcux синуса x= 0 всегда будет исчезать. Однако противоречий в заявлении нет, только издержки Вспомним предыдущие соображения по проблеме значения функции в точке останова. Очевидно, что в этих условиях ряды сходятся очень медленно, если x близок к нулю. 2.Чистый r: всегда Сова хорошо. Косинус-четная функция, т. * соѕ (- •*)= + — COS в (4-х).
Это означает, что значение функции не изменяется при переходе от положительного значения к отрицательному значению функции. argument. So многие косинусы всегда являются четными функциями и、 Таким образом, R (—x)= R ( -+ *) (рис.14).И наоборот, четная функция всегда Таким образом, вид уравнения (16) показывает, что произвольно заданную функцию можно рассматривать как результат взаимной суперпозиции четных и нечетных функций. Интервал ограничен x = — X и x = — \ — X. Если невозможно произвольно выбрать масштаб оси x, как это делается на стр. 54, то вместо x следует ввести его в Формулу (16 Значение х =-^.Тогда вы получите.
Функция, представленная в этом виде, является периодической В цикле, равном 2X. С. Интеграл Фурье. После доказательства возможности расширения этой произвольной функции с интервалом-Х Х + -Х В ряде тригонометрических функций возникает естественный вопрос о том, окажется ли расширение сферы применения рассматриваемого метода справедливым для всех. интервал-оо + — оо. Такие обобщения, безусловно, возможны. Для доказательства см. формулу (18). Подставьте значение C /в эту формулу и формулу(19).Формула (19)описывает, чтобы избежать недоразумений. вместо X. А потом… 。 В этом случае последнее преобразование выполняется по формуле триангуляции грех СФ₽Н ₽ + — потому что Потому= потому что(A -₽).
Как упоминалось выше, Косинус-функция обоих членов может быть объединена в 1, Если: Но… И так оно и есть.、 От A == + −1 до k = + — oo, но от A =это означает, что первый член включен Качество к =0.И так оно и есть.、 Создание бесконечного количества Очевидно, что при неограниченном увеличении X и k значения ir / X очень малы. он представлен dq (и соответственно、 от K — ^ — м Бесконечное количество становится интегралом、 Выражение (20) является выражением fu, заданным в Интеграле Фурье.
Однако следует подчеркнуть, что выражение (20) справедливо только при условии, что для всех значений-ooh + sy Если указанная функция f (x) удовлетворяет следующим требованиям: 1) везде должно быть непрерывно и ясно. 2) Вы можете иметь только конечное число максимумов и минимумов. 3) неограниченное увеличение (по абсолютной величине) в x, потому что вам нужно очень быстро приблизиться к нулю, Интеграл Дж. Ф (Х) DX Он оставался конечным. Математический анализ этих ограничений выведет нас за рамки данной книги. Интегралы Фурье четных и нечетных функций.
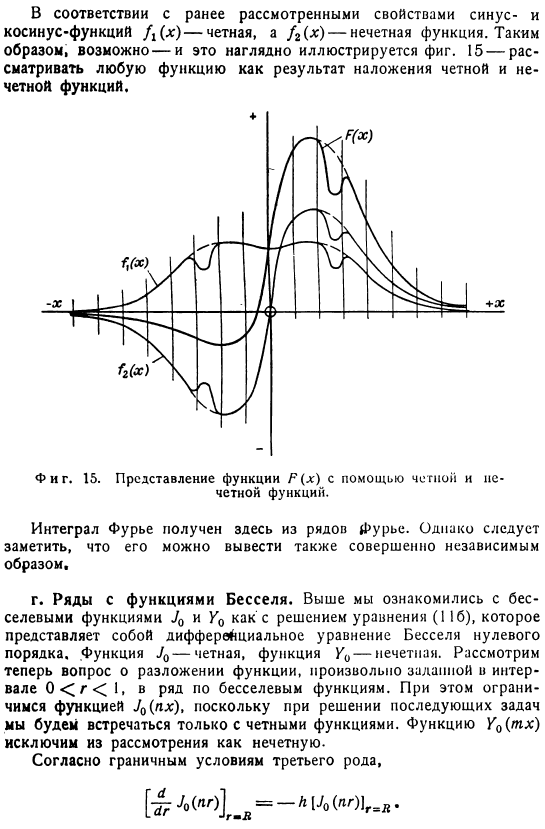
Используйте тригонометрические формулы_ Формула (20) Это уравнение можно разложить на 2 и представить его левую часть в виде R (x)= / i ( * ) + A (x). Согласно характеристикам ранее рассмотренных синусоидальных и косинусоидальных функций, f (x) является нечетной функцией, а f (x) — нечетной функцией. Таким образом, это возможно, и это четко показано на рисунке 2. 15-рассмотрим любую функцию как результат наложения четных и нечетных функций. Где интеграл Фурье получается из ряда Фурье. Однако он также может быть получен совершенно независимым способом.
Бессель занимает место с features. In выше мы привыкли к функциям Бесселя Jₒ и Yo как к решениям уравнения (116), которое является дифференциальным уравнением Бесселя. Следующий ноль. Функция Jₒ Четна, а функция Y0 нечетна. Теперь рассмотрим задачу о разложении произвольно заданной функции в интервале 0r I множества функций Бесселя. В этом случае мы ограничиваем функцию J₀ (nx) четным числом, поскольку при решении последующих задач возникает только четное число функций.
Исключить функцию K2 (mx) из рассмотрения как нечетную По граничным условиям вида 3. 1л» («)],. «• Однако из Формулы дифференцирования функции Бесселя ясно, что X (*) =- A (*)>.Где A ( * ) — функция Бесселя 1-го класса. Основываясь на этом уравнении, предыдущее уравнение Принимать форму Это бесконечное число корней n, pc, как показано на стр. 49…С трансцендентных уравнений.
Ниже приводится разложение множества функций Бесселя: (22) Чтобы определить коэффициент Dₖ, умножьте обе стороны уравнения на rJₐ (nₖr) dr и интегрируйте его от r = 0 до r = +1.Тогда мы получаем На основании 3 вспомогательных формул, аналогичных приведенным выше, можно сделать вывод, что все термины, кроме тех, которые включены справа, исчезают. Джей?( — ).Однако из теории интегрирования функции Бесселя、 Таким образом, значение Dₖ можно найти в следующем виде: ( Это выражение справедливо для всех значений K начиная с 4 = 1.
Более подробную информацию о представлении любой заданной функции с помощью рядов и интегралов, включая функции Бесселя, можно найти в соответствующей математике Литература.>* В предыдущих 2-х разделах мы рассмотрели необходимые основные физико-математические понятия и методы анализа. Ниже мы опишем отдельные задачи с поля. Соответствующий дифференциальному уравнению (4a) Кроме того, мы ограничиваемся такими упрощенными случаями, когда мощность источника тепла, изменение температуры во времени или оба этих эффекта происходят одновременно. Равный нулю.
Смотрите также:

