Об отыскании частных решений

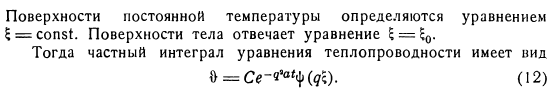
Об отыскании частных решений

• Невозможно предложить общий метод нахождения конкретного решения, но есть еще известные правила, применение которых в большинстве случаев приводит к конкретному решению. Очень. Часто, насколько мы знаем из опыта, ход физических процессов показывает, на какие функции нужно ориентироваться в первую очередь. A математические соображения. Наиболее распространенная форма 1 зависимой переменной i) и 2 независимых 2-х дифференциальных уравнений в частных производных Изменить Это уравнение. с + интернет + ИЖС (6） Это U и V-только функция, а не функция 8.если r= 0, следовательно, уравнение 1-крена, далее, коэффициенты 1, m, q являются постоянными значениями, присваиваемыми.

Это всегда приводит к определенному интегралу. Чтобы доказать, найдите производную (8） Дифференциальное уравнение (b) Ce’uesv выражение сводится、 / a2+ mag + 2_ / _ od? О.₌ Это уравнение называется уравнением коэффициента. Здесь видно, что если воздух выбрать следующим образом, то подстановка (7) будет Интегралом дифференциального уравнения (6). Так что условие (8) является satisfied. So, можно произвольно выбрать не только C, но и 2 тома a или p.

В области двух пограничных слоев характер изменения температуры подобен обнаруженному в свободном конвективном пограничном слое на отдельной вертикальной поверхности. Людмила Фирмаль

После этого из уравнения определяется другая сумма (8).Поскольку выражение (8) является выражением 2, в зависимости от характеристик этого дискриминанта, либо 2 разных действительных корня, либо 2 идентичных действительных корня отвечают. Или 2 комплексно сопряженных корня. Поэтому сама интеграция может быть сложной. Для сложных решений это важно. И это не удивительно, потому что оттуда вы можете получить 2 реальных решения. Подчеркните реальную и чисто мнимую часть решения.

В качестве примера снова рассмотрим дифференциальное уравнение Принимая x в качестве координаты в уравнении (6) и r> — время、 Выражение (8) принимает вид: — АГ + + — = 0 или P = АГ Таким образом, уравнение&= Cea, e является Интегралом дифференциального уравнения. Коэффициент теплопроводности а практически положительный value. So, для положительного a2, температура должна расти бесконтрольно с течением времени t.

Добродетель В этом деле Для задач с теорией теплопроводности необходимо применять только значение а, которое дает отрицательный результат ar. It означает, что вам нужно Возьмите фиктивную стоимость. набор а =±СГ. Где q — любое действительное значение, а Интеграл принимает вид: Отсюда, используя известную формулу Вам как комплексные решения. 。 Если вы добавляете оба уравнения и выравниваете реальный и воображаемый стили слева и справа от уравнения: Б,£1 +£1ₑ — » о » что? х),/8₂= е-я’alsin(ц). В 2-е выражение может уменьшить мнимую единицу/.Если указано. Затем снова получите решение (g) и (h) задачи введения. 

Решения дифференциальных уравнений, то есть、 Решение 1 и 2: 9 = Ce — «oe±ⁱ» a」、 Решение 3 и 4: & = Ce — «» ° (qx). Где C и Q-произвольные значения. Стоит отметить, что все 4 решения являются продуктами 2 отдельных функций, от которых зависит каждая из них От 1 переменной. Но известны и особенности, по которым такое разделение невозможно. Например Легко видеть, что это на самом деле интеграл от производной Уравнение. Для этого соответствующие производные и суб Поместите их в дифференциальные уравнения. У нас есть После умножения становится ясно, что они равны друг другу. Решение для использования(6) Это такое выражение. b. физические соображения.

Рассмотрим сначала решение, которое выражается в виде произведения 2-х функций, согласно ранее проанализированному методу анализа. Зависит только от времени t, а от остальных 3 пространственных координат c, 1), C. & = СР(0п&C, с). В настоящее время мы имеем Характер поставленной задачи указывает на то, что необходимо ожидать периодических изменений температуры со временем во всех точках поля. Тогда ф(т） периодическая функция t (см. Раздел 2, стр. См. 109).

• В отличие от этого, если проблема ставится так, что температуры в разных точках имеют тенденцию быть равными, например. Вам нужно выбрать функцию для увеличения Аргумент приближается к нулю asymptotically. In в этом случае естественно рассматривать экспоненциальную функцию с отрицательными показателями. Я тебе верю. = Се -«, ’ φ($.Т). С） Пока что не только C, но и p абсолютно произвольны amount. So вы можете сначала ввести вместо p(на основе результатов, полученных ранее, см. стр. 33） Еще одна произвольная величина согласно уравнению p = qta. Это еще больше упрощает запись form. In кроме того, формула (9а) имеет вид Я найду его здесь..

Если эти выражения подставляются, они могут быть заключены в кавычки »- 。 Дифференциальные уравнения упрощенной формы Итак, если применить экспоненциальную функцию к f(t), то функции φ (Е, ц. Если уравнение можно найти, то получается решение уравнения теплопроводности. Удовлетворяют дифференциальному уравнению(10). Подставляя формулу(9), вы получаете существенное преимущество. Количество независимых переменных уменьшается на 1.То есть, Т опускается. Например, если Температурное поле зависит только от 1 координаты; вместо уравнений в частных производных необходимо решить Обыкновенное дифференциальное уравнение.

Пограничный слой растет вверх на более горячей стенке, в то время как пограничный слой вдоль стенки с низшей температурой растет в нижнем направлении. Людмила Фирмаль

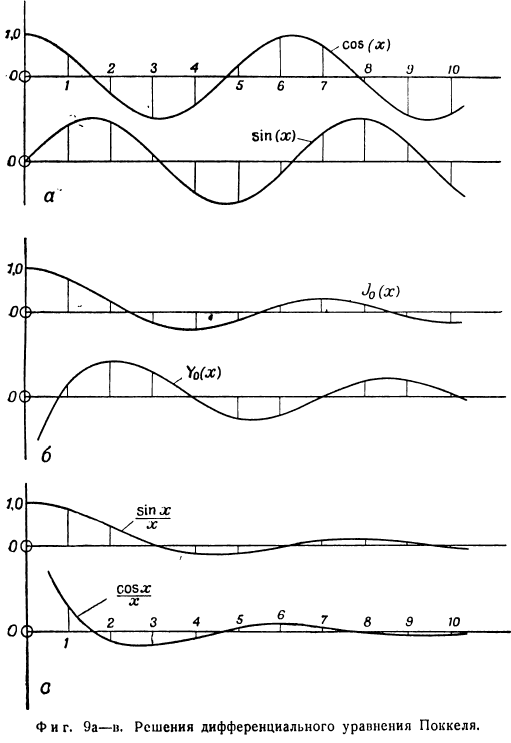
Уравнение (10) часто называют дифференциальным уравнением покера、 Дифференциальные уравнения Лапласа U2f= 0 и дифференциальные уравнения Пуассона V2^ = const являются наиболее важными дифференциальными уравнениями в математической физике. Частных производных. Поэтому характеристики этого уравнения и его решения освещаются в обширной литературе. c. Формула 72f-1 -?2F= 0 для 3 важных специфических cases. In уравнение (10), дифференциальное уравнение покеля еще не было отнесено к определенной системе координат.

С помощью Векторное уравнение (IX) (см. Приложение), это уравнение может быть преобразовано относительно 3 основных систем координат. Во-первых, рассмотрим простейший случай Распределение температуры зависит только от 1 координаты. 。Декарт.(Прямоугольник прямой) координаты. 独立 не зависит от Y и Q. при этих условиях, согласно векторной формуле (1xa), уравнение имеет вид Это решение дифференциальных уравнений, которое может быть легко проверено путем подстановки. Они славятся вибрацией 1) Детали Функция с постоянной амплитудой, то есть, чисто периодическая функция. Рисунок 1 9a представлен для частных случаев C = 1 и q = 1. Цилиндрические координаты. предположим, что φ зависит от r only.

В этом случае векторная формула (1X6) упрощается、 Это уравнение также является осциллирующим решением Функция с аргументами (qr).Однако, как видно из рисунка５, их амплитуда уменьшается с увеличением аргумента. 96. Обе функции называются Бесселем нулевого порядка или цилиндром functions. In в этом случае выделяется первичная функция Бесселя 1-го класса-символ нуля _ / ₀ Порядка 2-го вида-символ Fₒ. Поскольку эти функции не могут быть представлены в виде кратких аналитических выражений, их значения организованы в таблицы, аналогичные таблицам тригонометрических функций. Дифференциальное уравнение(116) называется уравнением Бесселя нулевого порядка. Его решение 。 Сферический coordinates.

В этом случае, если|>зависит только от r, то из векторного выражения (1XB) это выглядит так: Существует 2 решения этого уравнения. Что мы можем определить производные, что мы можем определить производные, что мы можем определить производные, что мы можем определить производные, что мы можем определить производные, что мы можем определить производные, что мы можем определить производные Отнесите их к Формуле (Iv).Эти решения также являются вибрационными features. As аргумент (qr) увеличивается, его амплитуда очень быстро уменьшается、 Амплитуда функции Бесселя(рис. 9С). Простой вывод.

Разложенные конкретные дела очень важны, поэтому их следует использовать в качестве основы для дальнейшего рассмотрения вопроса о согласовании конкретного дела. Интегралы с границей conditions. It показывает, как определяются координаты, чтобы охватить все 3 случая в 1 общем формате во время обсуждения. Затем Или, в другом частном случае, считайте, что это x, r или r. Поверхность с постоянной температурой определяется уравнением£ = const. Поверхность тела заполняет уравнение.

Смотрите также:

• Методические указания по теплотехнике

Краевые условия	О согласовании с условиями на поверхности
Вводная задача	О согласовании с начальными условиями