Вводная задача

Вводная задача

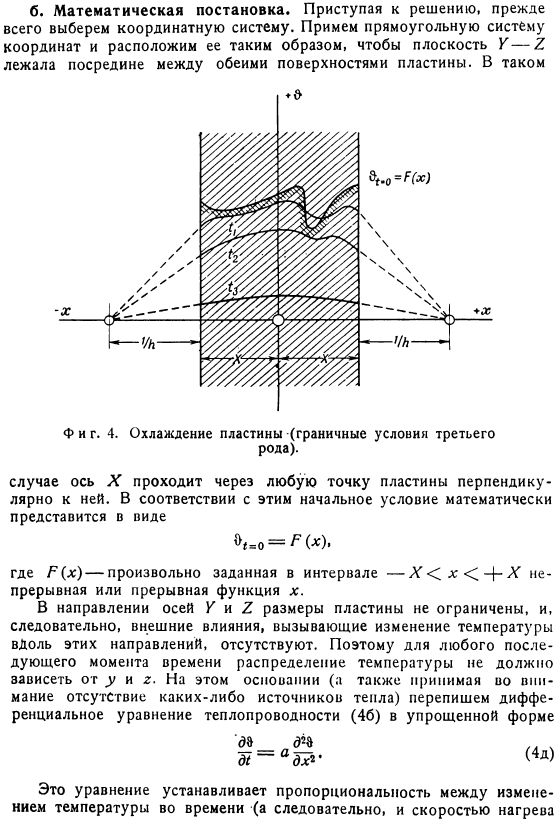
• Содержание задачи. Неограниченная параллельная плоская пластина толщиной 2X, состоящая из вещества с физической постоянной X (Рис. 4). P и c во времени t = 0. Температура каждой данной точки зависит только от расстояния этой точки от распределения температуры обеих внешних поверхностей. Следовательно, поверхностная константа. Температура будет находиться в плоскости, параллельной поверхности пластины. Сама поверхность пластины взаимодействует с температурной средой 0. Относительные коэффициенты. Теплопередача с обеих сторон пластины имеет одинаковое значение a k = h.

Без тепла source. It необходимо определить, как изменяется начальное распределение температуры Под влиянием теплопроводности внутри пластины и теплопередачи через поверхность, с течением времени b. математическое утверждение. Во-первых, чтобы добраться до решения, выберите систему координат. Примите декартову систему координат Y-Z находится в середине обеих поверхностей пластины. Это не так работает. В этом случае ось X проходит через любую точку пластины перпендикулярно it. In в соответствии с этим начальные условия выражаются математически в виде: , = Р(х). Где F (x) — непрерывная или прерывистая функция x, необязательно указанная в интервале-X X.

За исключением области возле края, перенос тепла равен тому, который может быть вычислен для чистой теплопроводности. Людмила Фирмаль

В направлении оси Y и оси Z нет никаких ограничений на размеры пластин. Поэтому нет никаких внешних воздействий, которые вызывают изменения температуры вдоль этих направлений. И так оно и есть. В более поздний момент распределение температуры не должно зависеть от y и R. На этой основе(а также учитывать отсутствие источников） heat) перепишите дифференциальное уравнение теплопроводности(46) в упрощенном виде (4Д） Это уравнение устанавливает пропорциональность с изменением температуры с течением времени(следовательно, скорость нагрева Кривизна распределения температуры представлена 2-й производной относительно пространственных координат.

Коэффициент пропорциональности Он действует как коэффициент термической диффузии А. Граничное условие этой задачи состоит из 2 частей. если x = — \ — X, то вектор gradₙ8 должен быть ориентирован вдоль внешних нормалей, то есть возрастать x. аналогично, x- — X должно принимать направление внешних нормалей относительно града 8, но здесь оно уже соответствует направлению уменьшения X. Так что если поставить 6 =уравнение (5), то можно получить оба граничных условия. Задача о последующем изменении температурного поля уменьшается, выраженная математически в определении 8 как функции переменных x и t и параметров A, A и X. Ниже перечислены 5 уравнений с математическим описанием задачи.

Правильно Тебе нужно решить & =Φ(х, t. А.Λ, Х). (д） c. найти частные интегралы. Для функции температуры сначала найдите функцию, удовлетворяющую только дифференциальному уравнению. Во-первых, попробуйте применить функцию, которая является продуктом 2 функций.1 зависит только от t, а другой 1 зависит только от x. очевидно, что эта функция Следующим образом： Φ (Ф. Х)= |>((х). (ми） Этот метод временно исключает ряд особенностей из рассмотрения.

Однако если такая подмена приводит к решению, то это ограничение не должно ни к чему приводить. Это не проблема, потому что 4 уравнения (a-d) определяют проблему по-своему. Но из этого следует, что кроме результата, других решений быть не может. Конечно, если окажется, что первая подмена не привязана к цели, то следует учитывать и другие особенности. Как обычно, если представить 1-ю и 2-ю производные с p ’(t) и φ «(x), то после подстановки (e) дифференциальное уравнение (a) примет следующий вид: ？ ’(0ph(х)= B>(О «(х). Если вы можете найти функцию с этим свойством.

Где p и q-произвольные постоянные величины, и для этих функций из дифференциального уравнения получаем следующие условия соединения p и q: г в ре’; идти Р = УФ. Такая особенность действительно существует. Из основной формулы дифференциального уравнения мы видим следующее: 1) e, одиночные одиночные дифференциальные концы 2) sin ^ x) двойной дифференциал i Когда двойная дифференциация продолжается 。 Чтобы избежать индекса, напишите m вместо 94 ниже и n вместо qn. По этим причинам, как первая замена、 。 И затем…

Т оказывается связанной с отношениями Если случайным образом выбрать только 2 величины из 1, то остальные значения определяются из степеней свободы выбора последнего уравнения m, в результате чего p = — mr. Итак, уравнение Является решением дифференциальной задачи equations. In кроме того, его левая сторона никогда не будет решением даже после умножения на любую константу C. In факт、 Если вы дифференцируете функцию 1 раз на t и 2 раза на io x, то коэффициент C остается неизменным, поэтому он выпадает из обеих сторон дифференциального уравнения. Выражение (g).он называется частным интегралом дифференциальных уравнений(a).

Аналогично, если функция является Удовлетворяют дифференциальному уравнению, и B = De-cos (пх) (з) Если D-любое число, то оно также является частичным integral. In оба этих решения (g) и(h), система значений m, n и C, D абсолютно произвольны. То есть индивидуальными ценностями являются — выполняет весь ряд чисел от-ОО до — | — со постоянно. Однако такая свобода выбора сохраняется лишь в той мере, в какой уравнения (g) и(h) рассматриваются только как решения. Дифференциальное уравнение. Во-первых, она ограничена условиями поверхности. г) согласование конкретных решений и пространственных граничных (граничных) условий.

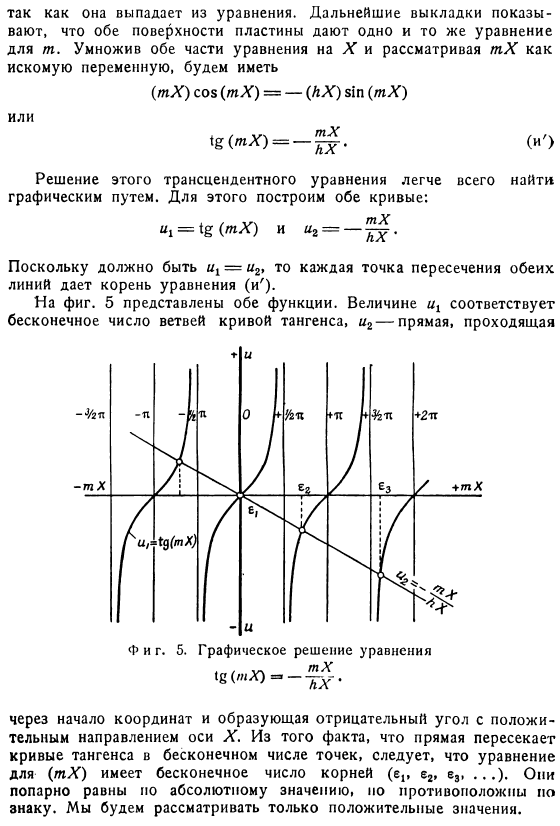
От интеграла По дифференциалу получаем уравнение Подставляя значения этих & и db / dx, вид граничного условия (u (d)) имеет вид: (И） Из этого следует, что, во-первых, пространственные граничные условия еще не ограничивают свободу выбора значения константы С. Дальнейшее вычисление показывает-X дает то же самое уравнение, имея дело с TX Поскольку он выпадает из уравнения, две стороны пластины будут m. умножая обе стороны уравнения, искомая переменная равна Решение этого трансцендентального уравнения легче всего найти graphically. To сделайте это, создайте обе кривые. = «»*>»5- Поскольку» ₁ = «2 должно присутствовать, каждое пересечение обеих линий обеспечивает маршрут уравнения (и’).

• На рисунке 1 5 показаны обе функции. Сумма соответствует бесконечному числу ветвей касательной кривой, y-проходящая через нее прямая линия. Он проходит через начало координат, образуя положительный и отрицательный углы оси X. Из того, что линии пересекают касательную кривую в бесконечном числе точек、 число маршрутов в уравнении (mx) бесконечно(epe₂, e₃,…это не так. Абсолютное значение равно в парах, но знак противоположен. Мы рассматриваем только положительные моменты Значение. Корни находятся в интервале Там нет корня в средней области. Положение корня в указанном интервале зависит от значения(hXy, фиксируется только значение ₁₁0). В таблице.

На рисунке 1 показаны первые 5 маршрутов от значения LX = 0 до значения hX = oo от e до e₆. Значение, такое как Рттг, является уравнением NC = ₍ / ?{. Таблица 1 Корень уравнения Изучается также 2-й Интеграл. б = де-Кос (ПКС). Дифференциал первого порядка Исследования, проведенные на этом Интеграле, сначала показывают, что значение O не учитывается, а затем значение из условия.

В безразмерном прадставлении соответственно в дополнение к числу Грасгофа появляется отношение высоты к расстоянию. Людмила Фирмаль

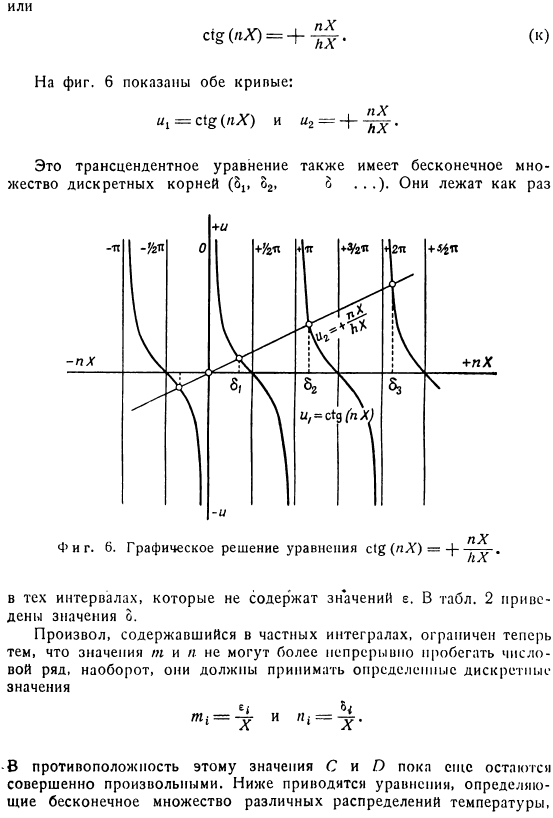
Снова двусторонний уравнение для pX-это только 1.Форма этого уравнения такова (пкс) грех (РХ)= +(НХ), потому что(РХ） ctgOrX)=+ -!£. (к） На рисунке 1-6 показаны обе кривые. Это трансцендентальное уравнение содержит бесконечное множество дискретных корней(8;, 3₂, 8…Есть и такие).Они просто лгут. В таблице через интервалы, где значение не включено. 

Два человека Значение конкретного интеграла ограничено тем фактом, что значения m и n больше не могут последовательно проходить через последовательность чисел. Специфический дискретный Напротив, значения C и O по-прежнему полностью произвольны. Ниже приведены уравнения, которые определяют различные распределения температуры бесконечно. Таблица 2 Корень уравнения При этом каждое соответствующее дифференциальное уравнение удовлетворяет граничному условию Неопределенность решения, которая существует из-за семантики значений C и D, устраняется начальными условиями. е. определение и согласованность с временными граничными условиями.

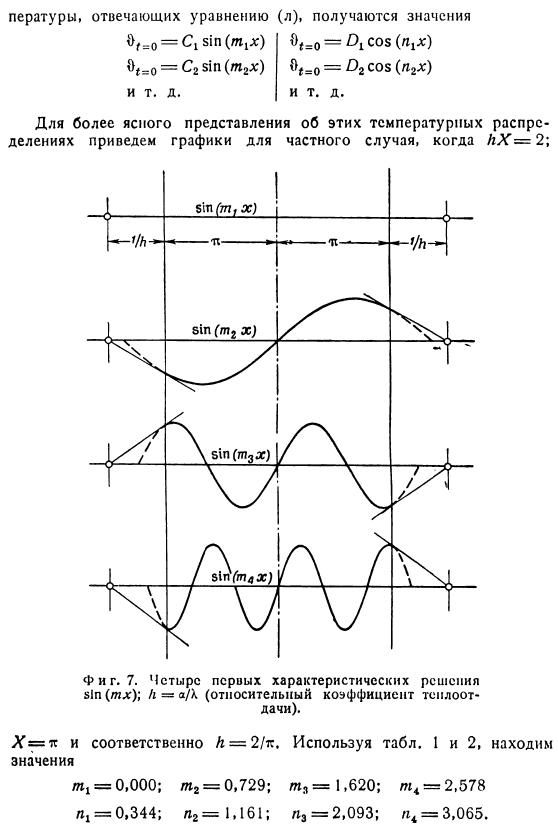
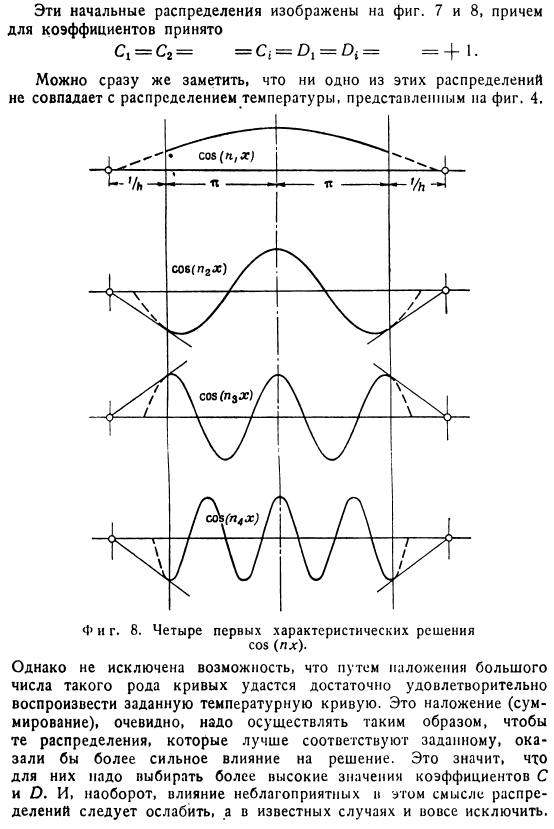
Если присвоить нулевое значение t выражению (l), то экзогенная функция будет равна 1、 Начальное распределение Получаем температуру, значение которой соответствует формуле (l ） Чтобы получить более четкое представление об этих распределениях температуры X = n, следовательно A = 2 / K. используйте таблицу. 1 и 2, найти значение 。 Эти начальные распределения показаны на фиг. 図３に示す。Кроме того, для коэффициентов 7 и 8 。 Вы можете сразу заметить, что ни одно из этих распределений не согласуется с распределением температуры, показанным на рисунке 1. 4. Однако, применяя множество таких кривых, можно достаточно точно воспроизвести заданную температурную кривую.

Это наложение (Резюме), очевидно, должно быть сделано таким образом, чтобы распределение, которое лучше соответствует данному распределению, оказывало сильное влияние на solution. It значит В их случае необходимо выбирать более высокие значения коэффициентов С и D. И наоборот, влияние неблагоприятного распределения в этом смысле должно быть ослаблено, если известно Вы можете исключить следующее: Очевидно, что в этих случаях вы должны выбрать очень малое или нулевое значение для C и O.

Для читателя достаточно принять, что пока такое решение о коэффициенте принимается по выбору. Если вы действительно можете это сделать, следующая формула справедлива: 。 В этом случае в любое последующее время, согласно формуле (l)、 Это уравнение является предпочтительным решением проблемы. Для повышения полноты, если индивидуальное распределение (k) удовлетворяет дифференциальному уравнению и граничным условиям, то сумма также должна быть доказана. Встречайте же conditions. In другими словами, необходимо обосновать, что общее решение может состоять из конкретного решения. Такие основания легко создать.

Для этого Необходимо сделать соответствующий дифференциал уравнения (n) и подставить полученные дифференциальные значения в уравнение (a) и соответственно © и (d).Возможность Построение общего решения из частного решения основано на том, что и основное дифференциальное уравнение, и уравнения граничных условий линейны、 Однородное уравнение. e. анализ решения. Уравнение (n) однозначно определяет температуру как функцию координат и времени, и эта функция берется как сумма 2 бесконечностей. Линия. Каждый член этих рядов является произведением постоянных, экспоненциальных и тригонометрических функций. Диапазон значений функций синуса и Косинуса равен-+ I–I.

Абсолютное значение экспоненты увеличивается, экспонента непрерывно уменьшается от I до O、 Поэтому он всегда меньше 1. Числа C и O таковы, что сходятся даже ряды уравнений (m), которые еще не содержат экспоненциальной функции. Это непосредственно следует из того факта, что функция 9ₜₗ₀= F (X) конечна на всем интервале. Добавление экспоненциальной функции значительно увеличивает сходимость ряда следующим образом: Из следующих рассуждений. В соответствии с Табуляция. В 1 и 2 значения m и n увеличиваются по мере того, как i увеличивается почти в арифметике series. So, в константах a и t индексы-m \ a1 и-n? Он будет увеличиваться. Геометрический progression.

В результате, поскольку порядковый номер I членов в ряду увеличивается, экспонента очень быстра и+ r равно zero. In другими словами, ее члены、 Она исчезает, что является factor. In в этом отношении экспоненциальная функция обычно называется коэффициентом сходимости ряда. чем больше значение t, тем больше эффект сходимости factor. So для очень большого t каждый из обоих рядов сводится к своему первому члену. Теперь мы можем уточнить значение уравнения (n). Любое начальное распределение температуры можно рассматривать как результат большого числа простых и сложных периодических температурных суперпозиций Распределение. Все эти распределения температуры имеют тенденцию быть flat.

Кроме того, в конце процесса более сложное распределение исчезает быстрее всего、 Простое распределение имеет приоритет. На примере этой задачи был обозначен путь, который привел бы к цели изучения стольких проблем теории теплопроводности. Но все исследование было полностью подчиненным. Конкретная рассматриваемая проблема, следовательно, существует gap. In в некоторых случаях я использовал довольно тривиальную вещь, чтобы избежать неотъемлемо важного математического анализа Физическое выражение. До тех пор, пока это соответствует целям настоящего документа, такие недостатки должны быть устранены путем рассмотрения аналитических методов на более общих основаниях.

Смотрите также:

• Методические указания по теплотехнике

Вывод дифференциального уравнения Фурье	Об отыскании частных решений
Краевые условия	О согласовании с условиями на поверхности