Оглавление:






Коэффициенты трения, тепло- и массопередачи при больших скоростях массообмена. Теория проницания
- В данном разделе анализируется зависимость трения, теплоты и массопереноса от скорости массопереноса в рамках теории osmosis. It основан на модели потока. Предположим плоскую форму профиля скорости вблизи межфазной границы. Таким образом, теория осмоса может быть применена в основном к жидкой фазе жидкостно-газовых систем (например, на рисунке 16-9 и 16-10). Впервые эта теория была использована при анализе массообменных процессов, проводимых в промышленных установках [14]. Более поздняя литература. Появились различные версии теории осмоса. Подробный анализ желательно проводить на примере системы. Профиль скорости плоской формы.
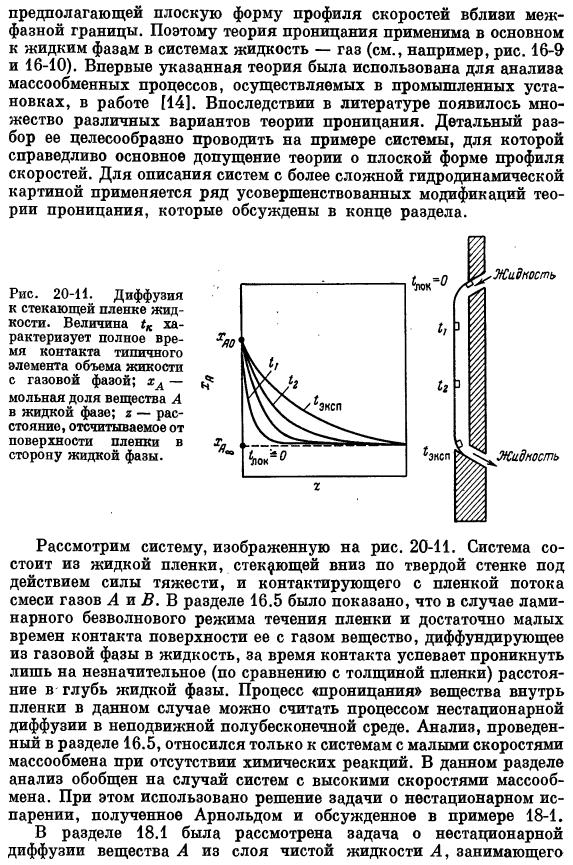
Несколько улучшенных модификаций теории проникновения используются для иллюстрации системы с более сложными гидродинамическими диаграммами. Конец раздела. Рассмотрим систему, показанную на рисунке. 20-11.Система состоит из жидкой пленки, которая протекает через твердую стенку под действием силы тяжести, и потока, который контактирует с пленкой Смесь газов а и В. Раздел 16.5 показал, что в случае свободной от волн области ламинарного течения мембранного потока время контакта его поверхности с газом достаточно мало. Диффундирует в жидкость из газовой фазы и за время контакта проникает только вглубь (по сравнению с толщиной пленки), незначительно углубляя жидкую фазу.
Обозначим разность между этой величиной и температурой среды вне йограничного слоя через Разность между температурой в любой точке пограничного слоя и температурой среды вне пограничного слоя обозначены через г. Людмила Фирмаль
Процесс В этом случае «проникновение» вещества в пленку можно рассматривать как процесс нестационарной диффузии на неподвижном полу в бесконечной среде. Анализ, проведенный в разделе 16.5、 Он применяется только для систем без химических реакций и с низкой скоростью массообмена transfer. In в данном разделе Анализ обобщен на случай систем с высокой скоростью массопереноса. Арнольд получил и использовал решение задачи нестационарного испарения, описанной в Примере 18-1.
В разделе 18.1 рассматривается задача нестационарной диффузии вещества а из слоя чистой жидкости а, занятого Преобразует полупространство z 0 в стационарную полубесконечную газовую среду z> 0, состоящую из чистого газа B, который нерастворим в жидкости A. та же задача、 Если отношение расхода NAININBₐ фиксировано, и обе начальные фазы содержат следующее, то в общем случае пересечения границы раздела одновременно используются 2 вещества (А и в). Субстанция А. следовательно, я-субстанция B. As начальная задача, ищем решение этой задачи для области z> 0 (либо жидкая, либо газовая фаза). Концентрация вещества а в нем постоянна и равна xAc.
Концентрация xa₀ на межфазной поверхности считается постоянной во всех точках t> 0.Окончательно、 физические свойства среды z> 0, такой как c и D’Ab, также постоянны. Формула мгновенной скорости массопереноса может быть получена неявно путем обобщения следующих уравнений: Где% — безразмерная скорость массопереноса, определяемая по формуле (18.13 а). Из Формулы (20.144)следует, что% остается постоянным даже во время диффузии. Это означает, что поток N АО и N во времени изменяется по закону. Распределение концентрации материала а в фазе z> 0 выражается формулой (18.16).Типичный профиль концентрации показан на рисунке.
Рассмотрим влияние ограничений При начальном содержании материала A в фазе z> 0 (xdso), уравнение (18.16), необходимо заменить безразмерную концентрацию X новой безразмерной переменной Chla. Соотношение Кроме того, безразмерные координаты Z = z (4£) dV 0′, введенные при рассмотрении примера 18-1, остаются неизменными. Уравнения (20.144)и (20.145) применимы к жидкой пленке, показанной на рисунке. 20-11.To для этого достаточно заменить эти выражения в качестве характеристик. Время t время ok. За это время каждый фиксирующий элемент поверхности движущейся сваи вступает в контакт с газом.
Когда поверхностная скорость vₘₐₓ постоянна А эффект волнообразования полностью отсутствует, 1L₀ K равно По x-состоянию, через которое проходит пленка, когда она стекает по стене, простая зависимость: tₙₒR = x / vₘ, ₓ. необходимо обратить внимание на стационарное решение, полученное заменой t на T.«, = xlvₘ». оно включает в себя элементы, ответственные за конвективный перенос веществ A и B.
- Однако ниже стенки молекулярная диффузия в этом направлении не рассматривается уравнениями (20.144) и (20.145). Предположение о важности вертикального вклада Как показывают численные оценки, диффузия оправдана для большинства участков движущейся пленки, за исключением очень узких областей вблизи точки x = 0. Формулы (20.144)и (20.145) вновь подчеркивают, что значения xAa и Nao / Nbo постоянны во всех точках межфазной поверхности и получены в предположении, что концентрация постоянна. xd o глубина жидкой пленки. Локальный коэффициент массопереноса K’x, lok, соответствующий любому фиксированному участку орошаемой стенки, определяется по формуле (20.2).
Здесь в качестве характеристической разности Axl была выбрана величина Ax = xAl-xAa₁.Где xAt-концентрация вещества в первом участке пленки. Подставляя выражение (20.147) в выражение (20.144), вы получаете: В случае ограничения малой скорости массопереноса уравнение (20.148) принимает следующий вид: Использование уравнений Если вы вычислите значение% (20.145), включенное здесь, это выглядит так: Этот результат идентичен исходному заключению Хигби[14], которое было сделано против диффузии при низких скоростях массопереноса.
В настоящем разделе будет решена простейшая задача, относящаяся к вертикальной плите Если такую плиту разогреть, то температура газа или жидкости близ ее поверхности будет повышаться и газ или жидкость начнут двигаться вверх. Людмила Фирмаль
Зависимость коэффициентов kx, lok от скорости массопереноса наиболее удобно анализировать с использованием тех же безразмерных Поправочные коэффициенты, ранее введенные при рассмотрении теории пленки: Соотношение потока Rab точно соответствует левой части формулы (20.144).Коэффициент скорости LV определяется по формуле (20.149) и (20.152) В= Х ^(20.154) Если формула (20.144) описывается переменными Rab и АВ, то расчет скорости массопереноса значительно упрощается. Многие расчеты удобно проводить с использованием понятия поправочного коэффициента 6AB = Vav / Rab. It равен следующим, согласно формулам (20.154) и (20.155).
Сравнивая выражения (20.155) и (20.156) с одной стороны, и выражения (20.117) и (20.122) с другой, можно легко убедиться, что интрузивная теория предсказывает больше Сильная зависимость коэффициента kJ, lok от скорости массопереноса, чем в теории пленок. Результаты этой теории и теории проникновения сравниваются количественно на рисунке. 20-13 и 20-14. Уравнения (20.155)и(20.156) могут быть использованы для описания процесса теплопередачи при условии, что величины X, p и Cp постоянны во всех точках жидкой фазы и одинаковы в обеих. Тип материала, который может быть transported.
Определяя коэффициенты Rt и t из соотношений (20.112) и (20.115), можно грубо рассмотреть эффекты рассогласования физических свойств. Легко увидеть Видно, что аналогом формулы для теплопередачи (20.150) является следующая формула: alok =₽&p / v * lok(20.157) Используя отношение (20.150), можно легко установить связь между значениями atk, xx и lok. Используя формулу (20.158), можно рассчитать коэффициент теплопередачи системы с низкой скоростью массопереноса. Опытная корреляция массообмена. Исходя из известного значения альковов, его можно рассчитать по формуле (20.155)-(20.156) или по графическим зависимостям, приведенным в разделе 20.7. Фиксированные шансы.
Турбулентный режим, уравнение теории передачи Жидкая фаза»старого» элемента, которая некоторое время находилась в контакте с газом, образует в пленке фигуру так называемого турбулентного перемешивания. В рамках таких выражений, значение 4L₀K продолжается Интерпретировать как»средний возраст»различных элементов поверхности、 Характеристики системы. Однако линейная зависимость определяется не молекулярным коэффициентом переноса, а (20.150). Усса. Между величиной kx и{Dab) между, при определенных условиях, подтверждается большим количеством данных по массопереносу. Глупый Жидкость Участок большого разнообразия жидкостных газовых систем, как найдено в химической технологии.
Сюда относятся, например, столбы, которые забиты плохо орошаемыми стенами колопна, своего рода пузырьковый слой(см. Пример 16-5).Следует подчеркнуть линейную зависимость коэффициента массопереноса от квадратного корня коэффициента Молекулярная диффузия теоретически эффективна только для систем, где профиль скорости в жидкой фазе считается почти плоским во всех точках области. Происходит диффузия. Для практически неоднородных профилей зависимость lock, kx от DAx различна(см.
Задачу растворения твердых стенок ламинарной пленки 16-10). Результаты теории осмоса также часто используются для описания процессов поглощения, которые осложняются химическими реакциями. Много примеров применения интрузивной теории к системе Он находится в монографии[1] с химической реакцией.\
Смотрите также:

