Оглавление:





Диффузия и химическая реакция внутри пористого катализатора. «Фактор эффективности»
- До сих пор диффузия газов и жидкостей анализировалась в системе простых форм. В этом разделе описывается, как составить материальный баланс основного объема и Первый закон Фика для описания диффузии внутри гранул пористого материала catalyst. It не пытается охарактеризовать диффузию в извилистых каналах материи. Вместо этого эффективный коэффициент диффузии используется для описания «средней» диффузии химически однородных веществ. В частности, рассматриваются сферические пористые частицы катализатора радиуса R (рис. 16-10). Частицы находятся в каталитическом реакторе и окружены газовым потоком, содержащим реагент а и продукт В.
Предположим, что концентрация вблизи поверхности конкретной частицы катализатора равна числу молей вещества а на единицу объема. Вещество а диффундирует в катализатор через извилистый канал и изменяется на вещество в на его поверхности (рис.16-11). 1. материальный баланс материала а Толстого DD глобулярного слоя на внутренней стороне частиц катализатора. Нар \ Р — ^ — нар | г + ДГ (г + ДГ) «+ Ял•4lg » ДГ = 0 Где LHLr | — число молей A, проходящих через виртуальную сферу на расстоянии r от центра сферы в направлении координаты r. члены уравнения, характеризующего Rx-4nr2Ar (16.84) Для образования вещества число молей обозначается числом а, а толщина — Дг в результате химической реакции.
Перенос тепла у периферии цилиндра с осью, перпендикулярной направлению потока, может быть вычислен, если опять-таки пренебречь уменьшением скорости внутри пограничного слоя потока. Людмила Фирмаль
Вычленить все члены уравнения баланса массы DG — * 0, это выглядит так: (16.86) Очевидно, что если рассматривать твердую фазу не как однородную среду, а как скопление гранул катализатора, то переход к такому пределу Это не согласуется с физической ситуацией явления. Поэтому в уравнении (16.86) символы NAᵣ и RA не должны интерпретироваться как величины, характеризующие условия в определенный момент времени. Скорее, следует предположить, что это значения, усредненные в пределах небольшой площади вблизи рассматриваемой точки-небольшие по сравнению со значением R, но большие по сравнению с размером. Канал внутри частиц катализатора.
Из следующей формулы найдите «эффективный коэффициент диффузии» вещества а в пористой среде. (16.87) Где са-концентрация газа а, содержащегося в порах. Эффективный коэффициент диффузии должен быть измерен экспериментально. Обычно его значение зависит от давления и температуры、 Структура пор катализатора аналогична. Действительно, механизм Диффузия 1 > размер поры мал и сложен Средний свободный путь диффузионной молекулы. Я не. Здесь мы подробно опишем механизм диффузии, но примем лишь то, что формула (16.87) может полностью объяснить этот процесс.
- Если вышеприведенную формулу заменить постоянным коэффициентом диффузии в Формуле (16.86), то она выглядит так: (16.88). Далее мы рассмотрим условия, при которых вещество А входит в организм. Ведутся первичные химические реакции. Поверхность Обмотка каталитических каналов. пусть a-доступная поверхность катализатора на единицу объема (твердое тело+пустота). таким образом, Ra = — k ^ asl, и уравнение(16.88) связано Это уравнение должно быть решено с граничными условиями. C Cas для a-r = R. Ca принимает конечное значение при r = 0.Дифференциальные уравнения, в которых появляется оператор (l / r2) (d / dr) [g2 (d / dr)), обычно обозначаются c / cA,= f ® / R.
Уравнение f можно записать в виде: ) ’ Общее решение уравнения (16.90), содержащее 2 интегральные константы, выглядит следующим образом: (16.90) (16.91) С использованием граничных условий, то еа(Г_ \ vBy ^ а / тряпка » Са> \ Р ’ЧД] /’ к ’ в / дар (16.92) При изучении химической кинетики и катализа их часто интересуют молярные потоки Na $или поверхностные молярные потоки r = R: Cai Ч (^,= 4nA2 ^ = — 4nna22)н-а(16.93) Используя формулу (16.92), вы можете видеть, что: Эта формула показывает скорость превращения (моль-с⁻*) вещества а в вещество в на другой частице катализатора радиуса R в зависимости от параметров рассматриваемого диффузионного процесса.
Соответственно следует ожидать, что температурное поле в пограничном слое может быть вычислено с хорошим приближением, если скорость в слое вплоть до поверхности пластины считать равной скорости потока. Людмила Фирмаль
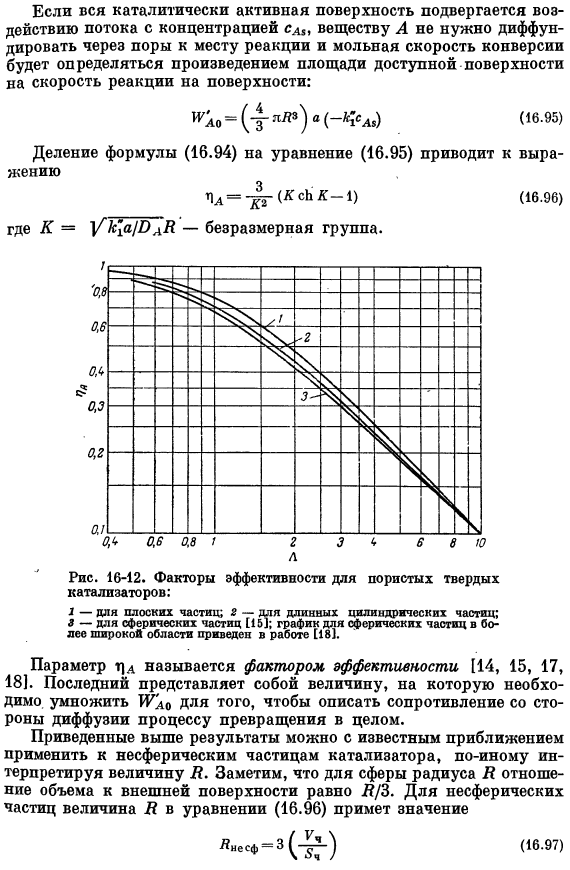
Когда вся каталитическая активная поверхность подвергается воздействию концентрированного потока Cd, вещество а не должно диффундировать через поры к месту реакции, и молярная скорость конверсии определяется произведением площади поверхности, доступной скоростью реакции поверхности Деление выражения на выражение (16.94) (16.94) является выражением 1С = — ^- (К ЛК-1) (16.96) Где K =VkᵢₐIDAR-безразмерная группа. Пористые твердые тела Этот параметр называется коэффициентом полезного действия[14、15、17、18]。Последнее-это значение, которое должно быть умножено на RYlo, чтобы представить сопротивление стороны распространения всему процессу преобразования.
Приведенные выше результаты позволяют интерпретировать значение R по-разному, чтобы применить известное приближение к несферическим частицам катализатора. Заметим, что для сферы с радиусом R отношение объема к внешней поверхности равно R / 3 для несферических частиц значение R в Формуле (16.96) принимает следующие значения: (16.97) Где U и S-объем и внешняя поверхность другой части катализатора. Коэффициент конверсии примерно таков: Куда? (16.98) В дальнейшем PL = — ZD2〜(для Cth PL-1) (£16.99)) А. = Ык а / да(V₄/ с^). Конкретные преимущества применения количества а очевидны из диаграммы. 16-12.
Если точное теоретическое выражение e (m) построить в виде функции A, то легко увидеть, что кривая имеет общую асимптоту для больших и малых значений A и не отличается существенно друг от друга в промежуточных значениях L. рисунок 16-12 подтверждает, что формула (16.99) правильно применима к определению несферических частиц.
Смотрите также:

