Оглавление:




Истечение газа из резервуара через сужающееся сопло. Формула Сен-Венана-Ванцеля
Истечение газа из резервуара через сужающееся сопло. Формула Сен-Венана-Ванцеля. Рассмотрим истечение газа из резервуара через узкое сопло(рис. 11.3).Размеры резервуара считаются очень большими по сравнению с размером отверстия, поэтому скорость жидкости в резервуаре можно считать равной нулю. Если конфигурация сопла выбрана правильно, распределение скорости на выходе из сопла будет приблизительно равномерным. Значения параметров газа в баке равны p0, p0 и T0.Они явно становятся тормозными параметрами. Давление во внешней среде и на выходе из сопла указано в px, а параметры газа в разделе 1-1 приведены в um, px, Tg, а площадь выхода из сопла проходит через 5. И затем… П°_ / Рэ _(Р \ \ Т ПГ \ РХ / \ По / Выражения(11.23) и (11.27)、 Или рассмотрим формулы (11.23) и (11.27)、 Последняя формула является модификацией формулы * Сен-Венана-Ванцеля о потоке газа. Определите массовый расход газа через сопло.
Адемар Жайе Клод валеду-Сен-вэн (1797-1886) выдающийся французский ученый в области машинистов и инженеров, член Парижской Академии наук. Людмила Фирмаль
- Исследования по гидродинамике Сэй-Венана посвящены общим уравнениям сопротивления течению труб и каналов, гравитационным волнам, установившемуся и нестационарному движению открытых каналов, газовыделению и вязким жидкостям. Очевидно, что при постоянных p0 и p0 массовый расход изменяется так же, как и функция f (e).Эта функция исчезает с * * 0 и I = I, поэтому между этими точками существуют экстремальные значения. Найти значение e / #(e)= 0, называемое критическим. После нормального преобразования, get. In в некоторых случаях k = 1.4 e » = 0.528.It легко видеть, что найденный экстремум является максимумом. Таким образом, максимальная или критическая масса flow.
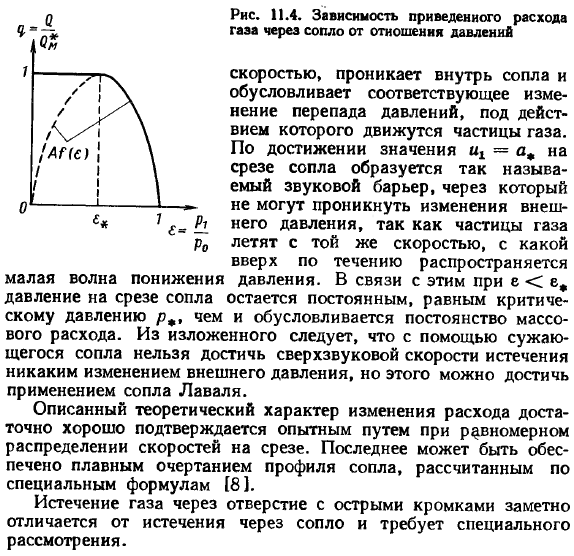
- By понимая соотношение любого расхода и его критического значения С2, удобно ввести уменьшение расхода С. из формул (11.48) и (11.50) видно: уравнение (11.38) используется для представления падения расхода, вызванного падением скорости. зависимость приведенного расхода q (e) от отношения давлений e = pg / p0 четко и качественно совпадает с зависимостью f(a) (рис.11.4).Тем не менее, в 0 е е области, эта зависимость физически не реально. Это происходит потому, что поток уменьшается по мере увеличения внешнего давления px decreases. In дело в том, что из опыта фактическая зависимость 9 © следует практически из теории только в диапазоне Е, Е 1, а для е е *массовый расход остается постоянным (равным 22 (7-1)). Рис. 11.4 физическая фактическая кривая 7 (e) показана в виде твердого тела line. To найдите причину такого характера этой кривой, установите расход газа, чтобы достичь на выходе из сопла максимального расхода.
Подставляя Формулу Е формулы (11.49) в правую часть формулы (11.47), можно увидеть, что расход при x = a, то есть максимальный расход, равен скорости звука. В этом заключается причина приведенных выше характеристик зависимости 7 (е). когда давление pg уменьшается в диапазоне E1, расход естественно increases. In При достижении значения= a *на выходе из сопла образуется так называемый звуковой барьер. Это связано с тем, что частицы газа летят с той же скоростью, что и небольшие волны декомпрессии, распространяющиеся вверх по течению, поэтому изменение внешнего давления не может проникнуть through.
Кроме того, небольшое изменение внешнего давления, распространяющееся со скоростью звука, проникает через сопло и под влиянием движения частиц газа вызывает соответствующее изменение перепада давления. Людмила Фирмаль
- In в связи с этим в ээ» давление на выходе из сопла поддерживается постоянным и равно критическому давлению/**.оно определяет постоянство массового расхода. Из вышеизложенного следует, что использование конусного сопла делает невозможным достижение сверхзвукового расхода за счет изменения внешнего давления, что может быть достигнуто с помощью сопла Лаваля. Описанный теоретический характер изменения расхода очень хорошо подтверждается экспериментально при равномерном распределении скорости на резании. Последнее обеспечивается плавными контурами профиля сопла, рассчитанными по специальной формуле[8]. Отток газов из острого отверстия существенно отличается от оттока из сопла и требует особого ухода.
Смотрите также:
Возможно эти страницы вам будут полезны:

