Оглавление:
Гидравлический расчет трубопроводной системы
Второе граничное условие заменяется условием u (y, t) = 0 при y → . (6, 121) Кроме того, у нас есть начальное условие u (y, t) = 0 для t ≤ 0. (6, 122) 6. 2 Нестационарные однонаправленные потоки 187 Уравнение (6. 119) является линейным уравнением курсовой работы по гидромеханике, и поскольку u входит в задачу только линейно из граничного условия (6. 120) поле u (y, t) должно быть пропорционально u, так что решение должно иметь вид u / u = f (y, t, ν). (6, 123)
- Поскольку функция слева безразмерна, f также должна быть безразмерный, что возможно только в том случае, если аргумент функции mensionless.
- Однако единственная линейно независимая безразмерная величина это комбинация y2 / (νt). Weset = 1 2 y √ νt (6, 124) и теперь имеем дело с переменной подобия η, потому что решение не может изменить, если разветвленного трубопровода y и t изменяются так, что η остается постоянным.
Вместо (6. 123) мы сейчас пишем u / u = f (η), (6, 125) и из (6. 119) получаем обыкновенное дифференциальное уравнение −2 ηf = f (6. 126) с f = df / dη. Двойная интеграция дает общее решение f = c1 η 0 e − η2 dη + c2. (6, 127) Для y = 0 имеем η = 0, и граничное условие (6. 120) становится f (0) = 1, (6, 128) и поэтому следует, что c2 = 1. Если мы подчиняем (6. 127) с c2 = 1 к «Граничное условие» (6. 121), 1 / c1 = — 0 e − η2 dη (6. 129) должен держать.
Несобственный интеграл имеет значение 21 √π, и поэтому c1 = −2 / √ π; (6, 130) таким образом,
решение гласит u / u = 1-2 √ π η 0 e − η2 dη при t ≥ 0. (6, 131) 188 6 ламинарных однонаправленных потоков Интеграл эрф (η) = 2 / √ π η 0 e − η2 dη (6. 132) является системы с ответвлениями функцией ошибки. Fort = 0, мы имеем η → и u / u = 0; Таким образом, начальный состояние удовлетворительное. 6. 3. Однонаправленные потоки неньютоновских жидкостей 6. 3. 1
Постоянный поток через круглую трубу Чтобы вычислить поток неньютоновских жидкостей, мы вернемся к Уравнения Коши.
Как и в случае ньютоновских жидкостей, для кинематической сыновья единственная неисчезающая составляющая скорости — это то, что в осевом направлении и это зависит. Людмила Фирмаль
Поэтому мы имеем дело с однонаправленным течение, а тензор напряжений имеет вид (3. 35) в цилиндрических координатах, где индекс 1 соответствует направлению z, индекс 2 — направлению r и индекс 3 в направлении ϕ. Так как тензорная функция ϕij в (3. 35) соответствует тензору напряжений трения
pij (который зависит только от γ˙ = du / dr, то есть onr), запишем тензор напряжений в следующей матрице форма.
Примеры решения с методическими указаниями
| Решение | Лекции |
| курсовая | Учебник |
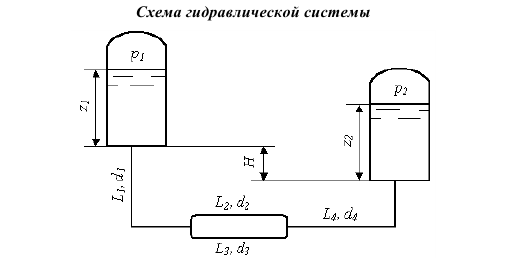
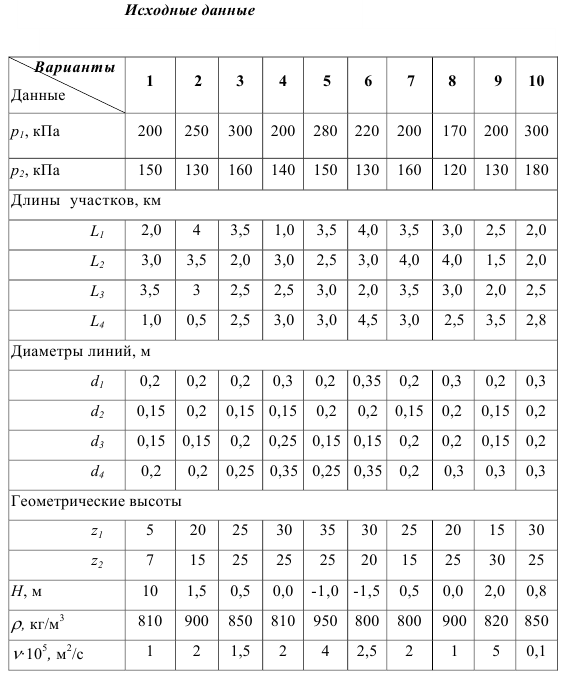
Содержание работы 1. Теоретическая часть. Теоретические основы гидравлического расчета сложных трубопроводов. 2. Расчетная часть. Разность отметок между днищами резервуаров h. Резервуары соединены трубами, из которых вторая и третья проложены параллельно. Труба 3 имеет задвижку.
Трубы стальные бесшовные новые. 1) Определить расход нефти в трубах, проложенных между резервуарами, имеющими давление p1 и p2 и уровни нефти в них z1 и z2. 2) Определить расходы в трубах. 3) Как изменятся эти расходы, если закрыть задвижку? 4) Повторить расчеты по пунктам 1, 2, если в трубах образуются значительные отложения. 5) Оценить, в каких пределах (в процентах) изменится расход в системе по пункту 1, если уровни в резервуарах станут одинаковыми. Схема гидравлической системы
