Оглавление:
Гидравлический расчет сложного разветвленного трубопровода
Обратите внимание, что h2 / ν — типичное время для диффузии вращения через высота канала h. В первом случае это время намного меньше, чем типичное время колебаний 1 / ω. Процесс диффузии регулируется в каждый момент курсовой работы по гидромеханике поле скоростей к постоянному потоку сдвига с мгновенной стенкой скорость uw (t). Это то, что называется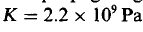
квазистационарным течением.
- Используя первый член разложения гиперболической функции синуса для небольшие аргументы у нас есть u = uˆ eiωt ωh2 / 2ν (1 + i) (1 — год / ч) ωh2 / 2ν (1 + i) , (6. 115) и сделать вывод, что u = uˆ cos (ωt) (1− y / h) = u (1 — y / h). (6, 116)
- Уравнение (6. 116) соответствует (6. 4), где верхняя пластина представляет нагнетательной линии движущаяся стена.
- Мы также получаем этот предельный случай, если кинематическая вязкость ν стремится к бесконечности.
Как видно из (6. 103), нестационарный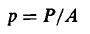
член исчезает. Этот предельный случай ν → для фиксированного η также соответствует принятию предела → 0, таким образом, игнорируя инерционные члены, и, следовательно, попадает в группу б) классификация обсуждается в разд. 4. 4. В пределе ωh2 / ν 1 используется асимптотическая форма гиперболического синуса Функционирование и запись (6. 112) в виде u = uˆ e- √ ω / 2νyei (ωt- √ ω / 2νy) , (6. 117) или же u = uˆ e- √ ω / 2νy cos (ωt — ω / 2νy). (6, 118) Разделение h больше не появляется в (6. 118).
Измеряется трубопроводные системы в единицах λ = 2ν / ω верхняя стена находится в бесконечности.
Относительно переменной y решения также имеют форма волны; мы называем эти поперечные волны длиной волны λ 186 6 ламинарных однонаправленных потоков. Людмила Фирмаль
Распределение скорости над колеблющейся стеной 6. 2. 2 Поток из-за стены, которая внезапно приводится в движение Используя (6. 118), мы могли бы в принципе сформировать решение для стены, которая внезапно ускоряется до скорости u. Однако более поучительно взять другой путь, который начинается непосредственно с дифференциального уравнения в частных производных ∂u ∂t = ν ∂2u ∂y2. (6, 119)
Это дифференциальное уравнение также описывает нестационарное одномерное тепло проводимости (где ν затем заменяется коэффициентом теплопроводности а), и поэтому желаемое решение также появляется в проблемах теплопроводности. Отсутствие скольжения на стенах.
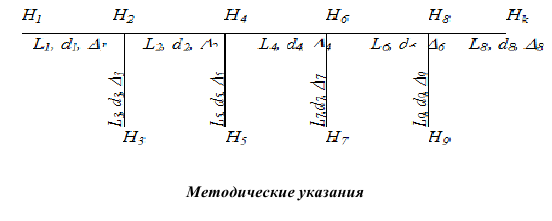
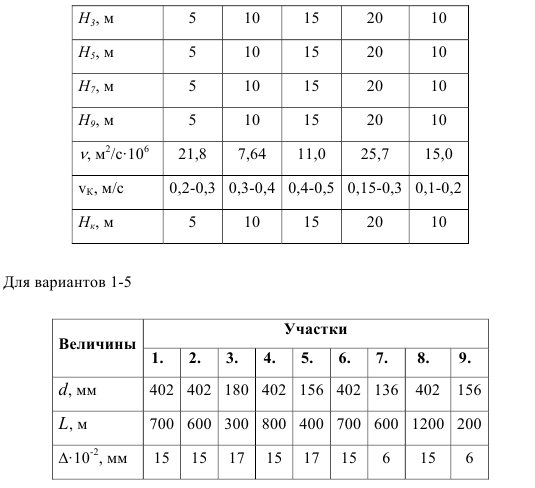
Содержание работы 1. Теоретическая часть. Принципы гидравлического расчета сложных трубопроводов. Расчет трубопроводов, соединенных последовательно и параллельно. 2. Расчетная часть. Заданы напоры в конечных пунктах разветвленной водопроводной сети (в пунктах потребления), линейные размеры трубопровода (диаметры участков, их длины и шероховатости труб). Известна также скорость течения в конечном пункте потребления.
Схема трубопровода приведена на рисунке. Вязкость жидкости считается известной и постоянной по всей длине трубопровода. Все исходные данные приведены в таблице. 1) Определить напоры h2, h4, h6 и h8 в узловых точках и начальный напор h1. 2) Найти расходы и скорости течения на всех участках разветвленного трубопровода. 3) Рассчитать изменение всех искомых параметров при изменении скорости vК в конечном пункте потребления. 4) Построить характеристику трубопровода Н = Н (q). Схема трубопровода
