Оглавление:







Определение концентраций, скоростей и массовых потоков
- В многокомпонентных системах концентрации компонентов могут быть представлены различными способами. Здесь мы ограничиваемся 4 методами. Объемная массовая концентрация p: — масса компонента i Раствор pa единичный объем; объемная молярная концентрация Ci — количество молей компонента g на единицу объема раствора. Массовая доля a>₁= pf / p-это объемная массовая концентрация компонента g, деленная на общую массовую плотность раствора. Молярная доля X / = cjc-объемная молярная концентрация компонента g, деленная на общую молярную плотность раствора. (Слово «раствор» означает смесь однофазных газов, жидкостей или твердых веществ.)В таблице.
Представлен обзор единиц концентрации и взаимосвязи между различными способами их представления в двоичной системе счисления. В смесях, в которых протекает диффузионный процесс, химически однородные отдельные компоненты движутся с разной скоростью. указывает скорость Z-го компонента относительно th Фиксированные оси*.Затем, когда компонент h смешивается, локальная массовая средняя скорость v может быть описана следующим образом: 5— — (15-1) Серебро pv-это локальная скорость, через которую определенное количество массы проходит через единицу сечения, расположенную перпендикулярно направлению скорости o.
Во-первых, как было показано теоретически Максвеллом и экспериментально Кундтом и Варбургом, вблизи границы скорость потока не равна нулю и поток скользит вдоль стенки с конечной скоростью. Людмила Фирмаль
Это локальная скорость, которая может быть измерена с помощью трубки Пито и соответствует символу o, который использовался в предыдущей главе для обозначения чистой жидкости. Аналогично, вы можете найти «локальную среднюю молярную скорость». ⁷ (15.2) заметим, что значение co * — это локальная скорость, через которую соответствующее число молей проходит единица поперечного сечения, перпендикулярная направлению скорости o*. в будущем обе эти средние скорости будут широко использоваться в книгах. Можно также использовать другие средние скорости, например объемные средние скорости (см. задачу 15-11).
Если система движется, то часто приходится рассчитывать скорость заданного компонента с v или v *вместо скорости с фиксированными координатами. Это приводит к определению понятия «диффузионность». Скорость диффузии компонента I (15.3) ,- *=Коэффициент диффузии компонента: относительно v *(15.4) уравнения (15.3) и (15.4) указывают на движение компонента i относительно локального движения жидкости. Обзор характеристик скорости в бинарных системах и некоторые полезные связи между различными скоростями показаны в таблице. 15-2. Это важно для читателя, чтобы четко понять значение различных типов speed.
Рассмотрим конкретную систему и покажем ее действие на схеме (рис.15-1).Обсудите, что происходит б — Таблица 15-2.Двоичный расход потока в =(1 / п)(Rlл+ PBfB)=(ШдА+ -Средняя массовая скорость (Р> =(1 / с)(СЛа+ cbvb)> =(хА* а + ХВ * с)Средняя молярная скорость (г> Жидкость а испаряется и диффундирует в длинную трубку. Первый Много. Нажимаем пара B до. Однако, 15-1, а, ясно как следует из рисунка Не существует границы между чистым паром и чистым паром Б. Он движется. Вверх Б При смешивании 2 потоков пара (рис. 15-1, б) в любой точке колонны а он поднимается быстрее, чем общее среднее движение а и B. At в то же время, B спускается медленно из-за диффузии. На рис.
- Показан вектор скорости выполнения условий для xA = 1/6,= 12, vA- — V * = 3 и LGA = 5L / V. Читатель должен проверить вектор скорости при других условиях. Теперь, когда концентрация и скорость были исследованы, мы можем найти массовый расход и молярный расход. Массовый (или молярный) поток компонента i-это векторная величина, указывающая на массу Число молей компонента i, проходящих через единицу площади за единицу времени. Движение приписывается фиксированным координатам-локальной массовой средней скорости o или локальной молярной средней скорости v*.
Массовый и молярный расход до фиксированных координат определяются по следующей формуле: Массовый расход (15.5) Молярный расход НТ = ’ Иви (15.6) Массовая и молярная скорости приблизительно равны: массовый расход Молярный расход Расход по отношению к среднему значению массы второй = Пи (Ви-в) (15.7) Л = е / ( «/- » ) (15.8) Массовые и молярные скорости потока для молярной средней скорости o *описываются следующим образом: Массовый расход Л = П/(» ’/-» *)(15.9) Молярный расход 4 = 4(«»-«*)(15.10) Таблица определяет поток двоичной системы. 15.3 некоторые зависимости между различными потоками.
Так как скользящий поток по предположению представляет собой явление, относящееся к малым числам Кнудсена, то точное значение этого явления неизвестно, однако этот факт был успешно использован в полуэмпирическом анализе, чтобы согласовать экспериментальные данные по всему режиму потока от газовой динамики до свободного молекулярного потока. Людмила Фирмаль
Следует отметить, что определение массового расхода является неполным, если не указаны единица измерения и система отсчета. В математическом плане при решении задачи диффузии ни одна из вышеперечисленных 6 характеристик потока не эквивалентна, но каждая из них показывает некоторые преимущества при правильных условиях, и все они описаны в литературе. При вычислении процесса обычно желательно связать его с фиксированной системой координат по отношению к устройству, поэтому поток IV (и nf в меньшей степени) используется в инженерной практике. Поток J ₍ よ び J * используется для измерения скорости диффузии и полезен для создания уравнений обмена для многокомпонентных систем.
Потоки J и j ’ редко используются, но включены здесь для completeness. In кроме того, чаще всего используется моль потока IV. Пример 15-1.Какова связь между молярными потоками, а) потоками Р-компонентной системы, J, n, N? b) указывает, что общий поток J *равен нулю. Решение, а) сначала объедините уравнения (15.2) и(15.10).
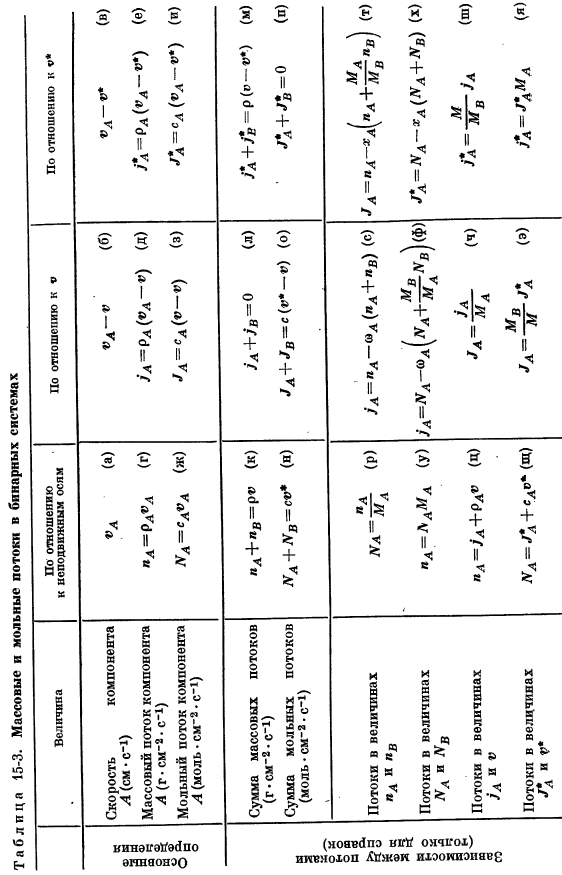
Таблица 15-3.Массовый расход и молярный расход бинарной системы На неподвижной оси по отношению к Весюшве Компонента скорости-(а) (б) — л — (б) Джа с (см * с-1) Массовый расход компонентовl = Rl *l (g)/ L = Rl (l -») (d) Ul-Rl^ -*) (f) 1 | л(г-см-2-с-1) Молярный поток компонента Na = ’a’ a(g)•FA = » A ( • — )») © * ^ = » A (2> A-2> -) (и) Общий массовый расход «l +» B =P(k) / l + / vi «(l) D + D = p ( » — » * ) (M) (г-см-2-с-1) Сумма молярных потоков JVA + JVB = M» *(n) JA + / B = c ( » * — — — ) (о) у* + ^ * =о(и) (моль * см-с-с-1) Я стока Лгл = ^ Л (Р)/ Л-«Л- „Л (- Л +“ С) (О)• Л = „Л -“ Л( „Л + Л ^“ С(Т) И затем ч Iototi-lushchinah „а = л / А(Г)) () гы =“ а-ха (а + с) ж У потока » л = / л +РЛ(ч) Джама (ч) А.
Смотрите также:

