Оглавление:





Ламинарное течение между соосными вращающимися цилиндрами
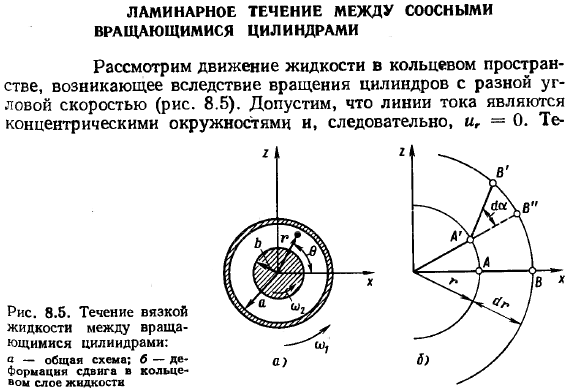
Ламинарное течение между соосными вращающимися цилиндрами. Рассмотрим движение жидкости в кольцевом пространстве, возникающее при вращении цилиндров с различными угловыми скоростями (рис.8.5).Предположим, что линия потока концентрична и в результате u = 0.ОдинПредположим, что расчет не учитывает влияния плоских (m = 0), стационарных (d / d (=-0)) и массовых сил. При этих начальных условиях системы уравнений движения(5.14) и (2.25) имеют вид Из последнего уравнения (уравнения неразрывности) видно, что скорость q = 0 не зависит от координатного угла 0.Однако из-за осевой симметрии потока давление p не зависит от этого variable. In кроме того, все производные по отношению к r будут равны нулю. Это происходит потому, что нет никакого движения в направлении этой оси. Таким образом, вы получите систему (8.14) 1 * от Ар__. 0Ri. 1 с Ли. p ag g’Y * t от -~~ ~ Второе из этих уравнений содержит только 1 необходимую функцию, которая может быть решена независимо от первого.
аким образом, мы находим закон распределения скоростей в кольцевом пространстве. Людмила Фирмаль
- Если% и B2-угловые скорости внешнего и внутреннего цилиндров, граничное условие скорости u-o для r-A. и-R = B co2r. Общее решение 2-го уравнения (8.14) может быть найдено, если скорость представлена функцией вида u-gk. Подставляя его в уравнение、 k (k-1) r * −2 + kgk-2-rk 2 = 0 или k7-1 = 0, то есть k =±1. Таким образом, частичным решением будут функции u-g и u-g-1, а их линейная комбинация будет общим решением. (8.15)) И-Ар + Б! г. Подставляя приведенные выше граничные условия в Формулу (8.15), находим систему, определяющую константы A и B. ТПрактический интерес в этом случае представляют прежде всего напряжения сдвига и создаваемые ими сила и момент трения. 298. Напомним, что для нахождения формулы напряжения сдвига, согласно формуле Ньютона, оно пропорционально угловой скорости сдвига(см. раздел 5.1).
- Цилиндрические грани радиусов r и r + yr отличаются от тонких слоев жидкости, подвергающихся сдвиговой деформации из-за разницы угловых скоростей 10 и 2. To будь ясен, о! а) 2.Предположим, что окружная скорость U и угловой скорости U в точке а(рис. 8.5, 6).Угловая скорость в точке B И равный/ g +, следовательно, в то же время Он расположен в точке B и проходит по дороге Если угловые скорости ω^и ω2 одинаковы, то слой жидкости между цилиндрами не подвергается сдвиговой деформации и вращается вокруг общей оси цилиндра. cylinder. In в этом случае отрезок y между временем W перемещается в положение A’b. But co. И U2, из-за разницы, перейти в положение A’b’. принимая r = a и r = b, найти значения касательных напряжений для внешнего и внутреннего цилиндров соответственно. Затем вычислите момент силы трения. Согласно формуле (8.18), поскольку m не зависит от координатного угла 0, искомый момент представляется формулой: = 5tg = 2gp1hg.
Двести девяносто девять Где I-размер цилиндра вдоль шины. 5-сторона цилиндра. Если вы примете во внимание (8.18), вы получите a^ 1 * Л 1 ОСН3、 А3-В2 ^ <sup class=»reg»>®</sup>2^ ’ Как видно из этой формулы, момент трения не зависит от радиуса слоя R. Это означает, что в случае 2 соосных цилиндрических плоскостей с жидким слоем в качестве границы величина распределенных на этих поверхностях вязких сил равна и знак равен opposite. In другими словами, они имеют баланс моментов вязкой силы. Рассмотрим особые случаи. 1.Неподвижный наружный цилиндр (o»!= 0), и 6 = A-b в небольшом количестве между цилиндрами. Далее, примерно до 5 марта Как видно из формул (8.19) и (8.20), момент и сила трения быстро возрастают с уменьшением зазора 8. Уравнения(8.19)и(8.20)были впервые использованы для расчета трения подшипника скольжения до тех пор, пока не была разработана более точная гидродинамическая теория смазки.
Николай Павлович Петров (1836-1920) выдающийся русский инженер и ученый, почетный член Петербургской Академии наук, проводил многочисленные исследования по гидродинамике вязких жидкостей, измерениям вязкости и создаваемым осям. Людмила Фирмаль
- Это уменьшает эксцентриситет положения вала в подшипнике. Основы этой теории будут рассмотрены ниже. Тем не менее, в 1883 году Н. П. формулы, предложенные Петровым *(8.19)и (8.20), остаются в силе и сегодня, так как многие механические конструкции используют вращение коаксиальных цилиндров. Вал подшипника на высокой скорости. 2.Вращение цилиндра в пределах неограниченной жидкости, т. е.©! = 0 и-ОО. Согласно (8.16), A = 0 и B = b2CO2. Распределение скорости по (8.15) описывается зависимостями у = b2sc / г, (8.21 Или следуйте закону u = sop $ 1.На поверхности она имеет цилиндрическую форму r = b и ipov = 6co2.Этот закон распределения скоростей 、 Гидродинамическая теория смазки. 300. Из раздела 7.2 известно, что одна плоскость идеальной жидкости является свойством потенциального течения в поле вихрей. Поэтому в случае движения рассматриваемой вязкой жидкости поле скоростей.
Смотрите также:
Возможно эти страницы вам будут полезны:
- Установившееся ламинарное течение между параллельными плоскостями.
- Постановка общей задачи о ламинарном установившемся течении в цилиндрических и призматических трубах. Течение в кольцевой трубе.
- Диффузия вихрей в вязкой жидкости.
- Приближенные уравнения для малых чисел Рейнольдса. Плоские ползущие течения.

