Оглавление:



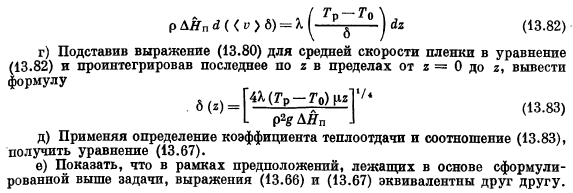

Межфазный перенос в неизотермических системах. Задачи
- При фиксированном поперечном сечении с трубами температура внутренней поверхности стенки составляет 71,1°С, а объемная температура жидкости в этом сечении-15,56°C. На этом участке мы определяем локальный тепловой поток стенки трубы, предполагая, что локальный коэффициент теплопередачи уже достиг некоторого асимптотического значения. Ответ:= — 1,7-10 ккал-м ^ — ч » 1. 13-2. Теплопередача от конденсационного пара, а)на наружной поверхности вертикальной трубы с наружным диаметром 2,54 см и длиной 30,5 см поддерживается постоянная температура 87,8°С. Какова суммарная скорость теплопередачи через стенки трубы, если она окружена насыщенным паром под давлением 1 атм?
Каков коэффициент теплопередачи, если труба расположена горизонтально в тех же условиях? Ответ: а)2117 ккал-ч ’1; б) 3024 ккал-ч» 1. 13-3.Передача тепла от одной сферы в условиях вынужденной конвекции. Твердая сферическая оболочка с внутренним диаметром 2,54 см помещается в однородный воздушный поток, движущийся со скоростью 30,48 м * с-1 при давлении 1 атм и температуре 37,8°с. благодаря электрической спирали, встроенной в оболочку, температура поддерживается на уровне 93,3°С. Как насчет скорости нагрева спирали (cal-s «1»), чтобы соблюдались указанные условия? Не принимайте во внимание радиацию. Ответ: 3.35 cal-s » 1.
Некоторые предпринятые попытки слишком громоздки, чтобы их можно было поместить в текст дан- ного объема, но нужно сделать некоторые замечания по существу. Людмила Фирмаль
Передача тепла от одной сферы при условии естественной конвекции. Сферическая оболочка с радиусом 2,54 см внутри расположена в неподвижном воздухе atmosphere. As описанная в предыдущей задаче поверхность оболочки поддерживает постоянную температуру 93,3 RS. Если температура воздуха составляет 37,8 RS, а давление-Атмосферное давление, то найти электрический нагрев в устойчивом состоянии? Не принимайте во внимание радиацию. Ответ: 0.332 cal » s » 1. 13-5.Ограниченное локальное число нуссельта для ламинарного течения в трубе и постоянного теплового потока к стенке.
Уравнение (9.172) показывает асимптотическое распределение температуры жидкости (константы p, p, Cp и l), движущейся вдоль длинной трубы с постоянным тепловым потоком к стенке. Это распределение используется для указания того, что соответствующее число нуссельта равно 4 / c. 13-6.Измеритель скорости горячего воздуха[2]. анемометр представляет собой тонкую проволоку, обычно изготовленную из платины, и при помещении в газовый поток нагревается электрическим током. Температура провода, которая является функцией температуры газа, расхода и скорости нагрева провода, может быть найдена путем измерения электрического сопротивления.
Поместите прямую цилиндрическую проволоку диаметром 0,25 мм и длиной 1,27 см в воздушный поток, движущийся со скоростью 30,5 м / с. Температура воздуха составляет 21°C. Как должна быть скорость подачи энергии (Вт) к проводу, чтобы температура поверхности всегда поддерживалась постоянной и была равна 316 RS? Действие теплового излучения и теплопроводности вдоль провода не учитывается. Б) для каждого конкретного газа и проволочного материала при определенном значении температуры(и, следовательно, при определенном сопротивлении) теоретически была установлена следующая зависимость[32]. Здесь 1-сила тока, необходимая для поддержания заданной температуры на поверхности провода.
- Скорость газа от провода. Рисунок (13.74) согласуется с корреляцией, показанной на рисунке. Для систем, описанных в пункте 13-9,»а», расход газа составляет 30,5-91,5 м » с-1?Что означает константа C в выражении диапазона (13.74)? 13-7.Применение метода размерного анализа. Рассмотрим систему, описанную в первой части раздела 13.2.In эта система, безразмерный профиль скорости[уравнение (6.44)] и температура[уравнение(13.27)] уже были получены методом размерного анализа. а) используйте приведенную выше формулу и определение»объемной»температуры T ^ g (см. Пример 13-1) для указания эффективности соотношения.
Используя формулу предыдущего результата и коэффициент теплопередачи, получим зависимость (13.30)-(13.32). 13-8. соотношение alok и a | P во многих конструкциях трубчатых теплообменников(см. Пример 14-2) температура Th поверхности каркаса изменяется пропорционально объемной температуре T Steam. In в этом случае очень простая связь может быть установлена между коэффициентами aLok и a | P. а) на основе отношений(13.5)、 SOCLOCO *(е)= -% dfgr АТБ (13.76)) И так оно и есть.、 (13.77)) (13.78) Г1. 1 У. / , » Цкч-ТТ ] Алок ЛГ-4 ПХЗ Д(Go_G.) 1Н о b) сочетание соотношений (13.4) и (13.77) для получения зависимостей a1n = = / арок^ О Где _ — общая длина всех труб.
Режим переходного потока лежит между скользящим потоком и свободномолекулярным потоком и характеризуется тем, что средний свободный пробег молекул имеет приблизительно ту же величину, что и характеристический размер тела. Людмила Фирмаль
Условия (длок. Если / Db) r = * 0″удовлетворяется, то из уравнения (13.78) получаем следующее простое соотношение: [Алок] 2 = Б = [В | П] 1.б + ^ — 13-9.Теплопотери труб обусловлены естественной конвекцией. Если температура поверхности трубы составляет 93,3°C, а температура воздуха-82,2 ° C, увеличиваются или уменьшаются потери тепла в системе, описанные в Примере 13-3? 13-10.Нуссельт формулировка коэффициента теплопередачи конденсации пара. Рассмотрим слоистую пленку конденсата, протекающую через вертикальную стенку(см. рис. 13-14), и предположим, что эта пленка имеет основное сопротивление теплопередаче от пара к стенке. wall.
Кроме того, мы предполагаем следующее: 1) сила трения между жидкостью и паром не сильно влияет на распределение скорости пленки. 2) характерные значения физических параметров пленки соответствуют температуре, равной среднему арифметическому температуры пара и охлаждающей поверхности, причем температуру последней можно считать постоянной. 3) инерционный член уравнения движения пленки пренебрежимо мал по сравнению с членом, описывающим действие гравитационных и вязких сил. 4) эффект изменения энтальпии внутри конденсатной мембраны незначителен по сравнению с эффектом переноса тепла конденсации. 5) тепловой поток во всех точках строго перпендикулярен поверхности стены.
В рамках этих предположений предлагается выполнить следующие действия: а) для средней скорости пленки определенной толщины б используйте формулу, полученную в разделе 2.2. Мы применяем эту формулу к пленке конденсата, считая, что она справедлива для любого значения координаты r. б) написать уравнение сохранения энергии в пленке и опустить в него члены, учитывающие влияние кривизны поверхности и вклад конвективного теплообмена. Тепловой поток, проходящий через пленку к охлаждаемой поверхности определяется следующим уравнением. Г-К — Кусать-* (13.80)) (13.81)) в)при сливе со стены пленка захватывает дополнительную порцию жидкости, которая образуется в процессе конденсации.
Последнее сопровождается выделением тепла. Выделение тепла — это количество на единицу массы вещества, подвергающегося фазовому переходу. п ДНП в(6) — х(-) 2(13.82)) d) подставляет формулу для средней скорости пленки (13.80) в Формулу (13.82), интегрируя последнюю через r в диапазоне от r = 0 до r и выводя формулу. * ( » ) = [ •/ » (13.83) д) получить уравнение (13.83), используя определение и соотношение коэффициента теплопередачи (13.67).
Смотрите также:

