Оглавление:







Определение коэффициента теплоотдачи
- Рассмотрим поток жидкости или газа, движущийся в канале, или жидкость, обтекающую твердый объект, погруженный в канал. Температура твердой поверхности, контактирующей с потоком, выше температуры движущейся среды, поэтому мы предполагаем, что тепло передается от поверхности к потоку. Коэффициент теплопередачи через границу раздела между твердой и жидкой (или газообразной) фазами, до первого приближения, представляет собой площадь границы раздела и разность температур между жидкостью (газом) и твердым телом, т. е. — =ОЛГ (13.1). Где O-количество тепла, поступающего в поток за единицу времени. A-характерная область. DG-это характерная разница температур.
Заметим, что коэффициент теплопередачи для каждой конкретной системы остается практически неопределенным до тех пор, пока не будут определены значения A и DT. Теперь давайте рассмотрим общепринятый способ найти значение a в 2 различных геометриях потока. В качестве примера течения в канале рассмотрим движение жидкости (или газа) по кольцевой трубе диаметром D (рис.13-1) (рис. 13-1).Имеется нагревательный участок длиной L стенки, и температура внутренней поверхности этого участка изменяется с расстоянием вдоль оси трубы.
Одним из первых успехов в кинетической теории газов было предсказание того удивительного факта, что динамическая вязкость и теплопроводность идеальных газов независимы от давления. Людмила Фирмаль
Значение а — это коэффициент пропорциональности, который называется коэффициентом теплопередачи. Если поток дал тепло твердой стенке, то очень очевидно, что можно использовать то же самое определение коэффициента теплопередачи. Соотношение(13.1) иногда называют «законом охлаждения Ньютона» (см. также 244 и^ 263).Однако на практике выражение (13.1) не отражает ни одного термина, поэтому такой термин не считается удачным. Хотя это физический закон, он действует только как свойство величины.
Средняя объемная температура 13-1.Передача тепла круглой трубки: 1-жидкость G, поступающая в трубу при объемной температуре Tg-участок трубы、 Объемная температура tjjv трубы-поперечное сечение шероховатое+дно Процентное содержание жидкости Th *в нагревательной секции трубы увеличивается от Tbᵢ секции I до Tb T секции II.
Существует 3 способа расчета коэффициента теплопередачи костей, заключенных в нагревательной секции трубы: Q =a₁ (nDL) (Tₙ-Tb₁) Вопрос-АА-ям.(Go1-П.) +(Гов-Ки) / ППС (go1-1’b1) — (Гоа-^ АЭ) 3-A₁pp (Нм) 1П [(Go₁_gb₁₁/₍__₎ ₍, ₂ 、₎] (13.2) (13.3) (134 )) Заметим, что коэффициент а определяется разностью температур (Т — первая секция нагреваемого участка, коэффициент АА — средняя арифметическая разность температур (т0-Т»), первая и последняя секции, а диакон, коэффициент а] соответствует логарифмической разности температур. * постоянная величина Р, деленная на отношение (9.174).
Коэффициент (7₀__ T;.) a₁p наиболее полезен для фактических расчетов, поскольку он намного слабее к соотношению L / D, чем коэффициенты O]и A₀₀*.Однако этот коэффициент используется не во всех работах. Поэтому при использовании экспериментальных данных по теплопередаче необходимо конкретно указать, как следует рассчитывать коэффициент теплопередачи, если он взят из литературы. Если распределение температуры стенки трубы изначально неизвестно, или физические свойства движущейся среды существенно изменяются по длине трубы, то вычислить коэффициент теплопередачи, определяемый формулой (13.2)-(13.4), очень сложно. в таких случаях принято описывать соотношение (13.1) в дифференциальной форме.
Где величина dQ — интервал длины dz вдоль оси трубы и характеризует количество тепла, отводимого движущейся средой за единицу времени. Оболочка T0-T1 представляет собой локальную разность температур. Аналогично, размер ala представляет собой локальный коэффициент теплопередачи**.Формула(13.5) широко используется в инженерной практике.
В качестве примера течения вблизи поверхности погруженного объекта рассмотрим жидкость или газ, обтекающие сферу с радиусом R, равным Ta, где температура поверхности везде постоянна. Предположим, что температура потока вдали от обтекаемого объекта постоянна во всех точках пространства, равна Yso, Tm + Tn. In в этом случае можно ввести средний коэффициент теплопередачи по всей поверхности сферы. (?= в(4nL2) (G₀-Гос) (13.6) Отметим, что выбор характерной поверхности сферы в данном случае отличается от выбора, сделанного ранее при написании формулы(6.5). Для обтекаемого тела можно также ввести понятие локальной теплопередачи coefficients.
По аналогии с определением(13.5) запишем: (13-7) *Обратите внимание, что для отношения ATjATi = 0.5-2, с максимальной погрешностью 4%, значение DG | P может быть заменено значением DGa, и вместо коэффициента cn, коэффициент aa может быть использован с той же точностью. Такая точность весьма приемлема для большинства практических задач расчета теплопередачи. Иной выбор До тех пор пока форма основной поверхности передачи тепла не будет specified. In по формуле (13.5), площадь элемента dA равна nDdt. Это означает, что коэффициент теплопередачи и температура усредняются по сторонам штрихованного базового цилиндра. 13-1.
- Локальный коэффициент теплопередачи als дает гораздо больше информации о теплопередаче, чем средний коэффициент для теплового потока. Это потому, что он показывает, как тепловые потоки распределяются по всей поверхности тела. Однако в большинстве экспериментальных исследований показан только средний коэффициент теплопередачи, что облегчает его измерение. Следует еще раз подчеркнуть, что удельное значение коэффициента теплопередачи существенно зависит от способа определения значений А и DG.
Кроме того, следует отметить, что коэффициент теплопередачи не является постоянной характеристикой сплошных сред. Напротив, этот коэффициент зависит от ряда переменных: физических характеристик среды (X, q, p, Cp), геометрических параметров системы, скорости течения, характерной разности температур, распределения температур на поверхности теплообмена и др. (что может быть очень трудно).Другой В следующих разделах этой главы описывается, как предсказать зависимость коэффициента а от перечисленных переменных. Для этого обычно составляется корреляция на основе экспериментальных данных и размерного анализа purpose.
Эта теория рассматривает газы, как пространство, заполненное молекулами, которые перемещаются по прямым траекториям, отклоняясь только при столкновении с другими молекулами. Людмила Фирмаль
Во многих простейших случаях(связанных с системами в ламинарной области) коэффициент теплопередачи можно найти непосредственно из дифференциального уравнения конвективного теплообмена transfer. In в случае турбулентного течения разработан достаточно надежный полуэмпирический метод расчета коэффициента а.
Номера этих коэффициентов в наиболее распространенных системах приведены ниже[1]: В разделе 9.6 показано, что при расчете коэффициента теплопередачи между двумя потоками жидкости или газа, разделенными более чем 1 твердым слоем, часто удобно вводить понятие так называемого общего коэффициента теплопередачи K, представляющего собой совокупное влияние сопротивления последовательного соединения теплоты flow.
Кроме того, дается более точное определение величины K, представляющей собой объемную температуру, равную TL и Tc, для описания внутреннего диаметра D«и наружного диаметра D Общий коэффициент теплопередачи K системы определяется с использованием следующего соотношения: Общ = х (13.8) Формула для вычисления K является 1 (1.1 п (Р1/Оо) ■ _ _ _ 1_ \ Dok kdaoao «с2до1» di » I Lok (13.9) Соотношение(13.8)-(13.9) используется при расчете локального коэффициента к. такое определение используется в большинстве случаев Изотермического нагрева Ф = в- Участок некоторых теплообменников / rat (см. Пример 14-2).
Какая передача тепла. Я сделал это. Электрическое сопротивление d1111 tit 11111、 г — (() у одного последователя Т Г » / но. С некоторыми 111, нет. я я н я, ’1,1, ’» с- По формуле(13.8) А U□и(13.9), 1 или Обе стороны теплообмена heat-1_ могут происходить K, параллельный тепловой) 4d ^ c) я Течу по теплу / т ’ по радиации. И затем… / ⁶ Я указал на связь f должно быть соответствующим-Tₜ я 0 z-L» Z-LB Z-Lc круг. Для иллюстрации рис.
Серия экспериментов по определению физического значения коэффициента теплопередачи: коэффициент теплопередачи 1-Длина трубы с нагревательной частью Ла. О, я знаю трубочиста. Lb ’ 3-в одном из И как измерить их при температуре aa°C、 Проанализируйте серию виртуальных экспериментов по межфазной теплопередаче. Пример 13-1.Расчет коэффициента теплоотдачи по экспериментальным данным. На рис. 13-2 показана серия экспериментальных диаграмм, которые нагревают воздух в трубе в состоянии покоя. Первый При внутреннем диаметре трубы 1,27 см сечение z 0, движение происходит в изотермических условиях с температурой th-93,3°C. При z = 0 температура стенки трубы постепенно повышается до T,= 100,3°C.
Эта температура поддерживается на протяжении всего остального участка стенки («>0), ее длина равна Рог равен ба. температура выравнивается с Z=.Подобный O) Lc etc.).Результаты Эксперимент Также koeffi- ich5r (Tig » 1)=? Используйте определение (13.2), чтобы получить: (Ты — гы)= о НДЛ ^ (идти-хз) для Си: Н>вода Гао-гаг-нол ТЗ-го (13.10)) (13.11) (13.12) Аналогично, подставляя соотношения (13.3) и (13.4) в уравнение энергетического баланса (13.10), получаем формулы для коэффициентов aa и ct |ₙ.
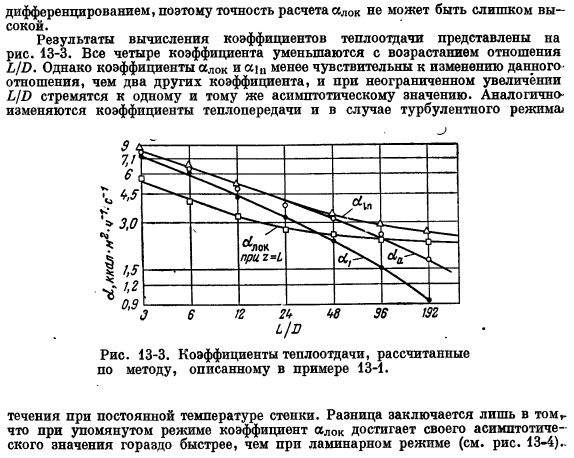
Мы дифференцируем это выражение относительно g и применяем соотношение(13.5). Отсюда И Cₚddib я Лок-НД ДЗ го-га (13.16) (13.17) Если температура Tn не зависит от r, то формула (13.17) принимает вид: ЗАМОК ВКП-Дин (г-га) йа ДЗ (13.18) Производная, содержащаяся в правой части соотношения (13.18), может быть определена из графика зависимости in (G0-Ha) от s. заметим, что нахождение указанной производной связано с графическим Поэтому точность расчета Алок не слишком высока Результаты расчета коэффициента теплопередачи приведены на рисунке. 13-3.
Все 4 коэффициента имеют тенденцию уменьшаться с увеличением отношения, чем другие 2 коэффициента, и то же самое асимптотическое значение с бесконечным увеличением L / D. аналогично, коэффициент теплопередачи изменяется в случае турбулентной области^ 13-3.Коэффициент теплопередачи рассчитывают по методике, описанной в Примере 13-1. Он течет при постоянной температуре стенки. Единственное отличие заключается в том, что в ранее упомянутом режиме коэффициент aLoc достигает асимптотического значения гораздо быстрее, чем в ламинарном режиме (см.
Смотрите также:

