Оглавление:





Полуэмпирические выражения для турбулентного потока энергии
- В предыдущем разделе мы показали, что новый член отображается в результате усреднения уравнения накопления энергии во времени. Это можно интерпретировать как часть концепции турбулентного потока энергии g *ⁿ. Решив усредненное уравнение сохранения энергии и получив усредненный температурный профиль, необходимо принять соотношение между значениями d ’ 11 и T. Ниже приведены некоторые из наиболее часто встречающихся соотношений в литературе. Вихревая тепловая. По аналогии с законом теплопроводности Фурье можно принять следующую формулу: (12.9). Значение L. является частью этого отношения, называемого турбулентной теплопроводностью или вихревой теплопроводностью conductivity.
Следует отметить, что величина » 1 ″ не является мерой физических свойств конкретной жидкости, а зависит от пространственных координат, направления и характера турбулентного движения. Вихревая вязкость v, ⁿ= p. * ’/ P и вихревая теплопроводность a ’ * ’ =A. н,/рР выражаются в тех же единицах. Нам удалось оценить турбулентный перенос импульса и отношение vcfⁱ / e».В общем случае это отношение оказалось порядка 1.In в литературе по турбулентности приведены различные численные значения этого соотношения.
Однако при малых абсолютных давлениях газ частично теряет характерные свойства непрерывности и появляются являения, которые могут быть объяснены, только если принимаются во внимание представления о молекулярном строении газа. Людмила Фирмаль
Расход воздуха в аэродинамической трубе[3] отношение v, v4aa>изменяется от 0,7 до 0,9 и, подобно струе[4], то есть в состоянии»свободной турбулентности», приближается к 0,5. Формула смешанного паса Прандтля и Тейлора. Согласно теории Прандтля, механизмы турбулентного переноса импульса и энергии являются same. So, по аналогии с формулой(5.15), можно записать следующую формулу: (12.10) Значение I называется путем смешанного Прандтля. Заметим, что соотношение (12.10) подтверждает выполнение условия v,, l / a = 1.Вихревая теория переноса напряжения Тейлора[5], m’ и g, для первой теории должны быть разными. На практике это будет= 0.5 от теории Тейлора. Именно так.
По этой причине общепринято, что эта теория в первую очередь эффективна в отношении потока грузовиков и струй, но область применения теории Прандтля ограничена потоком газов и жидкостей в трубах. [4]в этом случае прандр рекомендует следующую формулу для прохождения смешивания: Z = xii/, где y-расстояние от стенки. Представление, основанное на гипотезе портрета кармана. Присвоение формулы кармана смешанного пути отношению (12.10) приводит к зависимости. 7.- * NPC ( Х / г|,») » | Где ha-та же константа, что и выражение (5.16).Выражение (12.11) и выражение (12.10) справедливы в предположении, что выполняется условие v ⁽, /eⁱⁿ= 1. Эмпирическая формула десслера для течения теменной кости region.
- Чтобы иметь возможность объяснить процесс теплопередачи в области течения, непосредственно прилегающей к твердой поверхности. Известно, что Формулы Прандтля и кармана несправедливы, Дейслер предложил следующую эмпирическую формулу: (12.11 9 с’) = — ПФУ₽НСИ> Дж. р {л-ехр(-н ^ / х)} ^- (12.12) Эмпирическая константа n, показанная здесь, имеет то же значение, что и аналогичное выражение для потока импульса(5.17).Формула (12.12) описывается в предположении, что механизм передачи импульса и энергии один и тот же, то есть v» ’/ a’» = 1.В Примере 12-1 используется приведенная выше мпирическая зависимость. Где A-константа.
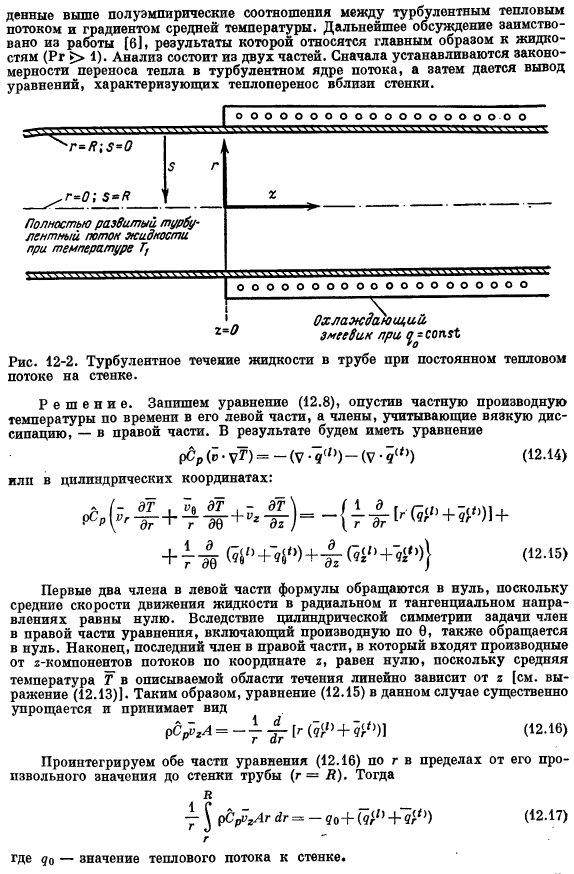
Обратите внимание, что анализ проводился по проблеме температуры, рассмотренной в разделе 9.8. (12.13) Первые 2 члена слева от выражения исчезают, потому что значение равно нулю. Из-за цилиндрической симметрии задачи правый член уравнения, содержащий производную от 0, также будет маркирован. Наконец, последний член справа, включая производные Итак, формула (12.15) в данном случае значительно упрощается, принимая следующий вид: ПК ^ га = -м ^ г [г(г, г’,+?г»)] (12.16) В диапазоне от его абсолютного значения до стенки трубы (r =Я) он интегрирует обе стороны уравнения (12.16) относительно r. а затем… -J (£^>rArdr = — р₀++’?»») (12.17) Где dc-это значение Тепловой поток _regions т р р р б Y.
Поток и явления переноса тепла при таких условиях непрерывности среды могут быть адекватно выражены через критерии Рейнольдса, Маха, Нуссельта и Прандтля. Людмила Фирмаль
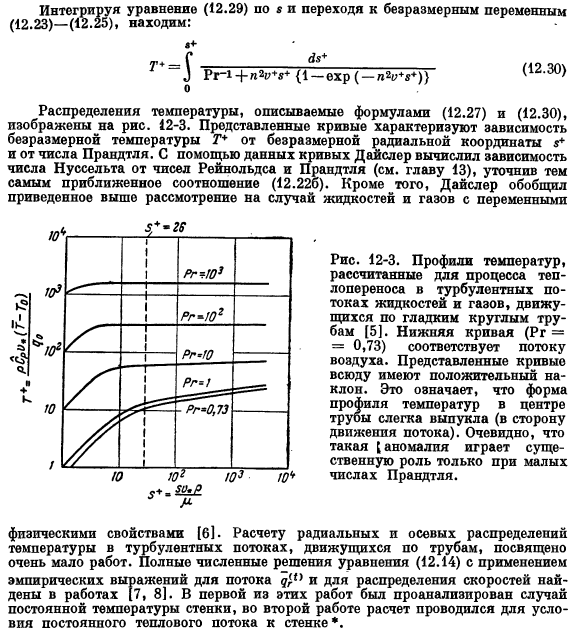
Кроме того, фактические члены. Из центра потока, если вы игнорируете левую сторону отношения (12.17), область является ignored. In турбулентное ядро, вы получаете Паз (12.21) Получение путем замены строгих рейвов Вызывается отношением(5.21).Получаем уравнение(12.20), далее. В некоторой степени Для всех R, принятых Прандтлем e, не является полностью оправданным предположение mu о том, что градиент температуры не играет роль центра трубы. Смешайте длину пути Закрепите формулу (12.21) в диапазоне от постоянной опорной плоскости i = s до любой поверхности i. (12.22) (12.226) Экспериментальные результаты для Pr = 1 хорошо объяснены.
Самым простым уравнением, соответствующим экспериментальным данным и выраженным в аналогичной форме соотношению (12.226), является уравнение Чилтона-Колборна(13.36). Dysler [61]выбирает в качестве эталона сторону, разделяющую буферную зону и турбулентное ядро surface. In в этом случае соотношение (12.22) должно означать, что профили скорости и температуры в турбулентном ядре подобны друг другу.
Смотрите также:

