Оглавление:





Сопротивления по длине. Гидравлический коэффициент трения.
Сопротивления по длине. Гидравлический коэффициент трения. Рассмотрим сопротивление цилиндрической трубы В устойчивой части потока (см. рис. 6.6). в этом случае 5K = 0 и 5b = 5c представляют собой цилиндрические грани всех точек, где cos (n, x) равен 0.In кроме того, все точки на поверхности 5b имеют равные условия (поток стабилизируется), поэтому m = m0 = const.!, То есть мы также учитываем, что Cy = const1, cos (m, x)= −1 5r = 5a = 50, то есть 5X = 1, перепишем формулу (6.17) в следующем виде: Совместно Su5s / 50. Он показывает периметр раздела 50 с x и вводит количество= 50 / x. It называется гидравлическим радиусом.
Где выражение (6.18) принимает вид: Для круглой трубы P = 02/4, где d-диаметр трубы. Если мы введем обозначение K = 4C /, то получим зависимость в этом случае (6.23) Определяют потери давления по длине круглой трубы и называют Вайсбах-д’Арси официальным. Из Формулы (6.21) вы получите еще 1 важное соотношение. Учитывая значение коэффициентов E0 и Cy, умножим обе стороны уравнения (6.21) на pn | / 2. (6.24) Последняя формула является основой для равномерного движения жидкости и связывает силовую характеристику потока M0 с энергией LD. In в будущем он будет использоваться для получения других важных зависимостей. 147. Рассмотрим более подробно сущность суммы х формулы(6.23).
Коэффициент трения отличается только постоянным коэффициентом, который называется коэффициентом гидравлического трения. Людмила Фирмаль
- Очевидно, что это зависит от тех же параметров, что и C/. Параметр а определяется профилем скорости вблизи стенки и одинаков в кинематически сходных течениях, где безразмерные диаграммы скоростей одинаковы. Однако, как видно из нижеследующего, сходство скоростных диаграмм круглых труб строго обосновано и подтверждается только опытом ламинарного течения. Геометрическое сходство всегда имеет место, так как параметр A не зависит от Pe и одинаков для всех круглых труб с гладкой поверхностью. walls. As опыт показывает (см. ниже), что малая шероховатость стенки не влияет на X, и, несмотря на то, что строго говоря геометрическое подобие нарушается, закономерность (6.25) остается в силе. Но если стены достаточно шероховатые, то величина X должна зависеть от формы и расположения неровностей. По результатам эксперимента, если измерить среднюю скорость V и перепад давления Np, то коэффициент X можно определить по формуле (6.23).
- Раздел 6.4 содержит руководство по разумным, теоретически обоснованным способам обработки таких экспериментальных данных. Согласно формуле (6.25), необходимо найти эмпирическую зависимость X от численного Ke и безразмерных параметров, определяющих геометрическое подобие течения. Для гладких круглых труб Этот параметр не требуется. Все круглые трубы геометрически подобны, так как экспериментальная точка X = X (Ke) на графике образует единую кривую. Однако требования к геометрическому подобию распространяются не только на форму поперечного сечения, но и на форму выступов неровностей стенок, так что грубые трубы геометрически не похожи.
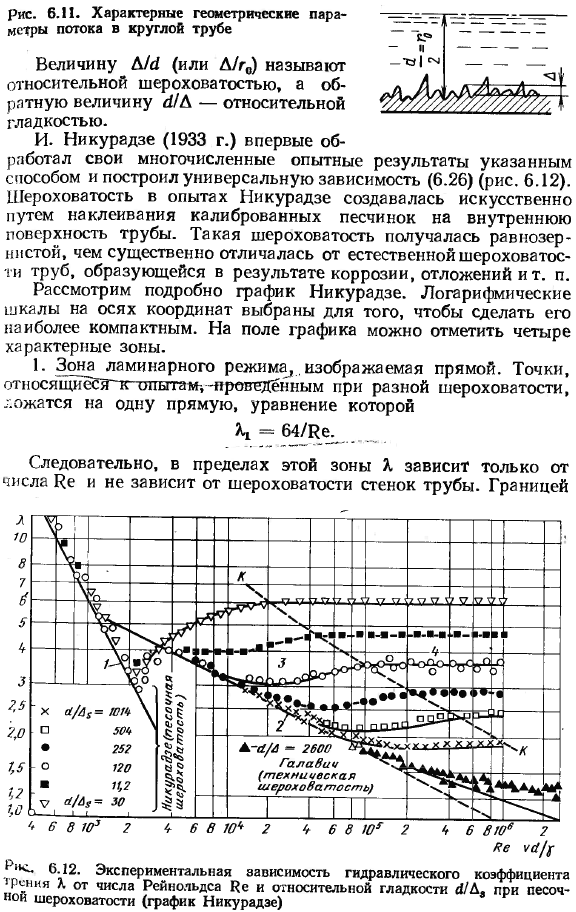
Но тогда, при строгом подходе, практически невозможно найти 2 геометрически похожих трубы с естественным roughness. So, как приближенное предположение, радиус средней высоты шероховатости A r0 или диаметр c! Предполагается, что отношение по отношению к грубой трубе является геометрическим similar. It будет то же самое(рис.6.11). Затем необходимо обработать экспериментальные данные в виде кривой Значение Uy (или AUr0) называется относительной шероховатостью, а u! Обратная величина D называется относительной гладкостью. И. Никурадзе (1933) впервые таким образом рассмотрел свои многочисленные экспериментальные результаты, построив универсальную зависимость (6.26) (рис.6.12).
Шероховатость в экспериментах Никурадзе создавалась искусственно путем приклеивания отрегулированных песчинок к внутренней поверхности трубы. Людмила Фирмаль
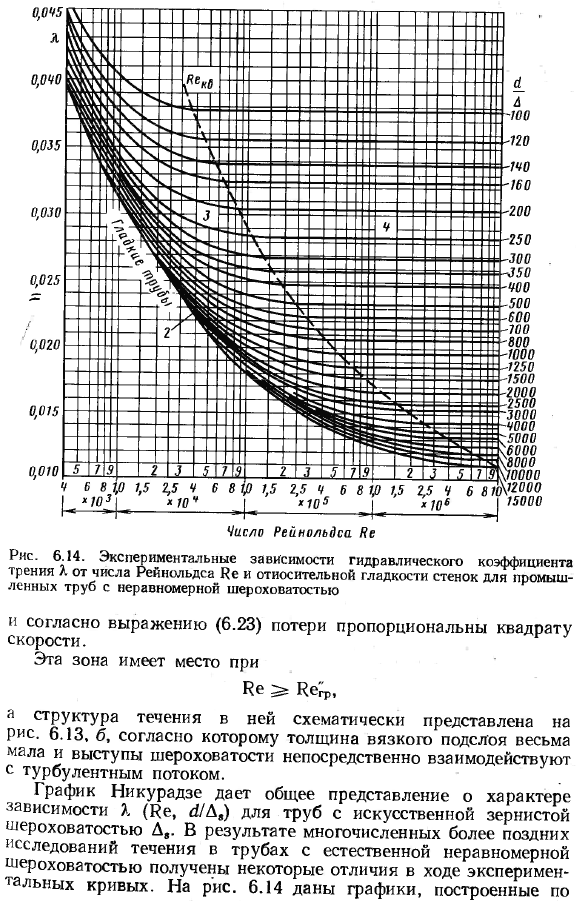
- Такая шероховатость получилась равномерной и значительно отличалась от естественной шероховатости трубы вследствие коррозии, отложений и т. д. Рассмотрим подробно график работы Nikuradze. To чтобы сделать его максимально компактным, выбирается логарифмический масштаб осей. В поле графика отображаются 4 характерные зоны. 1.Зона ламинарного течения, проведенная по прямой линии. Точки, связанные с экспериментами, выполненными с различными шероховатостями, находятся на 1 Прямой линии, и их уравнения являются Так, в этой зоне к зависит только от количества Пэ и не зависит от шероховатости стенок трубы.
Граница Подслой Зона-это координата абсциссы ’1§ 2300 =1§Kekr. So, эта закономерность возникает в»он» Кекр, то есть в ламинарной области в pipe. In кроме того, согласно формуле (6.23), потери линейно зависят от скорости. Переход от ламинарного течения к турбулентному происходит в диапазоне He = 2300-4000.В потоке наблюдается неустойчивость, обусловленная периодическим возникновением очага турбулентности и его исчезновением. 2.Зона гладкого пристенного течения образована экспериментальными точками, расположенными вдоль другой прямой. Где X также не зависит от шероховатости.
Смотрите также:
Возможно эти страницы вам будут полезны:

