Оглавление:












Использование уравнений сохранения для решения задач о теплообмене
- Глава 3 показала, что гидродинамическую задачу гораздо легче и надежнее сформулировать на основе общей системы уравнений непрерывности и движения, чем составить дифференциальный баланс массы и импульса для каждого частного случая. Аналогично, как видно из приведенного ниже, наиболее рациональным способом постановки задачи теплопередачи является использование системы уравнений непрерывности, движения и энергии. В отдельных случаях эта система может быть упрощена путем игнорирования некоторых effects.
To проиллюстрируем возможные способы упрощения, учитывающие специфические условия теплообмена в различных системах, рассмотрим следующие примеры: большая часть из них связана с использованием обыкновенных дифференциальных уравнений. Более сложные системы, которые представляют интерес с точки зрения инженерной практики и могут быть объяснены только с точки зрения систем уравнений в частных производных, описаны в Главе 11. Прежде чем перейти к анализу этих примеров, мы покажем, как дифференциальное уравнение (9.152), описывающее теплообмен при ламинарной вынужденной конвекции в длинной круглой трубе, выводится из уравнения сохранения.
Этот процесс, однако, связан с обменом тепла и работой между различными слоями газа, даже в том случае, когда твердая поверхность не обменивается теплом с омывающим газом. Людмила Фирмаль
При этих условиях и= » е=9е=0. Если предположить, что все физические свойства среды постоянны и отсутствует диссипация вязкой энергии, то уравнение сохранения, описанное в цилиндрической системе координат, выглядит следующим образом: Непрерывные уравнения (10.30) Уравнение движения (10.31) Уравнение энергосбережения (10.32) Имея в виду уравнение непрерывности, вы можете сделать левую часть уравнения движения равной нулю и опустить последний член в правой части. Тогда уравнение движения легко интегрируется. В результате получается параболическая скорость profile. It уже выведено и объяснено в разделе 2.3.Подставляя этот профиль в уравнение (10.32), последнее принимает вид (9.152).
Таким же образом мы сделали соответствующее упрощение в уравнении сохранения, поэтому мы можем сформулировать другие задачи, представленные в главе 9. Заменить распределение (10.33) Выполните уравнение(10.34) и то, которое дает следующее уравнение Id / dT и я делаю?* ⁴ *gg dr v dr U ’ 1 ’(1-X*) » H (10.35 утра)) Последние следуют за B Полезно перед (10.38) (10.39) Джи, ты знаешь? Яростный Зависимости Температурный профиль выглядит следующим образом: E =(L +1-SJ-2)-(AG + 1-LOG «) |, Находим: (10.40 утра)) Кг1-г.)(1-Х2) » Последний тост.
Вы можете рассчитать его из отношение к уравнению. Интерфейс фильма, вы можете легко получить про (10.46) и распределение по температурам Г-н гр х Tₜ-Т (10.47) По распределению (10.47) Фильм x-координата. Из-за этого, согласно теории Айлинга、 Значение вязкости, отношение И затем (10.48 в) Где B-конкретная константа опыта[опорное выражение (1.43)].Сочетание Сжигание равенства очень жесткое-Tₜ.Здесь при применении соотношения: p [S (T₀—Tₜ) IT, tₜ) формула (10.486) содержится в следующей формуле распределения (10.48 б) _ _(Pgcosp \Г6-12Г1+(х/ЦIn(р,/щ)) 1 + в(И₈/цо) 1 ’\РО) L1P(НС / м) в J [(у / РО)*’) (Ра / Ро) Дж (10.49) Формула (10.53) может быть интегрирована 2 раза.
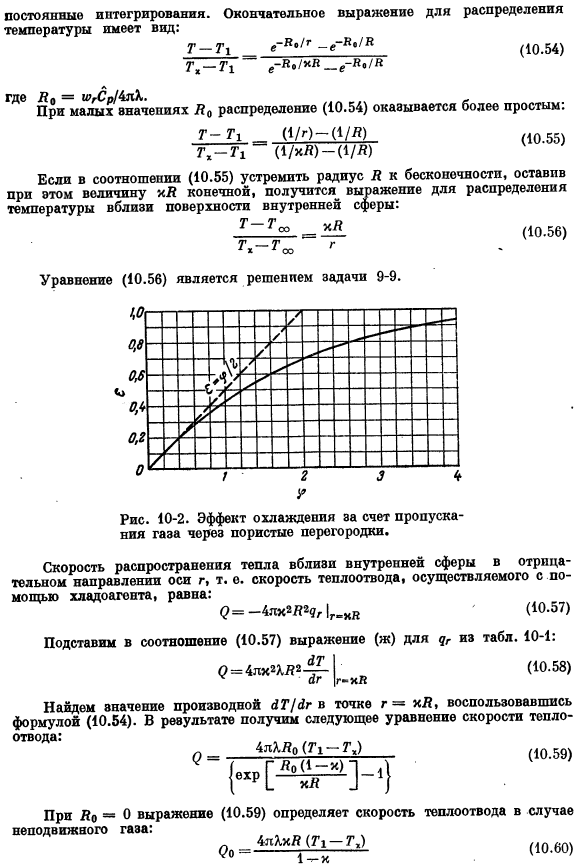
- Заданную температуру на стенке наружной и внутренней оболочки можно найти Непрерывная интеграция. Окончательное выражение распределения Температура biГ, Г1е-Я я./r_e-р./ Б 00.54) Т — — — е-ти-я./ Xv_e-я./ » Где B0 = ВПИК / инструмент. Если значение Bo невелико, то мы можем видеть, что распределение (10.54) проще. (10.55 утра) Рис. 10-2.Эффект охлаждения при пропуске Газ проходит через пористую перегородку. (10.57)) (10.58) Используя формулу (10.54), найти слияние дифференциала dT / dr в точке r = xB. В результате получается следующее уравнение теплопроводности: 4яШо(Г1-Г) (10.59) (10.59) для определения коэффициента теплоотвода корпуса _4lxxb (Г1-г.
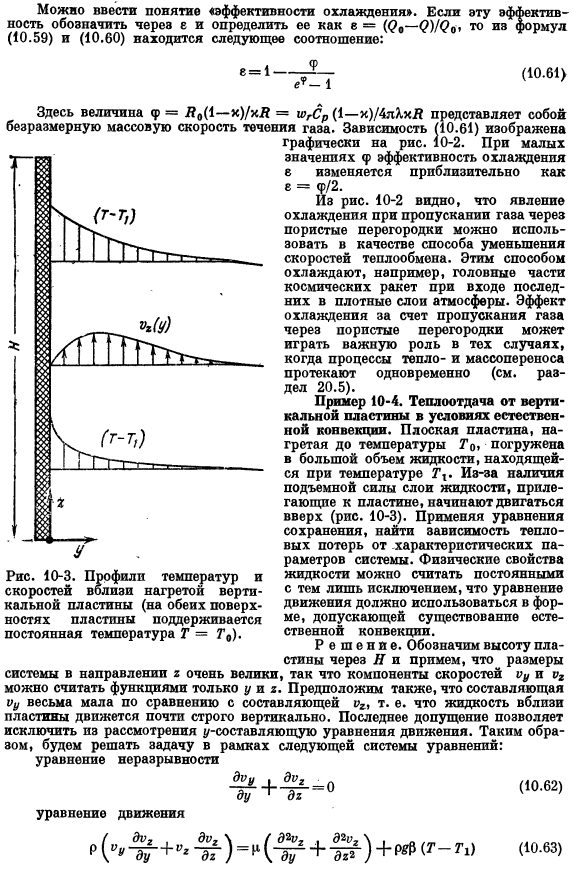
Можно ввести понятие эффективность охлаждения. Обозначим эту эффективность через e и определим ее как e =(Q, — Q) / Qₒ (10.59) и (10.60) нашли следующую связь. Е = 1 — (10.61). Безразмерный ( Встречайте решение этой системы、 Безразмерная скорость Уравнение сохранения Граничное условие (10.75) Безразмерное расстояние (10.64) Часть уравнения (10.74) окружность выглядит так: 1ДЖ = ОО £ = — ОО Ф «= ФЗ = 0 0 = 1 Фр = ФГ = 0 0 = 0 фр = ф» = 0 0 = 0 (10.76) (10.77)) (10.78) ДЗ Залить по безразмерным параметрам.
Так как уравнение (10-10) выведено на основании первого закона термодинамики, то оно справедливо не только для случая изоэнтропического изменения скорости, но и для тех случаев, когда скорость падает до нуля без притока или оттока тепла и без приложения внешней работы. Людмила Фирмаль
Средний тепловой поток от поверхности пластины, такой как: 9 тонн = А(Гв-Г、) (10.80)) Безразмерная температура, а следовательно, и дифференциал dv / dm\, зависит от μ, t и Pr. Поэтому значение производной при q = 0 должно определяться только по T и Pr. Следовательно, определенный интеграл? Это должна быть безразмерная функция числа Прандтля. Основываясь на предыдущем выводе, эта функция (обозначенная C в Формуле (10.80)) является очень слабой, приблизительно Лось-0,548.После этого была проведена более жесткая процедура, позволившая установить очередную зависимость C Pr… С…………. 0.612、 А (р» х)= о (10.81) Последнее уравнение-это уравнение (k) в таблице.
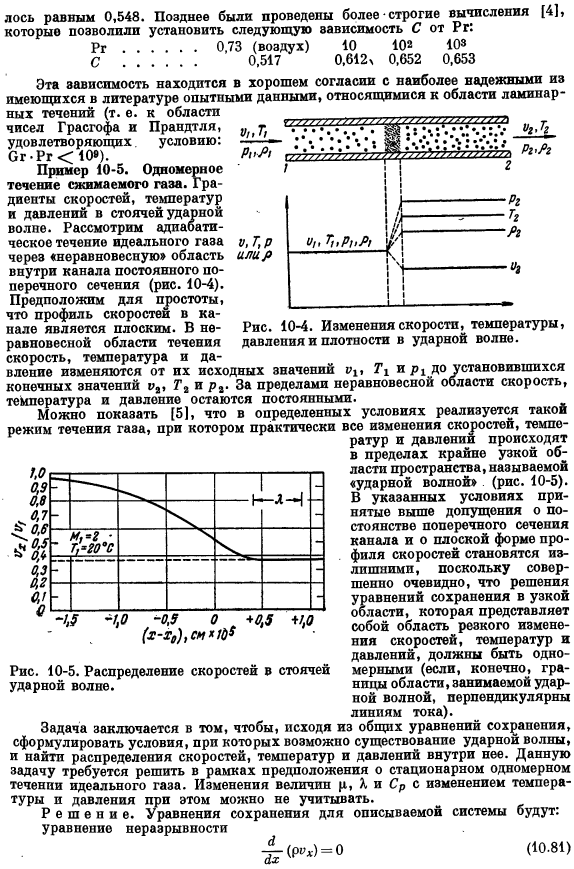
Условия (1nJ / dr) описаны в случае стационарной области теплопередачи с использованием Р = 1, что является эффективным для идеального газа. Уравнение неразрывности может быть легко интегрировано. Если значения плотности и скорости невозмущенной области течения на левой стороне ударной волны представлены p и t>] (см. рис. 10-4), то уравнение (10.81) выглядит следующим образом: Используйте уравнение перемещения yuotn для исключения из уравнения сохранения энергии. В результате, вы можете увидеть следующее: dvₓ, 4 м д 3 «П»!»ля» (10.84) dt С » — ДТ- Это уравнение может быть выполнено 1 раз. Получается следующее выражение: Th.
После простого преобразования. Еще лоб (10-88) (10.87) (10.89)) Непрерывная интеграция Не эмульгированных поток, номера ДВ / ДХ =0.Соотношение полов (10.89) значение vₓГ1, найти: CW = + p, i>? = = Пи(Б?+ ЯТ,/ М). Используя равенство! Форма Ульв Выражение (10.90) может быть представлено в следующей безразмерной форме: H> = ₽Ma Mai(Ф-1) (Ф—а) Безразмерные переменные, содержащиеся здесь, определяют безразмерную скорость (10.91) Безразмерное расстояние (10.94) (10.95) (10.96)) Характерная длина X-это средняя длина свободного пробега молекулы газа. Используя формулу (1.19), мы можем исключить значение P из уравнения X, заданного кинетической теорией gases.
В результате для X получим следующую формулу: (10.97. Если при интегрировании уравнения (10.91) получаются следующие результаты: (10.98) * Число Маха my представляет собой скорость k. скорость звука при температуре Проверьте показатели успеха 10-10 и 10-15). Формула (10.98)) Используйте идеальное уравнение состояния Подарок.
Смотрите также:

