Оглавление:






Вынужденная конвекция
- Основное внимание в предыдущем разделе было уделено теплопроводности твердых тел. В этом и следующем разделах описаны 2 предельных случая теплообмена жидкостей и газов, вынужденная и естественная конвекция (или естественная конвекция). Наиболее характерные черты этих ограниченных случаев перечислены и показаны в таблице. 9-2. Временно самая практически важная проблема теплопередачи была произвольно отнесена к 1 из этих ограничительных случаев. Однако для некоторых задач оба типа конвекции необходимы одновременно. В данном разделе анализируется проблема стационарного форсированного convection.
В некоторых ограниченных случаях эта задача оказывается очень простой и может быть решена аналитически[4, 5].Поэтому рассматривается задача конвективного теплообмена в ламинарном потоке вязкой жидкости, движущейся по кольцевой трубе. Предположим, что физические свойства жидкости (p, q, X и Cp) постоянны. Радиус трубы обозначается через R, предполагая, что область z 0 имеет постоянную температуру жидкости, равную to>, в то время как область z> 0 внутренней стенки трубы поддерживает постоянный тепловой поток, равный dg. Эти условия Например, это реализуется, когда трубы равномерно обернуты в электрическую нагревательную катушку. Как показано в таблице.
При высоких сверхзвуковых скоростях выделение тепла в пограничных слоях, которые окружают поверхность движущегося тела, создает чрезвычайно высокие температуры. Людмила Фирмаль
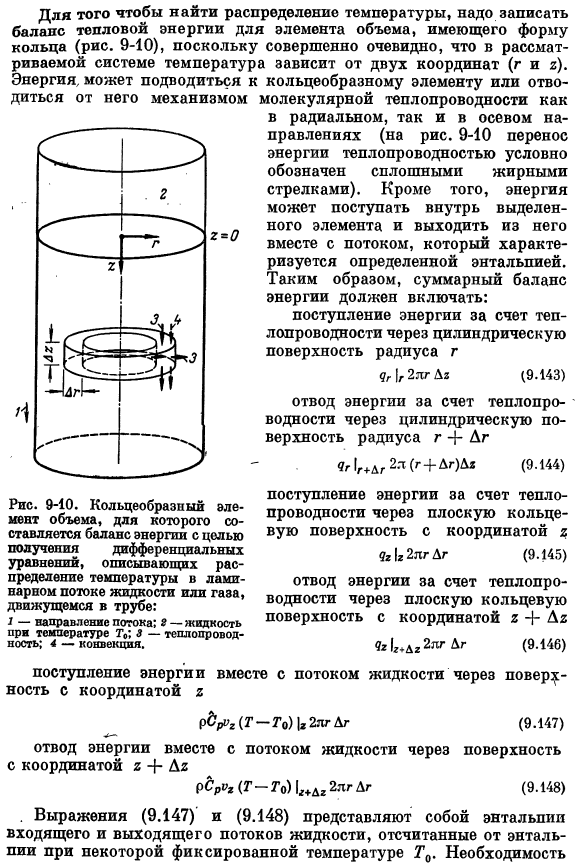
Первым шагом в решении задачи теплопередачи при вынужденной конвекции является нахождение скорости profile. In в разделе 2.3 на основе метода баланса импульса в тонком слое получена формула распределения скоростей в ламинарном потоке. Здесь величина гтахтах связана с перепадом давления по длине трубы отношением t > ᵢₘₐₓ = (po — PB) R2/ 4PL. Для нахождения распределения температуры необходимо описать тепловой энергетический баланс объемного элемента в виде кольца (рис.
Очевидно, что в рассматриваемой системе температура зависит от 2 координат (g и g). Энергия может подаваться на циклические элементы или молекулярную молекулярную проводимость, как радиальную, так и осевую (на рис. 9-10 перенос энергии за счет теплопроводности условно обозначен толстой сплошной стрелкой). flow. It характеризуется определенной энтальпией. Таким образом, общий энергетический баланс включает в себя затраты энергии за счет теплопроводности через цилиндрическую поверхность радиуса.
- Отвод энергии теплопроводностью через цилиндрическую поверхность радиуса r + Dg qᵣ|ᵣₜ₄ᵣ2n (G + DG) D » (9.144). Ввод энергии теплопроводностью через плоскую кольцевую поверхность в координатах z?₁ / ₁2lgDg(9.145) Отвод энергии теплопроводностью через плоскую кольцевую поверхность координаты z + Yes DGGS, Lg2lgyyg(9.146) Поток жидкости (9.147) Ввод энергии по координатам РДР!> Р (Т — гв)|, 2lrDr Поток жидкости через поверхность с координатой z и отводом энергии+да rSdMG-T₀)| » D₁2yagDg(9.148) 。Уравнения (9.147) и(9.148) представляют собой энтальпии входящих и исходящих потоков жидкости, которые отсчитываются от энтальпий при определенной фиксированной температуре до.
Необходимость Выбор точки отсчета температуры объясняется тем, что только относительная величина, а не абсолютная, обусловлена потоком энергии. плоскость, соответствующая началу координат z, может быть выбрана совершенно произвольно. Его расположение, как видно ниже, не фигурирует в дифференциальном уравнении переноса. Если приравнять поток энергии, направленный внутрь к отдельным кольцевым элементам объема, к потоку энергии, направленному наружу, то получится формула энергетического баланса. Уравнение Rae для 2ndrdg имеет вид: (9.149) Затем мы принимаем значение Δr к нулю и получаем дифференциальное уравнение теплопередачи.
Внутренняя энергия может быть записана как произведение теплоемкости на температуру, и поэтому температура будет возрастать в таком потоке по его направлению, указывая на тот факт, что внутренним трением энергия давления была превращена во внутреннюю энергию. Людмила Фирмаль
Подставляет распределение скоростей этой формулы, которое характеризуется формулой (9.142), и использует закон Фурье теплопроводности для представления теплового потока qᵣ и qz в радиальном и осевом градиентах температуры. (9.150) (9.151) В результате получается следующее уравнение в частных производных: — (Т В (9.152) Обычно вклад теплопроводности в z-направлении, описываемый термином dTT1dg, r, в правой части уравнения (9.152) мал по сравнению с вкладом конвективного переноса пропорционально dT / dz. Поэтому член d2tldz2 вообще не рассматривается. Но есть системы, где недопустимо пренебрегать продольной теплопроводностью.
Если уравнение (9.152) опускает член, соответствующий теплопроводности в направлении z, то оно принимает вид: Решение этого уравнения, определяющего температуру в трубе как функцию координат направляющей, должно удовлетворять следующим граничным условиям: (9.154) (9.155) (9.156) Для удобства дальнейших расчетов введем безразмерные Переменная: (9.157) (9.158) (9.159) В новой переменной уравнение распределения температуры выглядит следующим образом: Граничные условия переписываются следующим образом: 0 для 5 = 0 £= 0 в 0-0 (9.161) (9.162) (9.163) Точное решение уравнения граничного условия (9.161)-(9.163) (9.160) была получена в[6]. не стоит приводить ее сюда полностью.
Однако интересно проанализировать асимптотическое поведение температурного профиля с большой безразмерной вертикальной координатой value. In таким образом, на значительном расстоянии (вниз по течению) от начальной точки нагреваемой части трубы наличие постоянного теплового потока на стенке должно увеличивать температуру и быть прямо пропорционально координате£.кроме того, если величина J велика, то предполагается, что форма радиального температурного профиля не зависит от величины.
Представляется целесообразным поиск асимптотического решения уравнения (9.160), соответствующего большому значению координаты£в виде: c = c’OC — + ChG(6> (9.164) Где Co-константа, необходимая для расчета Решение Задача. Очевидно, что функция, определенная в выражении 0, равна 0(E,£) (9.164) не является точным решением проблемы. Эта функция может одновременно удовлетворять выражению (9.160) и граничным условиям (9.154) и (9.155), но она не может быть использована для надежного удовлетворения граничных условий (9.156)… Вместо условия(9.156), другое граничное условие, то есть: — 2nflzgi = J с J с£п (т —T₉) в? риф ок.
Это последнее условие означает, что количество тепла, поступающего в трубу через стенку, равно je между количеством тепла, проходящего через поперечное сечение трубы£=£ £ и£ = £ = 0. Подставляя выражение (9.164) в выражение (9.160), получаем следующее обыкновенное дифференциальное уравнение для функции Y: ТТ(Е5) Мы интегрируем это уравнение с ξ 2 раза, подставляя результаты интеграла в Формулу (9.164). (9.167) с = С * £ + С «— ’ Гб ’)+ C1lⁿ£+(-> Здесь Cx и Cr являются произвольными константами и, как и константа Co, могут быть найдены из граничных условий, сформулированных выше.
Константы Co, Ci и C₂ равны следующим значениям: Если присвоить эти значения справа от выражения(9.168): * + ‘ + ^- Уравнение(9.172) определяет температуру как функцию безразмерной радиусной координаты£и безразмерной ординаты£.является ли эта формула точной в крайних случаях?. Однако даже при£ 0,1 локальная температура, предсказанная в уравнении(9.172), отличается от точного значения лишь на 2%. Если вы знаете распределение температуры, вы можете рассчитать средние характеристики температуры field. In исследование конвективного теплообмена в практически постоянной жидкости (9.172) значения p и C обычно работают при средней температуре 2-х типов.
Джей Джей (9.173). Средняя температура обоих является функцией z-координат. Значение представляет собой среднее арифметическое локальной температуры на любом поперечном сечении потока. «Объемную» температуру Th, как правило, можно измерить, разрезав трубу, по которой течет теплоноситель в сечении z, собрав вытекающую из трубы жидкость в емкость и тщательно перемешав ее. По этой причине среднюю температуру Th иногда называют «температурой полного перемешивания «или»средней температурой всего потока».
В заключение, введенная выше безразмерная геодезическая ξ может быть переписана следующим образом: Что (о п) (mµe П) (Л) ((Л) Л)) (9.175) Где d-диаметр трубы. Re — это число Рейнольдса, определение которого было дано ранее. Pr =Cₚp / A-это число Прандтля. Глава 10 показывает, что числа Рейнольдса и Прандтля появляются во всех задачах конвективного переноса.
Смотрите также:

