Оглавление:



Теплоперенос внутри ребристой поверхности нагрева
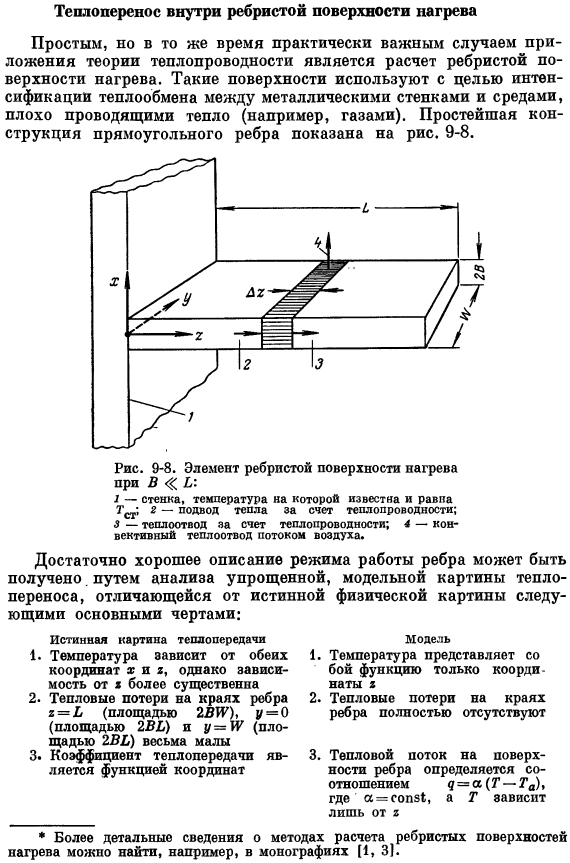
- Применение теории теплопроводности является простым и в то же время практически важным случаем расчета оребренной поверхности нагрева. Такие поверхности используются для усиления теплообмена между металлическими стенками и плохо проводимыми теплоносителями (газом и др). Простейшая структура прямоугольных ребер показана на рисунке. 9-8. Достаточно хорошее описание режима работы ребер может быть получено путем анализа упрощенного модельного изображения теплопередачи.
Температура зависит как от координат x, так и от r, но зависимость от 1 более важна 2.Теплопотери на концах ребер t = L (площадь 2BW), p = 0 (площадь 2M) и y = и (площадь 2BL) очень малы 3.Коэффициент теплопередачи является координатной функцией 1.Температура-это просто функция 2.В конце ребра нет абсолютно никакой потери тепла Тепловой поток на поверхности ребер определяется соотношением* Поверхность * Более подробную информацию о способах расчета оребренного нагрева, например, можно найти в монографиях (1, 3). Напишите уравнение для теплового энергетического баланса в разрезе ребра длины Az (см. рис. 9-8).
Единственно, что требуется дополнительно, — это знание коэффициента восстановления для частного слоя, откуда можно определить температуру восстановления. Людмила Фирмаль
Разделите это уравнение КЗ \ I2BW — Q, а\ з z2BW-а ^ (2Wtii) (г-га)= 0 (9.125) на 2BWru и передайте его пределу как AZ — ►0.В результате получается дифференциальное уравнение. 22⁶ В этой формуле подставим закон Фурье теплопроводности= — KdTIdz, rjifi X-теплопроводность металла conductivity.
В случае постоянной теплопроводности можно увидеть следующее: * ^- =- ^- ⁽⁽⁽(9-127) Это уравнение должно быть решено при граничных условиях Т = Т » У » = 0(9.128) (9.129) Для удобства введем безразмерные переменные, определяемые следующим образом: Безразмерная температура 6 = Gst-g’a ⁹13⁰⁾ Безразмерное расстояние С = — £9.131) Безразмерный коэффициент теплопередачи (9.132) В новой переменной задача о граничном значении, сформулированная выше, будет иметь вид: (9.133) (9.134) (9.135) Общее решение уравнения (9.133) представляет собой линейную комбинацию гиперболического синуса и гиперболического Косинуса.
- Любые константы, содержащиеся в этом решении, можно найти из граничных условий(9.134) и (9.135). После простого расчета, это выглядит так: 0 = ч(нет) — е н ш(с?) Выражение (9.136) может быть преобразовано в форму Охпвд-Д) ⁰ — (9.136) (9.137) Следует подчеркнуть, что эта формула эффективна только в том случае, если теплопотери по краям ребер незначительны «Эффективность ребра» d) определяется как: Heatg тепло фактически рассеивается поверхностью ребра.
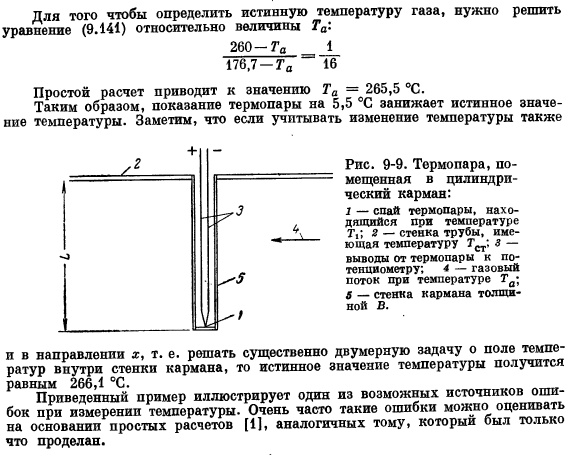
Потери тепла при температуре ТСТ поддерживается(в постоянных) Для задач, которые мы рассмотрим в этом разделе, теоретическое значение q равно: Джей Джей а (Т —Tₐ) dzdy ы|_?ГТ ————— Джей Джей а (Tₐ-Tₐ) dzdy Если вы подставите здесь выражение (9.137), то увидите следующее: (9.139) Где N-безразмерная величина, определяемая соотношением (9.132) Пример 9-3.Погрешности, возникающие при измерении температуры с помощью термопары. На рис. 9-9 показана термопара, вставленная в цилиндрический карман, окруженный потоком газа.
Чтобы сделать этот вывод, необходимо принять во внимание тот факт, что уравнение энергии для пограничного слоя является линейным относительно температуры. Людмила Фирмаль
Если температура G, указанная термопарой, равна 260°C, найдите ее истинную температуру. Температура карманной подставки Т «= 176,7°C; a = 153,7 ккал-м — ’-i-i. * 0-1; K = 27,56 ккал — м ^ — h «1-C» 1; толщина стенки кармана B = 2 мм; длина кармана L = 6,1 см. Решение. Карман с термопарой внутри будет контактировать только с потоком газа снаружи. Толщина стенки кармана меньше по сравнению с его диаметром. Поэтому распределение температуры по длине стенки должно быть примерно таким же, как распределение температуры по длине Толстого ребра 2B, контактирующего с потоком газа с обеих сторон.
Согласно формуле (9.137), безразмерная температура на дне кармана (измеренная с помощью термопары) равна: истинное значение температуры оказывается решением X-направления n, то есть по существу 2-мерной задачи о температурном поле внутри стенки кармана Приведенный пример показывает 1 из возможных причин ошибки, основанной на простом расчете[1]. Для простого расчета это будет значение Ta = 265,5°C. Поэтому, чтение термопары 5.5°C рисует вне истинную температуру value.
Смотрите также:
| Теплообмен при наличии химического источника тепла | Вынужденная конвекция |
| Теплоперенос через многослойные стенки. Аддитивность тепловых сопротивлений | Естественная конвекция |

