Оглавление:







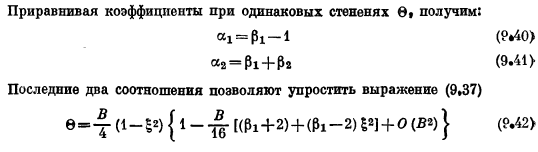

Теплообмен при наличии электрического источника тепла
- В качестве первого примера рассмотрим процесс распространения тепла в проволоке круглого сечения. Радиус провода через K и его проводимость, выраженная в 0m «1-cm» 1, обозначаются через-L. E. пропускают ток плотности / a-cm-2 к проводу. Прохождение электрического тока зависит от того, какая часть электрической энергии преобразуется (в тепловую энергию) в тепло. Тепловыделение на единицу объема проволоки характеризуется следующей формулой: волна | g означает, что количество вещества берется на поверхности радиуса R. Движение энергии происходит в положительном направлении оси Z. Используйте выражение (9.4)-(9.6) для описания отношения (9.1) в явном виде.
Разделите все члены этого отношения на 2-DG и достигните предела как Dg — > 0: Я = 5 ^ (9.7) Поскольку выражение в фигурных скобках является производной произведения на r, выражение (9.7) можно переписать в следующем виде: A.(g₉.)= 5, g (9.8) Соотношение (9.8) является нормальным дифференциальным уравнением 1-го порядка для теплового потока. При объединении этого уравнения вы получите следующие результаты: ! ’- Т — +тк/, л⁾ Константа интегрирования должна быть установлена равной нулю. В противном случае граничные условия на оси проволоки не будут выполнены.
Движущаяся пластина может быть охлаждена до постоянной температуры в то времн как пластину 0 можно считать адиабатной по отношению к потоку тепла. Людмила Фирмаль
У меня есть| oo для r = 0(9.10) Итак, в конечном виде уравнение теплового потока выглядит следующим образом: Из уравнения (9.11) видно, что тепловой поток линейно возрастает с расстоянием от оси проволоки. При использовании закона Фурье теплопроводности[опорное уравнение (8.2)], подставляя в уравнение (9.11) q, значение-X (Г/ / , получаем дифференциальное уравнение температуры Γ. (9.12) Предположим, что теплопроводность X не зависит от температуры. Уравнение (9.12) легко интегрируется: — 5х» + С3(9.13) Мы также находим интегральную постоянную C2 из граничных условий.
Поверхность проволоки: Г =for для R = п (9.14) Из этого условия Cr = To +и распределение Окончательная форма деления (9.13) является: Соотношение(9.15) представляет собой параболический закон изменения температуры в поперечном сечении проволоки. Информацию о многих важных величинах можно получить из известных распределений температуры и теплового потока. 1) максимальное повышение температуры (r = 0): 2) повышение средней температуры: Так, в среднем температура повышается по сечению проволоки на величину, равную половине максимального повышения температуры.
Очевидно, что в рассматриваемом случае среднее увеличение — To равно среднему значению разности. 3)скорость тепловыделения на поверхности провода длины L: [г-н = 2nrr? Р | r_v = 2(9.18) В стационарном состоянии все тепло выделяется в процессе рассеивания электрической энергии、 Поверхность проволоки. При чтении материала, представленного в этом разделе, читателя, по-видимому, не покидает ощущение, что он уже все это знает, это ощущение вполне объяснимо, и жидкость течет по круглой трубе за счет того, что проблема нагрева проволоки имеет много общего с проблемой нагрева проволоки. viscosity. As вы можете видеть, таблица pz.
- Единственное различие между этими задачами-спецификация функции. Провод трубы Первая консолидация приводит к распределению 9 г Разделить значение T-To Результат 2-ой консолидации、 граничное условие для r = 0 ^ xn конечно. Параметры, характеризующие транспорт вт — — — го=о Источник питания (Po-Pb) / b 5、 Предположим, что p = const1 X, A,= const1 Поэтому до тех пор, пока не будет уточнена характеристика величин, обе задачи математически полностью эквивалентны. То есть она описывается теми же дифференциальными уравнениями и граничными условиями. Физические процессы, описываемые одними и теми же уравнениями и граничными условиями, обычно называют аналогичными процессами.
Конечно, не все задачи переноса импульса аналогичны задачам переноса энергии и массы. Однако, если такое сходство будет найдено, то рассмотрение транспортной проблемы значительно усложнится. simplified. So например, читателю нетрудно выявить аналоги вязких течений в кольцевом канале в вопросе молекулярной теплопередачи, и если такие аналоги найдены, то можно написать решение задачи теплопередачи.
Пространство между двумя пластинами заполнено жидкостью, и мы рассматриваем поток на достаточном расстоянии от входа, так что его можно считать полностью установившимся. Людмила Фирмаль
В электротехнической промышленности можно столкнуться со многими проблемами, связанными с теплопроводностью[1].Уменьшение скачка температуры внутри электропроводящих частей электрической машины может значительно продлить срок службы изоляционного материала. Для этого, например, в генераторе с очень большой мощностью(до 500 000 кВт) внутренние части статора охлаждаются с помощью liquid. In для того, чтобы более четко описать природу электрического нагрева, описаны 2 примера явлений, связанных с нагревательными проводами below. In в первом примере оценивается порядок теплового эффекта, во втором — метод учета температурной зависимости. Пример 9-1.
Из формул (9.3) и (9.16): 4М ровода электрп -.Температура поверхности (9.19) Плотность тока Следующим образом Связанный На конце провода длины b напряжение E (9.20 утра)) Откуда (9.22) В разделе 8.5 показана связь между K и A. Это решение определяется числом Лоренца A /AeT₀.Так обстоит дело с медью、 2.23-10 «в V’ — K»*. таким образом, напряжение, необходимое для повышения температуры основного провода на 10°C, будет: Е=2 ′ у2.23•10-2 / 29310 = 5000(1.49•10- 54.1 = 40 V (9.23)) Пример 9-2.
Проводимость и теплопроводность по отношению к температуре в EL1.Проводимость и проводимость В предположении, что температурная функция в виде разложения ниже 1: — ^- =1-016-И202 — (9.26) / -*,(р) -^ Бродячий (Т-т.) / т тоже Неоднородной электропроводностью л » т).Таким образом, плотность m является координатой r. (9.27> Безразмерный 。 ^ oH2yy HOL2To Безразмерная температура Безразмерной радиальной координаты Нчкцц, находим: Умножим обе 9.32) складка кровати Это функция.
Это просто формула(9.15). Решая это уравнение, мы находим 0 для E = 0 и инвертируем€ Характеристика источника тепла, формула (9.33), должна иметь решение, определенное формулой (9.35).Для сильных s Мы предполагаем, что распределение температуры может быть выражено в виде безразмерной прочности B. 0 = 4-(1-g1) (1 +В61+В20₂±••) Щенки? Дифференциальный О(б») указывает для Б Для материалов, свойства которых описаны Видеманом-Францем-Лоренцем (см. раздел 8.5), отношение n температура. Таким образом, соотношение Используя это и разложение(9.24) и (9.25), можно увидеть следующее: (1 _»03 )=(1 p_02-)(1 + 0) (9.39) Выравнивание То же. «!
Смотрите также:

