Оглавление:



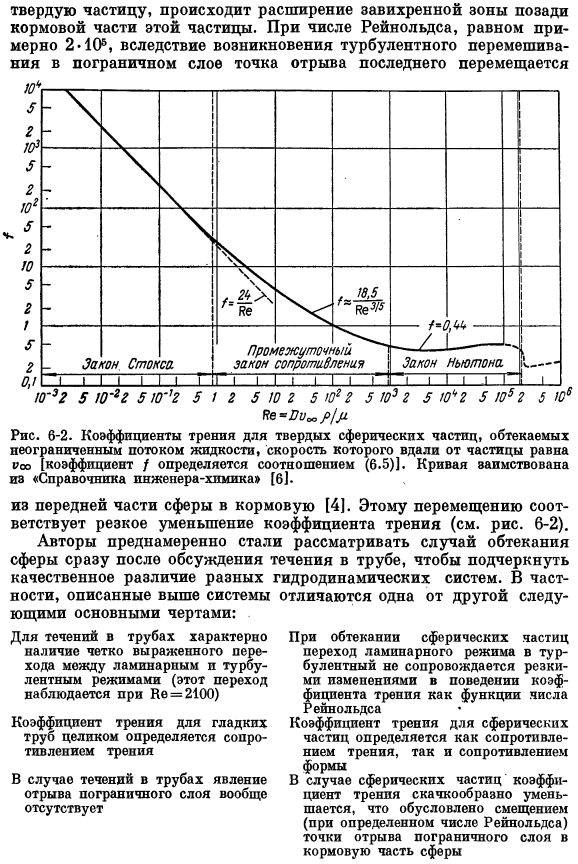



Коэффициенты трения для потоков, обтекающих сферические частицы
- В этом разделе, основанном на размерном анализе, описаны факторы, от которых зависит коэффициент трения при обтекании твердых сферических частиц. Кроме того, определение (6.5) используется для коэффициента трения. То же, что и раньше в рассуждениях предполагается, что плотность жидкости p постоянна. Обзор проводится в системе координат, описанной в разделе 2.6. Опишите формулу для динамической силы Pk, действующей на неподвижную твердую частицу со стороны жидкости, движущейся в положительном направлении оси 2. Эта сила равна разности между суммарной силой P = Pn -| — P и статической силой P.
ПК =(РП-П)+ П Сила Pn, P и P являются уравнениями Где p₀-давление жидкости на уровне r = 0 (то есть в плоскости, проходящей через экватор твердой частицы). Согласно определению (6.5), коэффициент трения/также может быть представлен в виде суммы 2 вкладов. / = / Форма+ АП(6.37) Используя выражение (6.34)-(6.36), вклады/ format и / tr могут быть записаны в явном виде.
Так как физические параметры топочных газов незначительно отличаются от параметров воздуха, то все расчеты можно производить, применяя физические параметры воздуха. Людмила Фирмаль
В Формуле (6.38)-(6.39), используются следующие безразмерные переменные: Рейнольдс (6.44) Для вычисления коэффициентов/ необходимо знать зависимость величин P*, V *и r> 0 от r*, 0 и в разделах 2.6 и 4.2 мы показали, как выражение закона Стокса может быть найдено в условиях «ползучего течения», то есть очень медленных течений вокруг сферы, число Рейнольдса которой не превышает 0,1. При Be> 0,1 точная аналитическая формула для профиля с пониженной скоростью и давлением не может быть получена.
Однако известно, что для несжимаемых жидкостей такие профили могут быть рассчитаны в принципе по формулам (3.109) и (3.110)*.Эти уравнения должны быть решены со следующими граничными условиями: если r * = 1 [=0 (6.45 )) (6.46) Р ’= 0(6.47) Поскольку граничные условия не вводят в задачу дополнительных безразмерных групп, решения системы уравнений (3.109) и (3.110) имеют вид: Р * = р *(х, г *, р *он) (6.48) р * = ₀ *(х*, г*,», он)(6.49) А также при рассмотрении течения в трубопроводе и дальнейшем обсуждении(раздел 6. 2), можно сделать вывод, что коэффициент трения должен удовлетворять соотношению функций/ = / (Be) (6. 50).
Таким образом, анализ размеров системы уравнений в частных производных, описывающих течение несжимаемой жидкости вблизи твердых сферических частиц, и определение коэффициента трения, показывает, что величина/является лишь функцией числа Рейнольдса. На рис. 6-2 представлен график зависимости коэффициента трения от числа Рейнольдса. Этот график основан на ряде экспериментальных данных по гидродинамике потоков, обтекающих гладкие сферические частицы.6-2, как видно из рисунка, для течения вблизи сферы нет резкого перехода от неустойчивого ламинарного течения к турбулентному state. In в отличие от случая течения в трубе, указанный скачкообразный переход наблюдается при he = 2100.
С увеличением скорости потока *Для этой системы (6.44 а). Уравнение Твердые частицы, зона закручивания, расширяются за кормой этой частицы. Когда число Рейнольдса составляет приблизительно 2-10, когда из-за появления турбулентного перемешивания От передней части сферы до кормы[4].Это движение соответствует резкому уменьшению коэффициента трения (см. рис. 6-2). Чтобы подчеркнуть качественное различие между различными гидродинамическими системами, авторы начали целенаправленно рассматривать случай обтекания сферы сразу после обсуждения течения в ней. pipe.
- В частности, вышеуказанные системы отличаются друг от друга. В случае течения в трубе, как правило, явление разделения пограничного слоя Недостающий Читатель должен быть знаком с общим видом кривых, показанных на рисунке. 6-1 и 6-2. В диапазоне чисел Рейнольдса, соответствующем режиму»ползучего течения«, сопротивление определяется законом Стокса, как описано выше.
Этот закон может быть выведен теоретически путем решения уравнения движения и уравнения непрерывности аналитически (в рамках приближений, где член уравнения движения (3.29) может быть опущен).Приведя формулу Закона Стокса, преобразовав эталонную формулу (2.107) 1 в форму (6.5), получим следующее соотношение: Итак, когда он обтекает сферические частицы в условиях «ползучего течения», закон сопротивления выглядит так: В логарифмических координатах этот закон выражается в виде прямой линии. Для более высоких чисел Рейнольдса чисто теоретические вычисления очень утомительны.
Вследствие большого значения коэффициента теплообмена со стороны, омываемой водой, и высокой теплопроводности стенок труб температура внешней поверхности труб лишь слегка выше температуры пара. Людмила Фирмаль
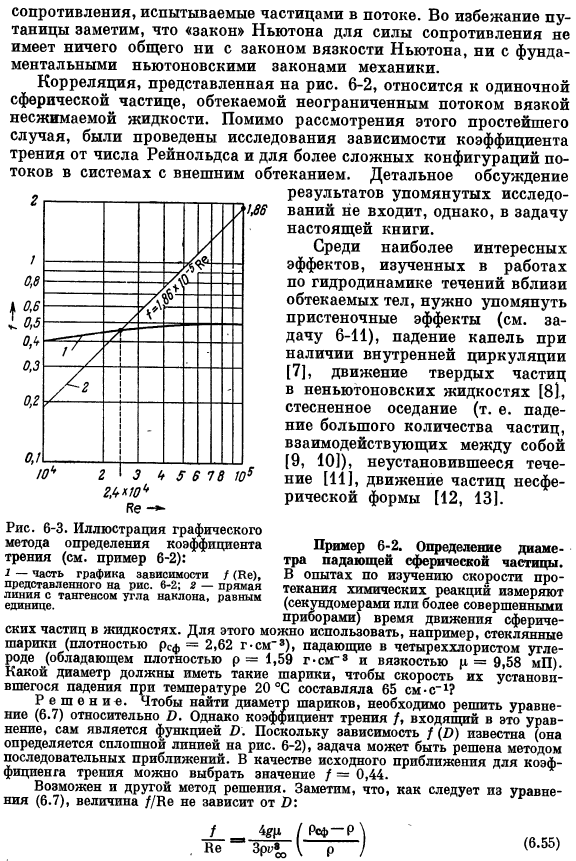
Некоторым исследователям, приложив большие усилия, удалось найти значение Be = 10/.Но часть кривой/ = / (Be) соответствует Be> 0.1.Если число Рейнольдса велико, то для корреляции экспериментальных результатов можно использовать простую аналитическую формулу. Поэтому в средней области чисел Рейнольдса выполняется следующая приближенная зависимость. 2 менее 500 ′* (6.53) Из уравнения (6.53), особенно для Be> 2, зависимость коэффициента трения от числа Рейнольдса слабее, чем предсказывает закон Стокса. При Be 2 уравнение Стокса представляет экспериментальные данные более точно, чем уравнение (6.53).
В области 500 Be 2•10⁶ коэффициент трения очень слабо зависит от числа Рейнольдса, поэтому его можно считать постоянным в первом приближении. / −0.44 500 Be 2-10⁵ (6.54) В этой области, обычно называемой диапазоном закона Ньютона, сила сопротивления приблизительно пропорциональна квадрату скорости потока, входящего в частицу. Используя соединение(6.54), вы можете быстро оценить мощность Сопротивление, которое частицы в потоке receive. To во избежание путаницы следует отметить, что ньютоновский «закон» сопротивления не имеет ничего общего с ньютоновским законом вязкости или законами основной ньютоновской механики.
Корреляция 6-2, показанная на рисунке, относится к одной сферической частице, обтекаемой неограниченным потоком вязкой несжимаемой жидкости. fluid. In кроме изучения этого простейшего случая, было проведено исследование зависимости коэффициента трения от числа Рейнольдса для более сложной конфигурации течения систем с внешним потоком. Однако, подробное обсуждение результатов этих исследований не входит в эту задачу kupigi. К числу наиболее интересных эффектов, изучаемых при изучении гидродинамики течений вблизи жидких тел, относятся эффекты, близкие к стенкам (см.
Задачу 6-11, падение капель при наличии внутренней циркуляции[7].Движение твердых частиц в неньютоновских жидкостях, движение связанных твердых тел в неньютоновской жидкости(т. е. движение большого числа взаимодействующих частиц [9,101], движение твердых тел в неньютоновской жидкости.
Смотрите также:
| Определенно коэффициентов трения | Коэффициенты трения для насадочных колонн |
| Коэффициенты трения для течений в трубах | Межфазный перенос в изотермических системах. Задачи |

