Методические указания по теплотехнике

Теплота передается через ограждающие конструкции помещений, а также во всех непрерывно действующих нагревательных приборах — котлах, печах, водо- и воздухоподогревателях, сушилках, пропарочных камерах и других теплообменниках.

Расчет теплопередачи заключается обычно в определении количества теплоты, которая передается в единицу времени между теплоносителями через стенку, разделяющую их.

Может рассматриваться и обратная задача — определение требуемой площади поверхности стенки между жидкостями для передачи заданного количества теплоты от горячего теплоносителя к холодному.

Попутно с этими основными задачами при конструировании ограждений, разделяющих горячую и холодную жидкости (стенки печей, барабанов, кипятильных труб котла и т. п.), рассчитывают температуры на поверхности каждого слоя ограждения, с тем чтобы рабочая температура материала не превышала максимально допустимое для него значение.

В настоящей главе рассматривается теплопередача через плоскую, цилиндрическую, сферическую и ребристую стенки для условий стационарного режима, а также методика расчета теплообменных аппаратов.

Возможно эта страница вам будет полезна:

Предмет теплотехника

Теплопередача через плоскую стенку

Теплота передается от горячей жидкости с температурой 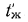к холодной жидкости, имеющей температуру 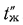, через плоскую однородную стенку с теплопроводностью .

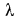Стенка имеет толщину 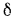, которая значительно меньше линейных размеров ее площади поверхности S, что дает возможность пренебречь потерями теплоты с торцов стенки. Значения коэффициентов теплоотдачи, определяемые условиями движения жидкостей, считаем известными и соответственно равными на горячей стороне 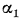и на холодной ,.

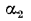Температуры поверхностей стенки неизвестны. Обозначим их соответственно через 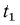и 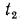°С (рис. 16.1, а). Требуется определить плотность теплового потока, проходящего через стенку, и распределение температур в стенке. В условиях стационарного режима вся теплота, передаваемая горячей жидкостью стенке, проходит через нее и поглощается холодной средой. При этом плотность теплового потока q может быть выражена равенствами:

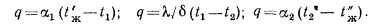
Из этих равенств определяем разности температур:

и, складывая их, получаем

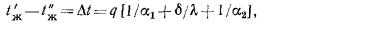
откуда искомая величина

а тепловой поток

где

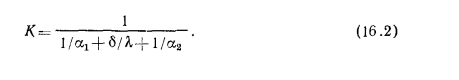
Коэффициент К носит название коэффициента теплопередачи. Он имеет ту же размерность, что и 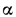; числовое значение его определяет мощность теплового потока, проходящего от одного теплоносителя к другому через единицу поверхности стенки, разделяющей эти теплоносители, при разности температур между ними 1°.

В знаменателе формулы (16.2) слагаемое 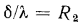представляет собой термическое сопротивление теплопроводности (см. § 13.2), а слагаемые 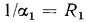и — термические сопротивления теплоотдачи (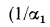 — от горячей жидкости к стенке, а 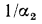— от стенки к холодной жидкости). Сумма термических сопротивлений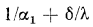 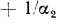, представляющая собой величину, обратную коэффициенту теплопередачи, называется термическим сопротивлением теплопередачи и обозначается R, т. е.

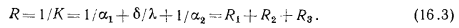
Единицами измерения для К и R служат соответственно 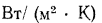и .

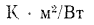Для плоской стенки, состоящей из нескольких слоев толщиной 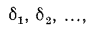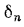с соответствующими теплопроводностями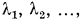 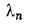, термическое сопротивление теплопередачи составит

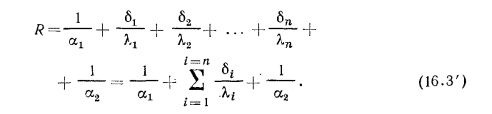
В этом случае выражение (16.2) для коэффициента теплопередачи К принимает вид

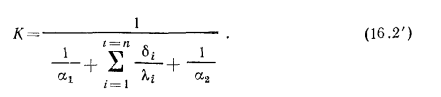
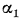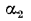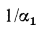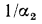Из формулы видно, что величина К всегда меньше каждой из величин и и если термические сопротивления слоев стенок малы по сравнению с и , то

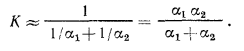
Полученное равенство показывает, что наибольшее влияние на К оказывает тот коэффициент теплоотдачи, который значительно меньше другого: например, при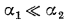

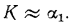
Для определения температуры 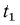и 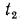на поверхностях стенки достаточно подставить найденное значение плотности теплового потока q в равенство (а), тогда:

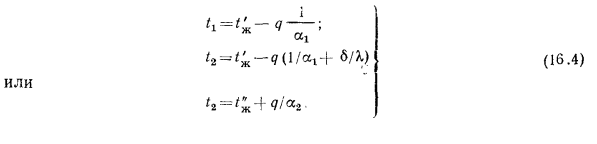
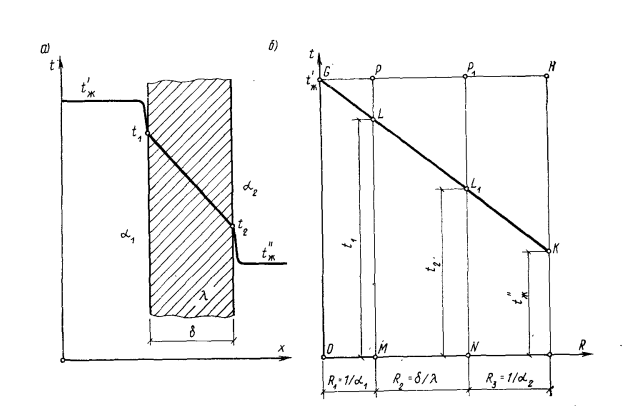
Графический способ определения температур

Эти температуры можно также определить графическим способом (рис. 16.1, б), суть которого состоит в том, что но оси абсцисс в одном масштабе откладывают последовательно все термические сопротивления, а на крайних ординатах от произвольного нуля откладывают температуры 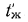и .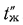

Соединяя полученные точки прямой линией GК , получаем в точке пересечения ее с остальными ординатами температуры на поверхностях слоев стенк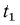и и 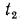. Из рассмотрения подобия треугольников, например треугольников GPL и GHK, следует, что

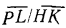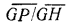=, откуда

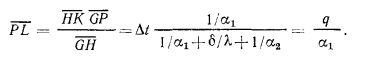
Согласно уравнению (16.4), 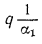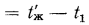следовательно, отрезок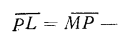 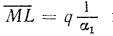или 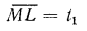. Аналогично из подобия треугольников 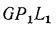и GHK доказывается, что отрезок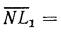

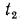
Возможно эта страница вам будет полезна:

Решение задач по теплотехнике

Теплопередача через цилиндрическую стенку

Мощность теплового потока, передаваемого от горячей жидкости к холодной через цилиндрическую стенку, находят по той же методике, что и для плоской стенки.

Пусть внутри трубы, диаметр которой достаточно мал по сравнению с ее длиной (это позволяет пренебречь потерями теплоты через торцы стенки), протекает горячая жидкость с постоянной температурой 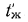— Снаружи трубы находится холодная среда, температура которой также неизменна и равна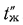. Стенка грубы однородна, ее теплопроводность равна 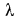, внутренний диаметр 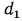наружный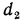

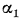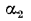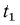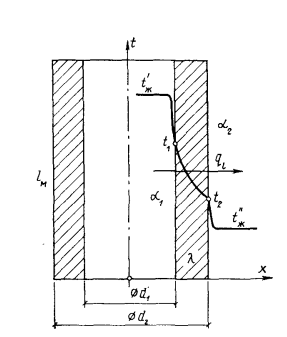
Суммарные коэффициенты теплоотдачи соответственно равны и . Неизвестные температуры на внутренней поверхности стенки обозначим и на наружной 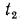(рис. 16.2). В условиях стационарного режима линейная плотность теплового потока, т. е. количество теплоты, переданной от нагретой среды стенке, прошедшего через стенку и. переданного от стенки к более холодной среде, будет постоянным и соответственно равным:

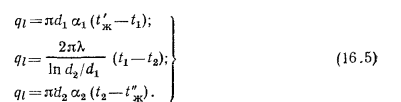
Определяя по этим уравнениям разности температур:

и суммируя, можем написать

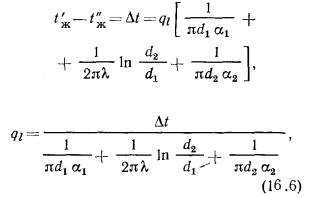
или

где

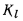— линейный коэффициент теплопередачи, числовое значение которого определяет мощность теплового потока , проходящего от одного теплоносителя к другому через 1 м длинны трубы при разности температур между теплоносителями, равной 1°.

Величину 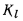находят по формуле

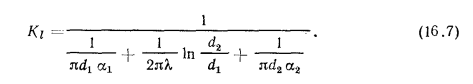
Мощность теплового потока, переданного через трубу длиной l, составляет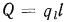

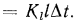
Величина, обратная линейному коэффициенту теплопередачи, называется линейным термическим сопротивлением теплопередачи, т. е.

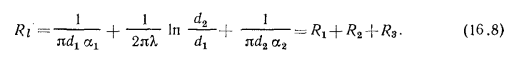
В этом уравнении среднее слагаемое 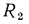является термическим сопротивлением теплопроводности стенки (см. § 13.2), а крайние слагаемые и 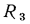— термическими сопротивлениями теплоотдачи от горячей жидкости к внутренней поверхности цилиндрической стенки и от наружной поверхности к холодной жидкости.

Единица измерения линейного коэффициента теплопередачи

Единица измерения линейного коэффициента теплопередачи — 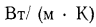, единица измерения линейного термического сопротивления теплопередачи — м • К/Вт.

Для многослойной цилиндрической стенки в состав выражения для вычисления линейного термического сопротивления 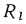вместо одного слагаемого, определяющего сопротивление теплопроводности стенки,

должен входить ряд однотипных слагаемых в соответствии с числом слоев, т. е.

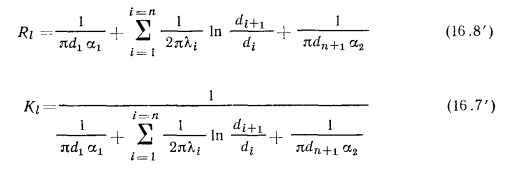
Неизвестные значения температур поверхностей стенк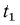и и 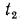находят из равенств (б), если подставить в них полученное значение по уравнению (16.6). Решая эти равенства, можем написать:

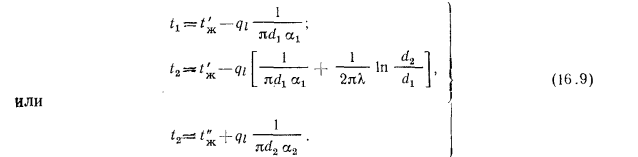
Температуры между слоями у многослойной цилиндрической стенки могут быть определены или графическим способом аналогично определению температур у плоской многослойной стенки, или аналитическим путем, рассмотренным.

Плотность теплового потока, отнесенного к внутренней или наружной поверхности трубы, определяется по известным соотношениям:

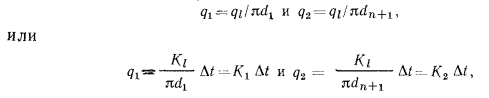
где — коэффициенты теплопередачи цилиндрической стенки, отнесенные соответственно к единице внутренней или наружной ее поверхности, определяемые по формулам:

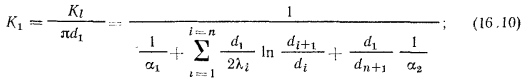
dn+1 1 lyn dn+1 di+l

При 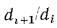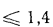в соответствии с уравнением (13.12′)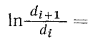 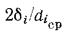, что позволяет упростить расчетные формулы, которые, например, для 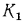и принимают вид:

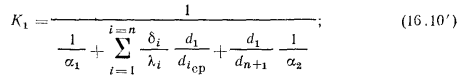
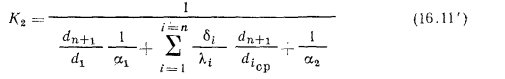
В случае использования тонких цилиндрических стенок значения 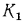и определяют по тем же уравнениям, что и для плоской многослойной стенки формула (16.2), так как отношения 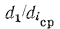и 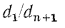практически можно принять равными единице.

Этим, в частности, объясняется то положение, что при расчете теплообменных аппаратов, имеющих обычно трубчатую конструкцию (конденсаторы, котлы, подогреватели), теоретический коэффициент теплопередачи рассчитывают по формуле для плоской многослойной стенки.

Рассмотрим более подробно формулу (16.8), определяющую линейное термическое сопротивление теплопередачи трубы. Из этой формулы следует, что с увеличением наружного диаметра трубы 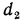возрастает термическое сопротивление теплопроводности стенки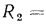 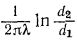и уменьшается термическое сопротивление теплоотдачи от стенки к холодной жидкости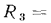 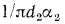. Поэтому в зависимости от толщины стенки трубы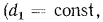 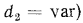ее термическое сопротивление теплопередаче будет увеличиваться или уменьшаться.

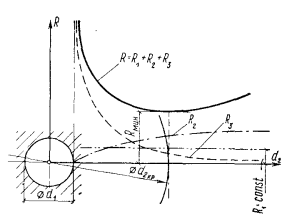
• Из рис. 16.3 видно, что при определенном значении 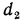, называемом критическим, термическое сопротивление стенки трубы R будет иметь минимальное значение, и количество теплоты, передаваемой в этом случае от внутренней среды к наружной, будет максимальным. Величину 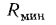легко определить математическим путем.

Для этого нужно взять производную термического сопротивления грубы при переменном 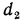и приравнять ее к нулю. В результате получим:

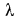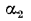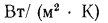
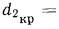
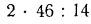
Исследование полученной формулы показывает, что, например, для стальной трубы при = 46 Вт/ (м • К) и = 14 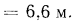Таким образом, предельное значение диаметра металлических труб, после увеличения которого количество передаваемой через трубу теплоты

будет падать, весьма велико и измеряется метрами. В границах этого диаметра чем толще стенка металлической трубы, тем больше теплоты через нее будет передаваться от горячей жидкости к холодной. Если труба изготовлена из теплоизоляционного материала, например асбестовой массы с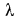 = 0,167 Вт/ (м • К ), то при том же значении 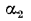= 14 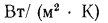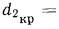2 • 0,167 : 14 = 0,024 м, т. е. для труб с наружным диаметром более 24 мм при увеличении толщины изоляции теплопередача будет снижаться.

У бетонных труб при 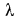= 1,17Вт/ (м • К) и 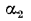=14 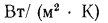) 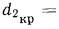160 мм. При наружных диаметрах этих труб, которые меньше или больше 160 мм, количество теплоты, передаваемой от внутренней ■среды к наружной, снижается.

Это означает, что если металлическую трубу покрыть слоем бетона, теплопередача через такую двухслойную цилиндрическую стенку может оказаться больше, чем через чистую металлическую трубу.

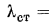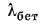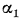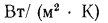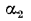Действительно, если наружный диаметр стальной трубы принять равным 40 мм, толщину ее стенки 2 мм, а наружный диаметр бетонной рубашки на этой трубе 120 мм, то при 46 Вт/ (м • К), = 1,17 Вт/ (м • К), = 2800 и = 14 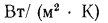термическое сопротивление чистой металлической трубы составит

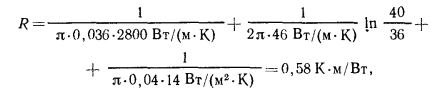
а трубы с бетонной рубашкой —

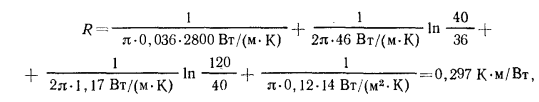
т. е. почти в 2 раза меньше, чем стальной трубы без слоя бетона. Это свидетельствует о том, что при диаметре цилиндрической оболочки меньше 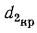тепловая изоляция теряет свою роль.

Поэтому при конструировании нагревательных приборов целесообразно использовать бетон, а также керамику для частичной замены металла.

В частности, в промышленности строительных материалов широкое применение находят керамические рекуператоры, состоящие из блоков различного фасонного сечения, образующих при укладке взаимно перекрещивающиеся каналы, по одной стороне которых движется воздух, подругой — продукты горения топлива.

Теплопередача через сферическую и ребристую стенки

При установившемся тепловом состоянии системы количество теплоты Q, переданной через однородную сферическую стенку от горячей жидкости к холодной, так же как количество теплоты, переданной плоской и цилиндрической стенками, может быть выражено тремя следующими уравнениями:

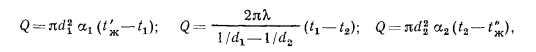
где 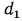, 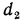— внутренний и наружный диаметры сферической стенки; 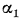, 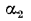— коэффициенты теплоотдачи от горячей жидкости к стенке и от стенки холодной жидкости; 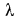— теплопроводность материала стенки; 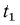, 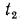— температуры поверхностей стенки.

Из этих уравнений определяют искомое значение

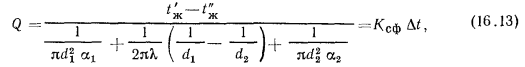
где 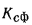— коэффициент теплопередачи для сферической стенки, равный:

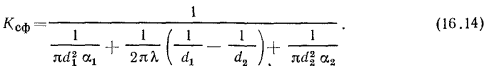
Величина, обратная 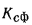называется термическим сопротивлением теплопередачи сферической стенки и выражается соотношением

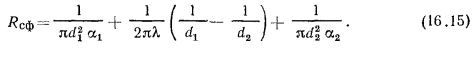
Единицей измерения для 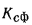служит Вт/К, для термического сопротивления теплопередачи сферической стенки — К/Вт.

Анализ формул (16.3), (16.8) и (16.15) для термических сопротивлений стенок различной конфигурации показывает, что чем больше площадь внешней поверхности стенки отличается от площади внутренней, тем меньше при прочих равных условиях термические сопротивления теплоотдачи таких стенок.

Например, у плоской стенки 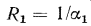у цилиндрической 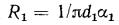а для сферической стенки 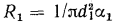. Поэтому для понижения термического сопротивления системы в целом достаточно увеличить площадь поверхности стенки, сделав ее ребристой с той стороны, где меньше теплоотдача.

Ребра увеличивают площадь поверхности теплообмена и таким образом при том же способствуют повышению количества передаваемой теплоты.

В последнем нетрудно убедиться, если проанализировать, как передается теплота через ребристую стенку (рис. 16.4).

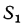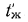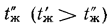Пусть площадь поверхности этой стенки с гладкой стороны с ребристой — , температуры жидкостей, омывающих стенку, и коэффициенты теплоотдач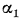и и 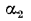при этом 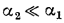, температуры поверхностей стенк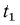и и 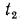теплопроводность стенки 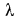, а ее толщина .

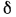Процесс передачи теплоты через стенку соответственно трем

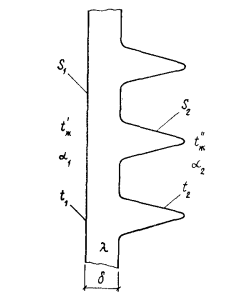
составляющим его звеньям может быть выражен следующими тремя уравнениями:

Q

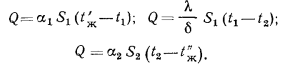
Решая эти уравнения относительно частных температурных напоров и складывая их, получим

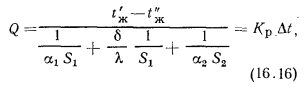
гдe Kp — коэффициент теплопередачи я ребристой стенки, равный:

При расчете плотности теплового потока на единицу гладкой поверхности стенки имеем

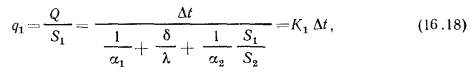
где — коэффициент теплопередачи, отнесенный к плоской поверхности ребристой стенки и равный:

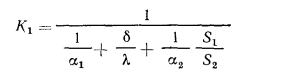
Если определяют тепловой поток на единицу ребристой поверхности стенки, то расчетная формула принимает вид

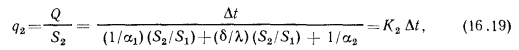
• где 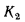— коэффициент теплопередачи, отнесенный к ребристой поверхности стенки и равный:

Расчет теплопередачи через тела неправильной формы можно приближенно сводить к трем рассмотренным случаям. С этой целью стенку сложного очертания мысленно деформируют, придавая ей правильную форму плоской стенки, цилиндра или шара в зависимости от того, к какому типу тел ее можно отнести.

При этом расчетную толщину такой деформированной стенки определяют из условия равенства ее объема и объема правильной стенки, а расчетный коэффициент теплоотдачи для поверхности деформированной стенки находят из равенства:

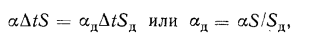
где индекс «д» относится к деформированной стенке, а величины без индекса характеризуют стенку правильной формы.

Все приведенные формулы по расчету теплопередачи могут быть использованы и для расчета тепловой изоляции.

Для этого с учетом допустимых тепловых потерь объекта, возможности осуществления технологического процесса, а также соблюдения техники безопасности выбирают вид изоляции, температуру на ее поверхности и рассчитывают требуемую толщину слоя изоляции. Основные темы теории из учебников тут, надеюсь она вам поможет.

При выборе изоляции немаловажное значение имеют и такие факторы, как масса, гигиеничность, удобство монтажа и срок службы изоляции.