Оглавление:


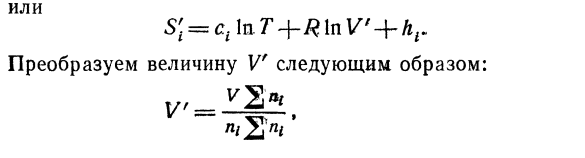


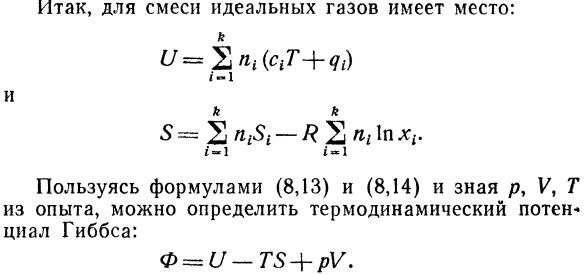

Внутренняя энергия и энтропия смеси идеальных газов.
- Внутренняя энергия и Энтропия смеси Идеальный газ. Принуждение Месса Идеально подходит для молекул 1g Внутренняя энергия газа UI ^ CiT, c% удельная теплоемкость V = const Сто восемьдесят девять Как количество: Эта формула действительна для: Физическое смешивание газов без химических реакций.
Таким образом, внутренняя энергия смешанного газа равна Людмила Фирмаль
Если Когда газы смешиваются между собой, происходит реакция 、 Внутренняя энергия смеси будет равна: ^ = ЕДГ + 2 взр.,, (8.13) Где PG означает количество молекул грамма Сырой газ и продукты реакции, а также qt-химия Химическая энергия выпущенная или поглощенная в 1 месяце Молитесь в присутствии реакции. 19) написание формулы энтропии идеального газа В переменной 7, V для 1 моля V-го компонента
Смесь: Где: Hi = CI в Определяет значение энтропии для одного и того же компонента После смешивания. Каждый газ после смешивать、 Контейнер U, и молекулы 1g каждого газа в Объем V — уменьшается. Вы Адиабатическим расширением энтро、 Энтропия газа С2、 Энтропия Si перед разложением на Это выражение можно использовать для написания выражения Выражение энтропии 1 моль для каждого последующего компонента
- Смесь: Или Преобразуйте значение Vf в: Сто девяносто RU В это число молей всех газов в системе. ^ ^Значение Г » — ^представляет собой объем молекулы 1 грамм Газ при определенной температуре и определенном давлении отношения-младший? = Xi-концентрация газа. Отсюда Затем выражение S принимает следующий вид: Ы ’ т = ЧВ НТ + Р \ НВ-Rxxxi + привет. (8.13 ’) В выражении (8.13′) первые 2 члена и последний
Термин справа от суммы-это значение энтропии Blend. So … Следовательно, энтропия всей смеси Или С = 2 * а-#с * * lnjc,. (8.14) — Р 2 х в XP Но с тех пор Тогда 1px < < 0, то есть в результате смешения газов, энтропия Система растет. Этого и следовало ожидать. Как смешивание газов является процессом изоляции
Энтропии после смешения газ Людмила Фирмаль
Это сопровождается увеличением энтропии. Формула с, 14) является так называемой Парадокс Гиббса. Это выражение является В принципе、 Любой газ. Однако, 2 одинаковых В этом случае, как видно из Формулы (8.14), газ、 Энтропия такой системы остается неизменной. В Итак, об идеальной смеси газов можно сказать следующее: КК. о = ^ 2Д ^ я ^ я-* \ 2У т ^ я * П%Л * Используйте формулы (8.13) и (8.14) и знайте p, V, T По опыту можно определить термодинамический потенциал Гиббс СИАР.: 0 ^ U-TS + pV.
Смотрите также:
Решение задач по термодинамике
| Правило фаз Гиббса. | Закон действующих масс. |
| Общие условия равновесия в гомогенной системе. | Растворы и смеси. Условия равновесия разбавленных и идеальных растворов. |

