Оглавление:




Установившееся двухмерное вязкое течение. Функция тока
- Задачи, рассмотренные в главах 2, 3 и разделе 4.1, были выбраны таким образом, чтобы все элементы скорости, кроме 1, исчезли. Полное системное решение Навье-уравнения Стокса для течения в 2-и 3-направлениях чревато большими. В большинстве случаев решение этих задач требует специального метода. Однако в некоторых классах потоков с постоянными p и p дифференциальные уравнения можно несколько упростить, описывая их на основе функции потока φ.
Чем более точно уравнение описывает фактическое изменение свойств, тем больше оно будет содержать постоянных величин и тем больше параметров появляется в безразмерных уравнениях, описывающих поток и теплообмен. Людмила Фирмаль
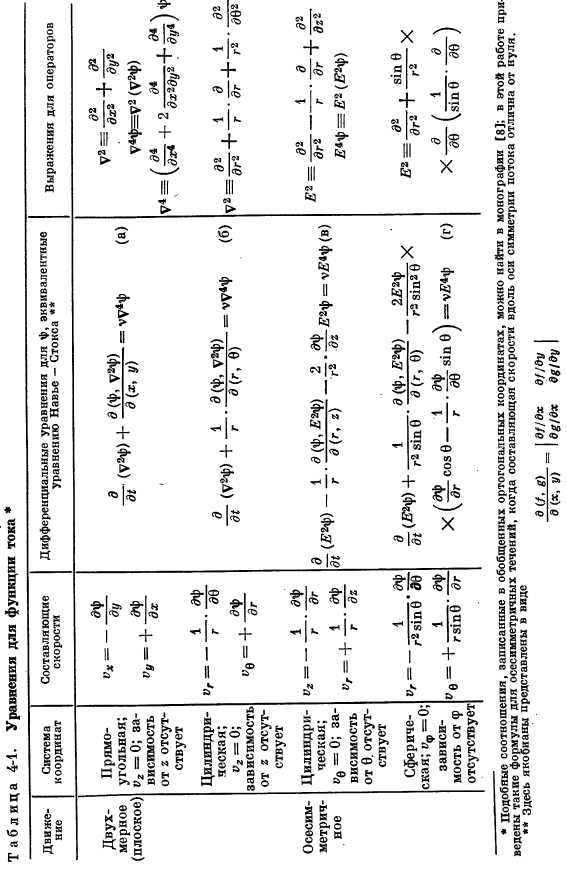
Компоненты скорости представлены производной φ (таблица 4-1), так что уравнение неразрывности заполняется автоматически. Затем вы можете объединить 2 непустых компонента уравнения движения, чтобы исключить член, содержащий компонент P. Эта процедура дает скалярное дифференциальное уравнение 4-го порядка для φ.In стол. На рис. 4-1 приведены уравнения, соответствующие некоторым наиболее важным случаям течения*.Физическое значение текущей функции таково, что линия φ= const1 представляет собой поток line. In при устойчивом течении обтекаемая линия совпадает с траекторией движения частицы жидкости.
- Уравнения движения. Соответствующее вычисление дает закон Стокса. Это было кратко объяснено в разделе 2.6. 8) / «/ / потребления» / / в » I О (х, г) я чч / AX в / / ой и Эта задача была выбрана потому, что она интересна с точки зрения проведения технологических процессов, связанных с движением твердых частиц и капель. Идеальный поток жидкости вокруг сферы обсуждается в выпуске 4-6.Решение этой проблемы и следующие решения являются 2 наиболее важными из них. В этом разделе в качестве примера рассматривается стационарное течение вязкой жидкости вокруг сферы. Такое решение справедливо только для течений ползучести, которые могут игнорировать инерционный член
Однако температуры здесь не могут отсчитываться от какой-то произвольной начальной, так как в предыдущих уравнениях появляется абсолютная температура. Людмила Фирмаль
Координирует уравнение (4.42) должно быть решено со следующими граничными условиями: (4.46) Подставляя эту формулу в Формулу (4.42), получаем: Тестовое решение однородного уравнения 4-го порядка вида f ®= C r означает, что n может принимать значения −1, 1, 2 и 4.So функция I ® выглядит следующим образом: (4.48) * Приведенный здесь лосьон следует тому, что описано в монографии[9].Другие приближения описаны в этой работе[1]. Мед Компонент скорости (см. таблицу 4-1) эквивалентен: (4.54) Метод, который характеризуется уравнением (4.54), ранее использовался для исследования течения непиотонической жидкости Слейтером [10].
Смотрите также:
| Исследование уравнений сохранения методами теории подобия и анализа размерностей. Задачи | Установившееся двухмерное потенциальное течение |
| Неустановившееся вязкое течение | Теория пограничного слоя |

