Оглавление:




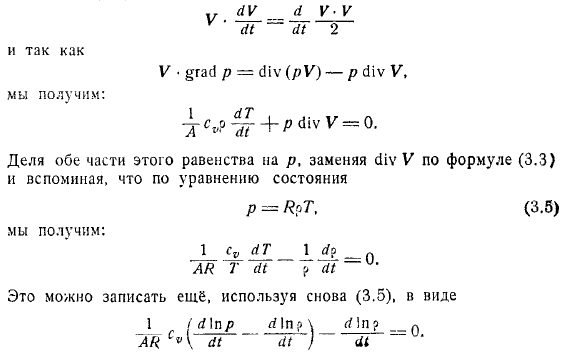


Уравнения газовой динамики в дифференциальной форме
Для тех участков жидкости, где гидродинамические элементы и их первые производные остаются непрерывными, можно записать уравнение в дифференциальной форме. Уравнения движения выводятся подробно уже с начала. To получив эти уравнения, сначала разделим обе части на разности, а затем, приняв ее, перейдем к пределу.
Очевидно получение. Поскольку решение задач по гидромеханике и сам объем зависит от времени, нельзя вводить производную слева под знаком интеграла, но можно написать. Ввод лагранжевых координат. Где положение объема в данный момент находится в Лагранжевых координатах и является функциональным определителем.
- С другой стороны сильные разрывы, из уравнения неразрывности. Подобный этому Отмечая, что они независимы от времени, от их определений, мы можем написать.
- Вернитесь к старой переменной, наконец. Затем переведите правильный интеграл в интеграл объема по формуле Грина и перенесите все под знаком интеграла объема.
С готовностью объема и предполагаемой непрерывностью подынтегрального выражения вы получаете. Людмила Фирмаль
Если объемная сила отбрасывается, это соответствует формуле в части. Уравнение неразрывности было выведено подробно в первой части.
Для сжимаемых жидкостей. Наконец, уравнение энергии делит обе его части на предел, и когда оно достигает предела, то после сбора членов оно выглядит так. Слева от этого уравнения примените преобразование, аналогичное тому, которое применяется для вывода уравнения.
- Преобразуйте левую сторону в интеграл объема по зеленой формуле, перенесите все в одном направлении и соберите под целым знаком.
- И для объема семантики и непрерывности подынтегрального выражения. Затем умножьте обе стороны уравнения на скаляр и вычтите из него.
Если мы разделим обе стороны этого равенства, замените его выражением и вспомните его уравнением состояния. Это может быть использовано снова в форме и написано снова. Сбор производных для членов.
С помощью простого преобразования, конечный результат. Людмила Фирмаль
Коэффициент теплоемкости. Это выглядит как «уравнение теплопритока» — условие теплоизоляции в дифференциальной форме.
Обратите внимание, что их всегда больше одного. Для одноатомного газа. Для атомарного газа (при комнатной температуре). В случае воздуха, он заглатывается чаще. При выводе уравнений этого раздела мы исходили из того, что гидродинамические элементы и их производные непрерывны.
Теперь предположим, что существует поверхность уравнений газовой динамики, которая является слабой разрывной поверхностью, и сама функция непрерывна везде, но уже первая производная о координатах и времени подвергается при прохождении через разрыв. Такой слабый разрыв, как мы увидим позже, возможен для нестационарных и широких разновидностей стационарного движения. Давайте более подробно рассмотрим этот вопрос.

