Оглавление:






Уравнение движения
- Аналогично вышесказанному, мы описываем баланс импульса объемного элемента Ah Du Ah в виде корреляции. Легко видеть, что уравнение (3.10) является лишь обобщением соотношения (2.1). В случае нестационарных течений. Общий поток выходных данных примерно такой же, как и в главе 2. Однако для учета нестационарности необходимо проанализировать движение жидкости через все 6 плоскостей объемного элемента в любом направлении(см. раздел 3.1). Уравнение (3.10) подчеркивает, что это векторное уравнение, которое может быть описано компонент за компонентом для всех 3 осей x, y и 2. Для простоты мы опишем компонент x каждого члена в уравнении (3.10). Компоненты y и 2 могут быть записаны по аналогии.
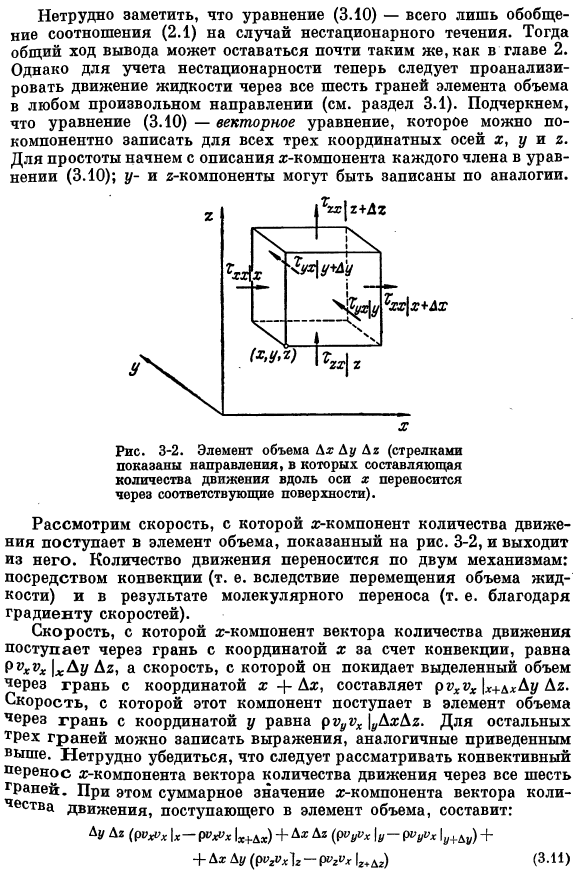
Стрелки имеют компонент оси x Рассмотрим скорость, с которой компонент импульса X входит в элемент объема, показанный на рисунке 3. 3-2, и оставьте его. Импульс передается двумя механизмами: конвекцией(то есть движением объема жидкости) и результатом молекулярного переноса (то есть градиентом скорости). Для конвекции скорость, с которой компонент X вектора импульса входит от грани координаты x, равна| xDu Dg, а скорость, с которой он выходит из выбранного объема через грань координаты x + Ax, равна pg>₁rxrx|x DL DlDu Dg.
Когда критерий Рейнольдса имеет одну и ту же величину в обоих случаях, тогда в одинаково расположенных точках (с одними и теми же безразмерными координатами) безразмерные скорости и давления будут иметь одинаковые величины в области вокруг цилиндров 1 и 2. Людмила Фирмаль
Скорость, с которой этот компонент входит в элемент объема из координатной плоскости y, равна p oooh | rDhD2.Для остальных 3 граней можно создать выражение, подобное приведенному выше. Легко видеть, что конвективный перенос x-компонента вектора импульса через все 6 граней должен быть considered. In в этом случае сумма x-компонента вектора импульса, входящего в элемент объема, равна: Д «ДХ (Р»Л | Х — ЛП | хп)+ топор ((Р> Ш \ Г-(я> У1> х 1^^) + Аналогично, скорость, с которой компонент X вектора импульса молекулярным движением перемещается в управляющий объем через плоскость с координатой x, равна t» / xDuDx, а скорость, с которой плоскость выходит с координатой x + Dx, равна / x₊dhDu yes.
Скорость прихода компонента x, проходящего через плоскость координаты y, равна|ДДДз. Аналогичные выражения могут быть написаны и для других 3-х граней (см. рис. 3-2).Заметим, что Xuh-это поток компонента x, проходящий через плоскость, перпендикулярную оси Y. Если суммировать все 6 компонентов по молекулярному переносу, то получится: ДУДх(Тхх|х-Тхх1″^)+Д*Дх(Тцх1а-трх1^) +Д»ДУ(т»|г-т» 1 ^)(3.12) Как упоминалось выше, эти импульсные потоки можно рассматривать как напряжение.
Таким образом, величина xxx-это нормальное напряжение участка, перпендикулярного оси x, а xih-тангенциальное (или тангенциальное) напряжение, возникающее на плоскости координаты y под действием силы вязкого трения.、 вдоль оси X. Что касается питания, то в большинстве случаев самое главное В результате под давлением Ясно, что результирующая сила жидкости p на единицу массы и сила, указанная в направлении силы тяжести x, равна: Ду д «(р | х-П |₍МДВ)+ pUhD » Ду Д » (3.13) Давление движущейся жидкости определяется уравнением состояния p = p(p, T), которое является скалярной величиной. Наконец, кумулятивная скорость x-компонента вектора импульса в заданном объеме равна DxDuDx (drV ^ d^).
- Теперь подставим полученное выше выражение в выражение (3.10). Разделите все члены результирующей зависимости на Dx, Dx, Dx, а затем переместите до предела, поскольку Dx, Dx и Dx стремятся к нулю, чтобы получить X-компоненту уравнения движения. Аналогично можно найти компоненты движения по осям y и X. — ^- P » p = — (^- Р ₽^ y y + — ^ — Р ^ + + ^ ^ РЛ)• ⁾ аГ ^ = — (а? Х’Л +^ ^ № ^ ^ +〜 (3.16) стоимость оспа, ПГ«, ростом Р0.Такой. Свободного падения компонентов увеличивает η 1 стр. В одном компоненте Массовое разведение вектор ускорения вектор д / ДХ, д / ду, Д / ДГ- (Z.
I-(ZLb)-удобно есть [y-roo] , что произведение roo и m числа 1 не может быть рассмотрено, что первоначальная физическая интерпретация была дана в разделе (y-ro) продукта (y-ro), где отображается скорость потери массы G объем, vel1 [y-roo] представляет объем в единицах скорости. Используйте элементы и следующие формы: Ускорение движения под действием силы, сравнение движения, выраженного в объемных элементах. То есть это формула 2-го закона Ньютона. Масса X X ускорение=сумма forces.
Из вышеприведенных уравнений следует, что безразмерные составляющие скорости и безразмерные давления в обоих случаях являются одними и теми же функциями безразмерных координат и критерия Рейнольдса. Людмила Фирмаль
Легко проверить баланс Движение движения приводит к соотношению, полностью равному второму закону Ньютона. Обратите внимание, что 2 формы обозначения равны Уравнениям движения (3.17) и (3.19) соответствуют 2 формы записи непрерывных уравнений (3.6) и (3.8).в каждом из этих случаев первая форма записи является результатом составления баланса объемных элементов, зафиксированных в пространстве, а вторая-описанием изменений, происходящих в объемных элементах, которые следуют за движением жидкости.
Уравнение (3.14)- Окружающая среда, движение Выяснить Для получения профиля скорости необходимо заменить формулу тангенциального и нормального напряжений функцией градиента скорости и физико-химических свойств жидкости. для Ньютона Жидкость, эти выражения будут*. (3.20 утра)) (3.21) (3.22) Ч(^ + ^-) > Формула (3.20)-(3.25) дана без доказательств, поскольку соответствующий вывод является достаточно трудоемким[4, 5].Эти формулы являются более общей формулировкой ньютоновской вязкости, чем уравнение (1.2), которое может быть применено в случае сложных течений, в которых жидкость движется во всех направлениях.
Если жидкость движется в направлении оси x между двумя пластинами, перпендикулярными оси y (см. рис. 1-1), r> x является функцией (3.20 а) только координаты Y сводятся к (3, / 5a)、 + м[^ ^-+ ^)] + ^ [«(。5 -/ -^)] +и | + Р »» (3-27) + * [- φ+ *) 1 + » * * — b(?- о)] + п» «(3-28) Равномерно отражают непрерывность, граничные и начальные зависимости плотности Зеня.: П-757 — = — УР +tsu2o+ ры (3.29) Компоненты этого уравнения в декартовых координатах описаны на стр. 87[формула (P-g)-(P-e)].Соотношения (3.29)-это знаменитое уравнение Навье-Стокса, впервые полученное французским ученым Навье в 1822 году на основе нескольких гипотез о молекуле.
Смотрите также:
| Уравнения сохранения для изотермических систем | Уравнение механической энергии |
| Уравнение неразрывности | Уравнения сохранения в криволинейных координатах |

