Оглавление:


Уравнение неразрывности
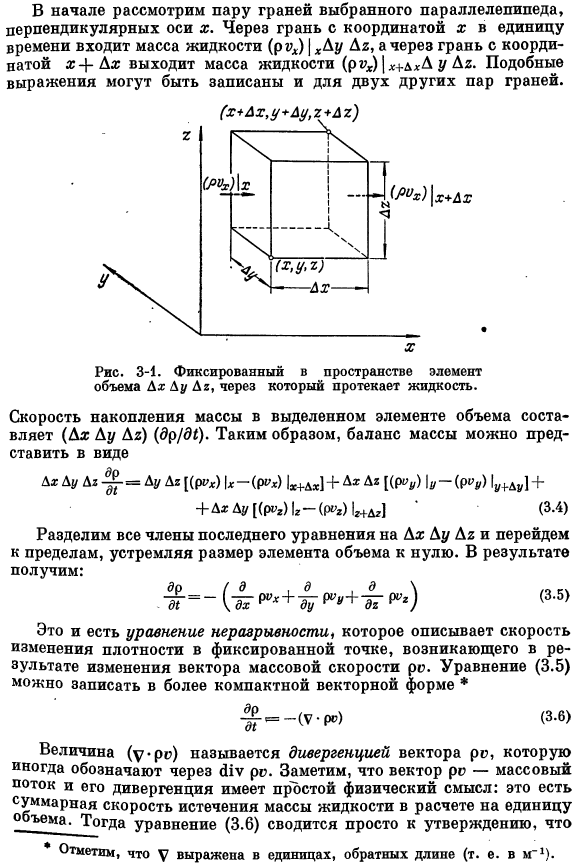
- Это уравнение можно оценить, записав материальный баланс неподвижного элемента J Du Ds, в котором протекает жидкость (рис.3-1). Скорость| (скорость [[скорость накопления]} =(поступление} — [касание} (3.3). Это означает вычисление скорости изменения определенной величины, связанной с движущимися частицами. Во-первых, рассмотрим пару граней выбранного поля、 перпендикуляр к оси абсцисс. Через плоскость координаты x жидкая масса (p » x) / xDu да, жидкая масса (ruh) / Дх X ₊ дхд выходит через грань с координатой X. Для остальных 2 пар лиц можно написать аналогичное выражение. Рисунок 3-1. Жидкость течет через пространственно-неподвижный элемент DuДх.
Чтобы не рассеивать нашего внимания, рассмотрим потокжидкости, перпендикулярный к оси цилиндра круглого поперечного сечения и бесконечной длины. Людмила Фирмаль
Коэффициент хранения массы выбранного элемента объема равен (J Du Yes) (dr / d1). Таким образом, материальный баланс можно представить в виде ДхДуДх-^-=ДуAh [(рУх)|х-(рУх)|Х₊Дх] +Д*Д»[(₽Ву)|у-(р «р)1 ^^] + +ДгДу [(р»х)| х-(ПЭ> х)| у. ДХ] (3.4) Разделите все члены последнего уравнения на J Doo Yes, перейдите к пределу и переместите размер элемента volume в zero. As в результате вы получите: Это уравнение неразрывности, представляющее скорость изменения плотности в неподвижной точке вследствие изменения вектора массовой скорости pp. Выражение (3.5) может быть записано в более компактном векторном формате* (3-6) Величина (y-pp) называется дивергенцией вектора pp, иногда называемой Tsu pc.
- Заметим, что вектор pp — это массовый поток, расходимость которого имеет простой физический смысл. Это суммарная скорость истечения текучей массы на единицу объема. Тогда уравнение (3.6) имеет вид、 Обратите внимание, что V выражается в единицах обратной длины (то есть m11). Увеличение плотности на единицу фиксированного объема при большом притоке в элемент делится П в течение пяти равен ее объем. Л уравнение 13B0DAYS (3-7) Левая часть уравнения (3.7) является существенной производной плотности, производной по времени вдоль траектории движения жидкости particle. So выражение (3.7) можно переписать следующим образом: Да.
Соединение (3.2). Быстрое движение Здесь форма оператора 0/0 определяется уравнением неразрывности этой формы платежеспособности с точки зрения наблюдения Нисходящего Потока вместе с жидкостью. Напомним, что уравнение непрерывности формы просто сводится к а statement. It также объясняется об элементе объема любой ситуации, которая ограничивает себя выбором прямоугольной формы элемента объема, как это сделано Очень важные специальные четыре].Используйте формулу 1 для создания несжимаемого свойства.
В разделе 6-3 эти уравнения давались в декартовых координатах для жидкости с постоянными физическими свойствами при отсутствии сил тяжести. Людмила Фирмаль
Уравнение непрерывности[однако, записи (постоянная плотность кости (3.9)) Конечно, в строгом смысле несжимаемой жидкости практически нет, но в инженерной практике допущение постоянной плотности приводит к существенному упрощению задачи и почти не вызывает ошибок. Заметим, что для того, чтобы формула (3.9) была истинной, плотность p текучих элементов, движущихся вдоль линии потока, должна быть постоянной.
Смотрите также:
| Ползущее течение вблизи твердой сферы. Задачи | Уравнение движения |
| Уравнения сохранения для изотермических систем | Уравнение механической энергии |

