Оглавление:





Ползущее течение вблизи твердой сферы. Задачи
- Удаление каталитических частиц дымовым газом, а) оценить максимальный диаметр мелких сферических частиц катализатора, уносимых вместе с дымовым газом оборудования для жидкофазного разложения при следующих условиях. Динамическая вязкость газа p. = 0,026 СР; плотность газа pg = 7,2-10 «* г-см -⁸; плотность pk = 1,2 г-см⁸ для отдельных частиц катализатора. Ответ записывается в микронах(1 МКК= 10 » ⁸m). b) разрешено ли использовать метод Стокса в случае Ответ: ОТА= 110 мкм; Ке = 0,93. 2-2. Гравитационный поток пленки является дополнительным выводом.
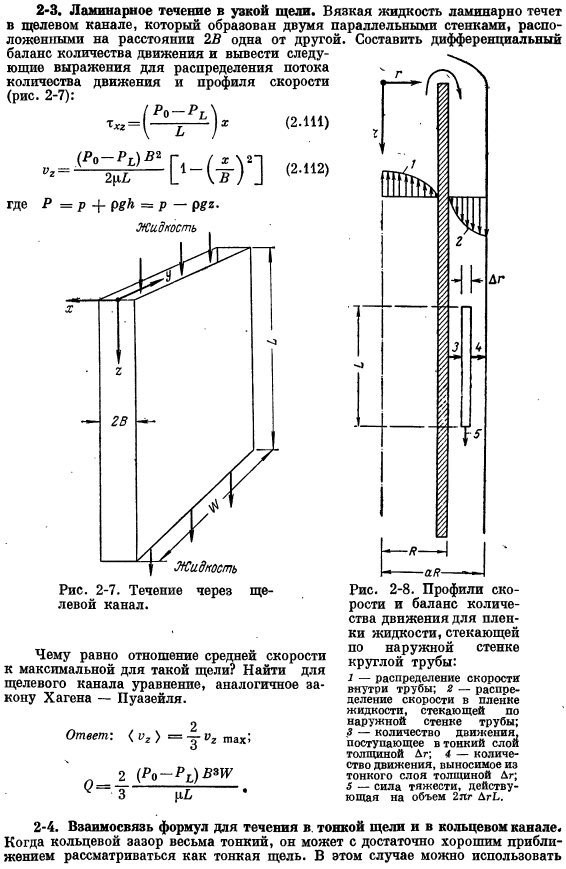
Выведите уравнение профиля скорости и средней скорости путем размещения координат начала координат^на стенке твердого тела, x = 6 на свободной поверхности пленки. Распределение скорости в этом случае указывает на то, что его можно найти из уравнения Равно максимальному значению; щелевой конус Пирог? В аналогичном порядке находим Это можно считать узким gap. In (2.113) I (Рв-Р₁₁) П * ^ Шестой подставьте выражение (2.71) вместо эквивалентной суммы x(1-е), а после получения выражения2 в виде степенного ряда, указывающего, что вы получите тот же результат. Эта операция включает в себя расширение Тейлора (2.114) А затем деление многочленов.
Однако позже будет показано, что требуется только приблизительное знание уравнений, так как в противном случае нельзя произвести удовлетворительный анализ также и каким-нибудь другим методом. Людмила Фирмаль
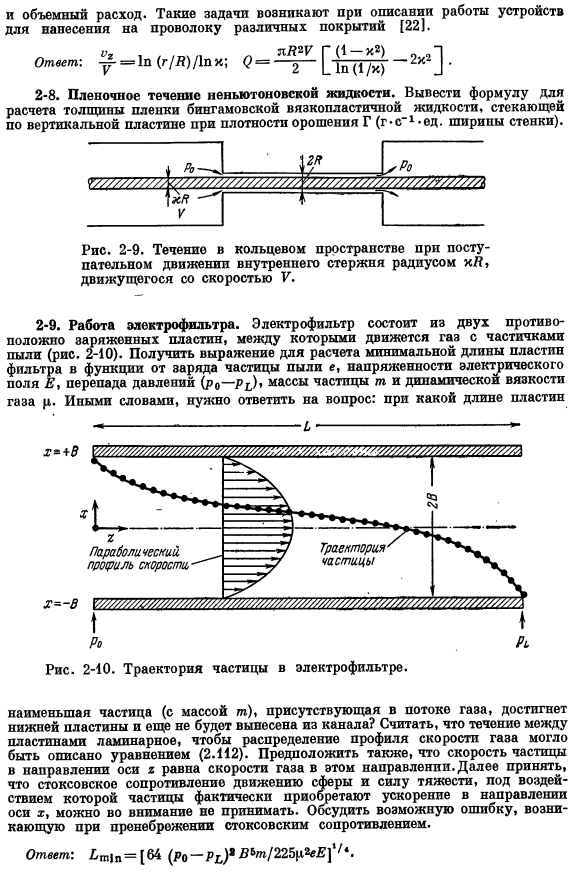
Первый член этого ряда эквивалентен формуле (2.113).В выводе используются первые 4 члена ряда Тейлора (2.114). 2-5.Ламинарное течение пленки жидкости вдоль наружной стенки круга pipe. In в экспериментах по поглощению поток вязкой жидкости поднимается по небольшой круглой трубе и протекает через ее внешнюю стенку (рис.2-8).Уравновесьте импульс тонкого слоя, показанного на рисунке, и толщину пленки жидкости. При редактировании баланса обратите внимание, что стрелки, соответствующие»входящему в слой»и»выходящему» импульсу, всегда соответствуют положительному направлению координаты R.
Как выяснилось в рассматриваемом вопросе, сумма а) указывает, что распределение скоростей в пленке (если игнорировать конечный эффект) выражается формулой: в)1?Если толщина пленки очень тонкая, установите, что результат, полученный в пункте»в», упрощен до соотношения (2.20). 2-6.Используя неньютоновское течение в трубе, а) модель Оствальда-Вейля (степенной закон Беки), мы получаем аналог модели Хагена-пуастиля equation. In вывод, прежде всего, необходимо убрать знак абсолютной величины.
- Поскольку производная1ig / Lr отрицательна везде в потоке в трубе, степенной закон в этом случае может быть выражен следующим образом: Кратко объясните смысл преобразований, приведших к возникновению связи (2.116). б) получаем уравнение объемного расхода жидкости в трубе модели Эллиса[эталонное уравнение (1.11)]: — =Рота, г +Ф11t «я-«(2.117) 2-7.Электрический ток Скорость И объем потока. Такие проблемы возникают при описании работы устройств, нанесенных на провода с различными покрытиями [22]. Операция 2-9.Работа электрофильтра.
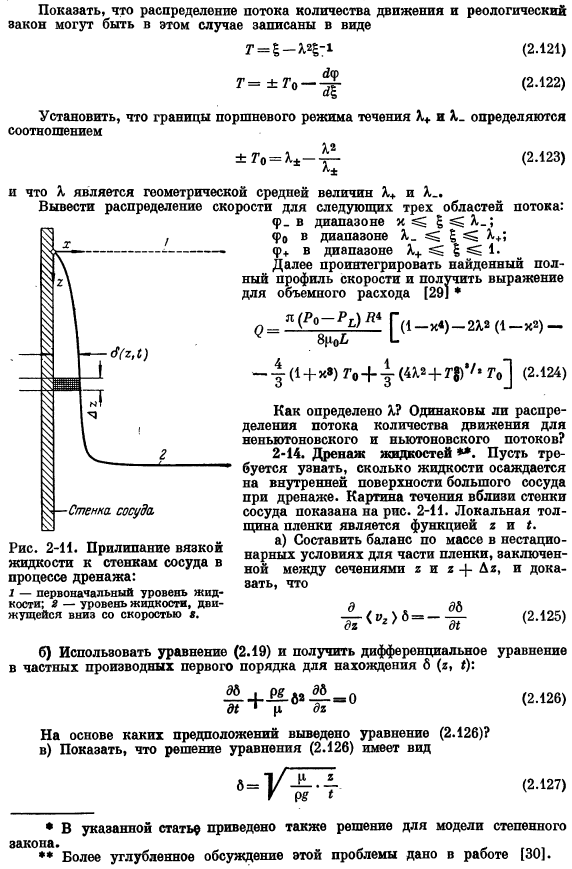
Электрофильтр состоит из двух пластин, заряженных в противоположных направлениях, между которыми перемещается пыль Ha(рис.2-10).Сделать маленький расчет Напряжение ааименпая частица (масса т), присутствует В этом направлении. Далее примите и расставьте приоритеты ускорения в направлении■b. обсудите возможные ошибки и создайте сопротивление. Ответ: Дт|П= [64(р₀—рь)»В5т/225р»» я)»/*. Предыдущий пункт l-Интеграл, полученный уравнением Rab nth /Я= mт/где (где =(,,, / /2г-стена при R=)) и перепишите Интеграл (2.119) Как графически построить формулу (2.120) зависимости[m] 2-12.Зависимость представляет собой профиль скорости кольцевого капельницы и зазора.
По своему опыту автор считает, что наиболее эффективным и верным путем получения ответа на этот вопрос является метод, который основывается на дифференциальных уравнениях, описывающих процесс и -преобразование их в безразмерные дифференциальные уравнения. Людмила Фирмаль
Распределение скорости (2.68) кольцевого канала указывает, что оно будет таким же, как и распределение скорости (2.112) в потоке щелевого канала. Обратите внимание на подстрочные Буквы в разделе 2.4(см. стр.
Используйте результаты в Примере 2-2 для расчета объемного расхода, когда вязкая пластическая жидкость Бингема течет через кольцевой канал, и введите следующее безразмерное число чисел: Импульс 7, безразмерный поток= 2М, переменные XB1 (п,-п.) я; реология безразмерного параметра Т =2t₀G/(₀—ПБ) я; безразмерной скоростиР = [2П Д /(П-ПБ) Р») безразмерный радиус координат 5 г / л Режим * Решение модели права должно быть также описано в указанной статье* * Более подробное обсуждение этого вопроса описано в[30]. Какие ограничения должны быть наложены на выражение результата?
В результате исследования полутентного превращения жира (или смазки) в круглой трубе была предложена следующая математическая модель[31]. (Т?- ) + ‘ (- Зг)» — ’ +» (2.128) Объемный поток Вам нужно будет найти формулу для this.
Смотрите также:
| Совместное течение двух несмешивающихся жидкостей | Уравнения сохранения для изотермических систем |
| Ползущее течение вблизи твердой сферы | Уравнение неразрывности |

