Оглавление:






Ползущее течение вблизи твердой сферы
- В предыдущем разделе решались некоторые простые задачи вязкого течения путем составления дифференциального уравнения импульса баланса. Во вступительной части этой главы мы подчеркивали, что такие методы анализа ограничены потоками, которые не являются турбулентными. Задачи, которые обтекают сферу, сопровождаются криволинейными линиями тока, поэтому их нельзя решить уже знакомыми методами. Тем не менее, учитывая важную роль технологии в процессе обтекания объектов в потоке, сейчас уместно вкратце обсудить этот вопрос issue. In в этом случае мы не пытаемся вывести формулу, которая соответствует распределению импульса, давления и потока.
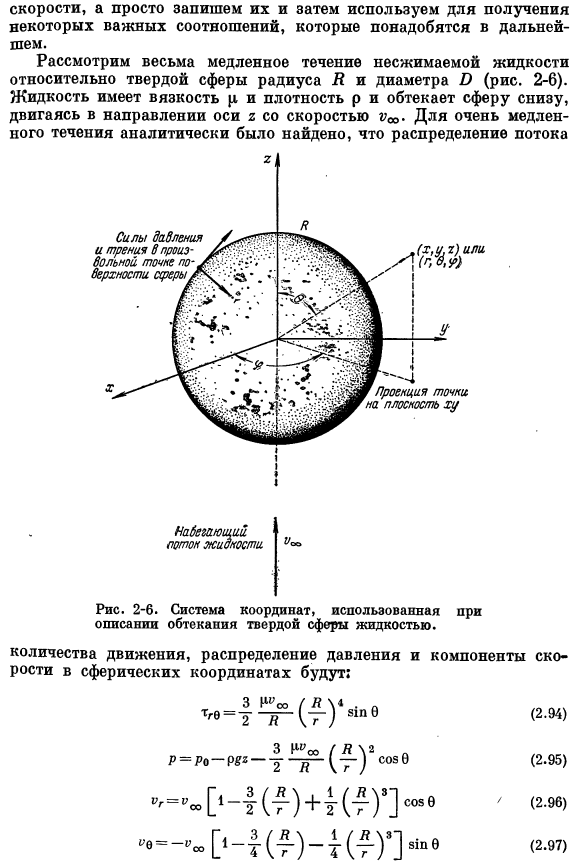
Посмотреть работы [17-191;более подробное обсуждение этого вопроса можно найти в монографии[20].Нестационарное движение сферы рассматривается в главе 7 настоящей главы. Течение сферы вокруг несетевой жидкости было изучено в работе [21]. Используйте его, чтобы ускорить и записать их, а затем получить некоторые важные отношения, которые вам понадобятся в будущем Рассмотрим очень медленное течение несжимаемой жидкости по сравнению с твердыми сферами с радиусом D и диаметром O (рис.2-6).Жидкость имеет вязкость и плотность Р, течет снизу вокруг шара. 2-6.Система координат, используемая для описания потока жидкости вокруг твердой сферы.
Наиболее важной и трудной частью анализа является нахождение не формы параметров, а их числа, которые полностью описывают рассматриваемый процесс. Людмила Фирмаль
Компоненты импульса, давления и скорости сферических координат являются: Р = Ро-р / г-4 ^(^)2CO36(2.95) (2.97) (2.95) секция p давление секции 2= 0 far-p ^ 2-это эффект (1 эффект) веса жидкости. Термины, содержащие » «, появляются после сферы из-за жидкости. Соотношение справедливо только для «ползучего в данном случае«.Наблюдается величина-lr / p, примерно меньше 0,1.Область течения характеризуется существенным отсутствием вихреобразования сферами. Что распределение скорости соотвествует поверхности sphere. In кроме того, указывается, что значение будет достигнуто на достаточном расстоянии от sphere.
Кроме того, очевидно, что распределение давления превышает затухание на расстоянии P =p₀-p # 3.Поверхность шара. Таким образом, рассматриваемое уравнение фактически удовлетворяет граничным условиям r = H и r=°°. Теперь рассчитаем суммарную силу, действующую с жидкой стороны сферы. Эта сила обнаруживается путем интегрирования поверхностных нормальных и касательных компонентов Нормальная интеграция сил. Каждая точка на поверхности сферы имеет силу р на единицу площади, которая действует на твердое тело в направлении, перпендикулярном поверхности.
Составляющая этой силы вдоль оси 2 равна-p cos0.Указанное локальное значение силы умножается на размер действующей фундаментальной области (Я⁸зт0 40 ₽ 4) и интегрируется по всей поверхности сферы для получения результирующей силы в направлении оси (G).: (2.98) Распределение давления на поверхности сферы выглядит следующим образом: (£2.99)) Присвойте это выражение выражению (2.98). Интеграл с pn аннигилируется, а Интеграл с-rcB cos 0 дает жидкости силу удерживать твердую сферу, в то время как Интеграл со скоростью определяет «сопротивление формы». таким образом, в конечном итоге это будет выглядеть так: / ’Я = yPY ’ РВ + 2lry1> о(2.100) Тангенциальная сила integration.
- В каждой точке на поверхности сферы имеются также касательные (напряжения-м, в, приложенные в тангенциальном направлении). Этот стресс является、 Единица сферы действует на поверхность доски с координатами 0.Величина 2 составляющих этой силы на единицу поверхности равна (- m, e) (- 81n 0).Если вы умножите указанное значение на D 31 n 0 0 0 и интегрируете его со всей поверхностью сферы, вы получите силу в направлении оси X. P₁₁= г г(м, е | g_v s1n 6)я 0(2.101) Распределение напряжения сдвига на поверхности сферы следует формуле (2.96): Подставляя эту формулу в интеграл от формулы (2.101), можно найти «сопротивление трения»*.
Таким образом, сила Р, действующая на сферу со стороны жидкости, может быть выражена как сумма сил, определяемых формулами(2.100) и (2.103). = = ЛЯЛЯ » Р » «» + 2яряя1 > EO + 4яряя » ОО; (2.104) Ваюцаясвла) Гаерфорый Нветреияя) = =ЛЛ «PRPR + 6lph1 > ₀₀ (2.105) Первый член в правой части уравнения (2.105) характеризует несущую силу, а второй член появляется в результате движения жидкости вокруг sphere. In в следующем представлении было бы полезно представить эти 2 члена с помощью P (сила, которая существует без движения жидкости) и Pk (сила, связанная с движением жидкости, то есть компонент „движение“), respectively.
Остается только одна возможность: положиться на эксперимент и обобщать результаты путем анализа размерностей. Людмила Фирмаль
В случае выполнения описанной задачи указанные силы являются: / ’, = Юля Р? (2.106)) Як бя^(2.107) Рост, ПА „коммуналку“ (а потому лучше „явление“ и » коммуналку」 Формула(2.107) известна как закон Стокса. Этот закон применим к описанию движения коллоидных частиц под действием электрического поля в теории седиментации. Порядка 0,1 (вычисляется по диаметру сферы). При He = 1 сопротивление, определяемое законом Стокса, примерно на 10% ниже истинного сопротивления.
Поведение одной и той же модельной системы при большом числе Рейнольдса описано в главе 6.Приведенная выше задача показывает, что гидродинамические задачи должны быть сформулированы в более общем виде, чтобы охватить случай криволинейного обтекания. Этот подход разработан в главе 3. Где P-радиус сферы, ptv-ее плотность, 1> kOn — «конечная скорость».Решите уравнение(2.108) [Дар падения в вязкую жидкость с самого начала ускоряется, пока не достигнет ГРУ, должно быть равно нулю.
Сила представляет собой твердую сферу в направлении ее падения, а несущая сила вследствие движения жидкости действует в противоположных направлениях. 6p / и> Конья 2Х2 (RT » — RI 9con (2.108) Плотность жидкости является оптимальным способом、 (2.109) Найденные результаты действительны только в том случае, если зпаченпях Огойе п / п меньше-шпх равен 0,1.
Смотрите также:
| Течение в кольцевом канале | Ползущее течение вблизи твердой сферы. Задачи |
| Совместное течение двух несмешивающихся жидкостей | Уравнения сохранения для изотермических систем |

